The ratio of the time periods of small oscillation of the insulated spring and mass system before and after charging the masses is

A

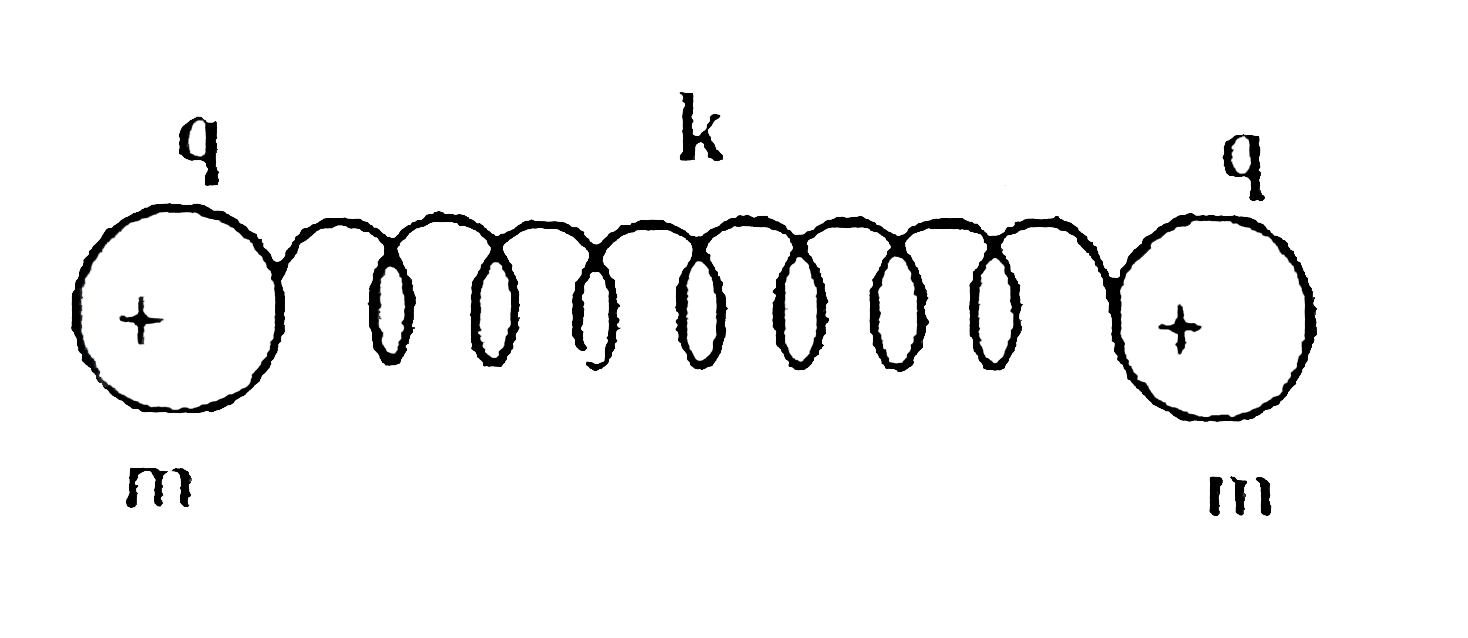
$\geq 1$

B

$> 1$

C

$\leq 1$

D

$= 1$

Video Solution

Text Solution

Verified by Experts

In equilibrium of the charged small bodies $\frac{1}{4 π ε_{0}} \frac{q^{2}}{{(l_{0} + x_{0})}_{0}^{2}} = k x_{0}$ where $x_{0}$ is the elongation in the spring in equilibrium.
Let a further small elongation of $x$ is given to the spring.
Then net restoring force on any of the charged particle is given by,
$F = - [k (x_{0} + x) - \frac{1}{4 π ε_{0}} \frac{q^{2}}{{(l_{0} + x_{0} + x)}_{0}^{2}}] = - k x$ . Since $x < < x_{0}$
$\Rightarrow a = - \frac{2 k}{m} x$ As $F = μ a$ , where reduced mass $μ = \frac{m \times m}{m + m} = \frac{m}{2}$
$\Rightarrow a = - ω^{2} x$ ,
Hence $ω = \sqrt{\frac{2 k}{m}} \Rightarrow T = 2 π \sqrt{\frac{m}{2 k}}$
In absence of charge, $T_{0} = 2 π \sqrt{\frac{m}{2 k}}$
Therefore $\frac{T}{T_{0}} = 1$
$∴ (D)$

Updated on:21/07/2023

|

Class 12 PHYSICS ELECTRIC CHARGES AND FIELDS

Similar Questions

Recommended Questions

Home
Ask Doubt
Profile