In the figure shown, mass of the plank is m and that of the solid cylinder is 8m. Springs are light. The plank is slightly displaced from equilibrium and then released. Find the period of small oscillations (in seconds) of the plank. There is no slipping at any contact point. The ratio of the mass of the plank adn stiffness of the spring i.e., $\frac{m}{K} = \frac{2}{π^{2}}$

Video Solution

Text Solution

Verified by Experts

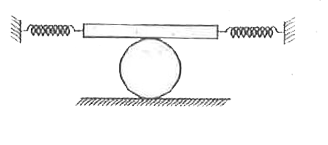
If the plank is displaced slightly by x towards left, then

$2 K x - f_{1} = m a_{2}$ …(i)
$f_{1} + f_{2} = 8 m a_{1}$ …(ii)
$τ_{c m} = l_{c m} α$

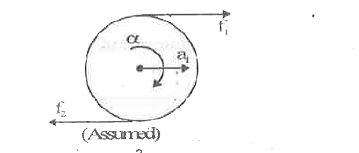
or $(f_{1} + f_{2}) R = \frac{(8 m) R^{2}}{2} α$
$(f_{1} + f_{2}) = \frac{(8 m) a_{1}}{2}$ ...(iii)
From (ii) and (iii),
$2 f_{1} = (8 m) \times \frac{3 a_{1}}{2}$
or $f_{1} = (8 m) \times \frac{3 a_{1}}{4}$
and $f_{2} = - 2 m a_{1}$
Hence $f_{2}$ will be in forward direction.
Also, for no slipping, at the point of contant between plank and cylinder
$2 a_{1} = a_{2}$ ...(iv)
$f_{1} = (8 m) \times (\frac{3 a_{2}}{8}) = (3 m) a_{2}$ ...(v)
from (i) and (v)
$2 K x - (3 m) a_{2} = m a_{2}$
$a_{2} = \frac{2 K}{4 m} x$
or $(\frac{- d^{2} x}{{d t}^{2}}) = (\frac{2 K}{4 m}) x$
or $\frac{d^{2} x}{{d t}^{2}} = - (\frac{2}{4} \times \frac{π^{2}}{2}) x$
$or ω^{2} = \frac{π^{2}}{4}$
or $ω = \frac{π}{2}$
or $\frac{2 π}{T} = \frac{π}{2}$
or T = 4 seconds.

Updated on:21/07/2023

|

Class 12 PHYSICS SIMPLE HARMONIC MOTION

Similar Questions

Recommended Questions

Home
Ask Doubt
Profile