A plank of mass M is placed on a smooth hroizonal surface. Two light identical springs each of stiffness k are rigidly connected to structs at the ends of the plank as shown. When the spring are in their unextended position the distance between their free ends is 3l. a block of mass m is placed on the plank and pressed aganist one of the springs so that it is compressed by l. To keep the blocks at rest it is connected to the strut by means of a light string, initially the syetem is at rest. Now the string is burnt.

Maximum displacement of plank is:
mlm+M
5mlm+M
3mlm+M
2mlm+M
The correct Answer is:B
(1) CM remains at rest, block moves 5t on plank when system comes to rest
−m[5l−Δx]+MΔx=0,Δx=5mlm+M
(2) In CM frame 12(m.Mm+M)v2m/M=12kl2
Vv/M=√(M+mMm)kl
(3) Consider motion of block w.r.t. plank
aM=kxM right ward, F=−(kx+maM) or
d2xdt2=(kmx+aM)=−k(1M+1M)xω2=π2√Mm(m+m)k
Time to get the spring relaxed is t1=π2√MmM+mk
Time taken by block to travel 3l between springs
=3lvm/M=3l√k(M+m)Mml
Time period of oscillation of block
=2⎡⎢
⎢⎣2t1+3l√k(M+m)MmMml⎤⎥
⎥⎦=(2π+6)√Mmk(M+m)
Topper's Solved these Questions
- OSCILLATIONSBook:NARAYNAChapter:OSCILLATIONSExercise:Passage-VII
Explore 1 Video
- OSCILLATIONSBook:NARAYNAChapter:OSCILLATIONSExercise:Passage-VIII
Explore 1 Video
- OSCILLATIONSBook:NARAYNAChapter:OSCILLATIONSExercise:LEVEL-VI
Explore 1 Video
- NEWTONS LAWS OF MOTIONBook:NARAYNAChapter:NEWTONS LAWS OF MOTIONExercise:PASSAGE TYPE QUESTION
Explore 6 Videos
- PHYSICAL WORLDBook:NARAYNAChapter:PHYSICAL WORLDExercise:C.U.Q
Explore 10 Videos
Similar Questions
A wooden plank of mass 20kg is resting on a smooth horizontal floor. A man of mass 60kg starts moving from one end of the plank to the other end. The length of the plank is 10m. Find the displacement of the plank over the floor when the man reaches the other end of the plank.

View SolutionA wooden plank of mass 20 kg is resting on a smooth horizontal floor. A man of mass 60 kg starts moving from one end of the plank to the other end. The length of the plank is 10 m. Find the displacement of the plank over the floor when the man reaches the other end of the plank.

View Solution
Knowledge Check
A plank of mass M is placed on a smooth hroizonal surface. Two light identical springs each of stiffness k are rigidly connected to structs at the ends of the plank as shown. When the spring are in their unextended position the distance between their free ends is 3l. a block of mass m is placed on the plank and pressed aganist one of the springs so that it is compressed by l. To keep the blocks at rest it is connected to the strut by means of a light string, initially the syetem is at rest. Now the string is burnt.
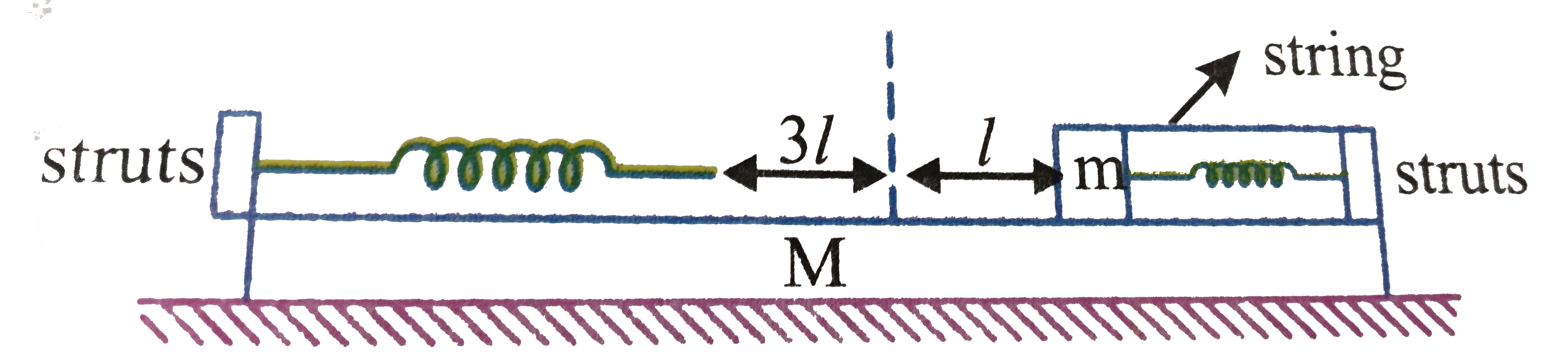
Time period of oscillation of block:A(2π+3)√2Mnk(M+m)B(π+6)√2Mnk(M+m)C(π+3)√Mmk(M+m)D(2π+6)√Mmk(M+m)According to the principle of conservation of linear momentum if the external force acting on the system is zero, the linear momentum of the system will remain conserved. It means if the centre of mass of a system is initially at rest, it will remain at rest in the absence of external force, that is, the displacement of centre of mass will be zero.
A plank of mass M is placed on a smooth horizontal surface. light identical springs, each of stiffness K, are rigidly connected to struts at the end of the plank as shown in Fig. When the springs are in their unextended position, the distance between their free ends is 3l. A block of mass m is placed on the plank and pressed against one of the springs so that it is compressed to l. To keep the block at rest it is connected to the strut means of a light string. Initially, the system is at rest, Now the string is burnt.
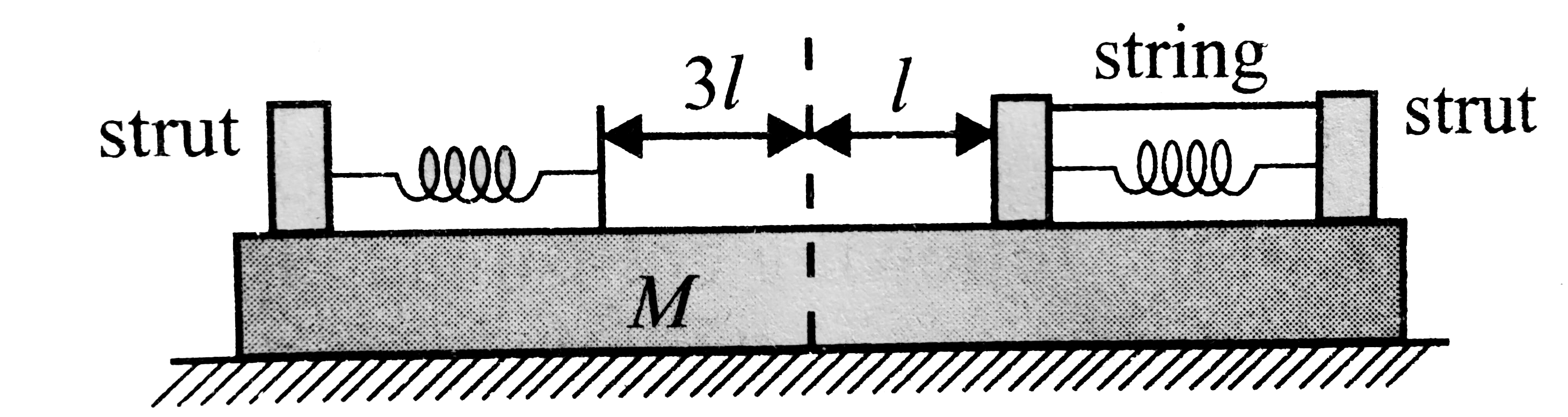
The maximum displacement of the plank isA5mlMB5mlM+mC3mlM+mD4mlM+mAccording to the principle of conservation of linear momentum if the external force acting on the system is zero, the linear momentum of the system will remain conserved. It means if the centre of mass of a system is initially at rest, it will remain at rest in the absence of external force, that is, the displacement of centre of mass will be zero.
A plank of mass M is placed on a smooth horizontal surface. light identical springs, each of stiffness K, are rigidly connected to struts at the end of the plank as shown in Fig. When the springs are in their unextended position, the distance between their free ends is 3l. A block of mass m is placed on the plank and pressed against one of the springs so that it is compressed to l. To keep the block at rest it is connected to the strut means of a light string. Initially, the system is at rest, Now the string is burnt.

The maximum velocity of the plank isA√Km(M+m)lB√k(M+m)lC√KmM(M+m)lD√kMm(M+m)l
A plank of mass M is placed on a rough horizontal force F is applied on it A man of mass m rens on the plank find the acceleration of the man so that the plank does not move on the surface . The coefficent of friction between the plank and the surface is μ Assume that the man does not slip on the plank

View SolutionA thin but very large plank of mass 2 m is placed on a horziontal smooth surface. A solid cylinder of mass m and radius r is given only translational velocity v0 and gently placed on the plank as shown in the figure. The coefficient of kinetic friciton between the plank and the cylinder is μ.

View SolutionA block of mass m, lying on a smooth horizontal surface, is attached to a spring (of negligible mass) of spring constant k. The other end of the spring is fixed, as shown in the figure. The block is initally at rest in its equilibrium position. If now the block is pulled withe a constant force F, the maximum speed of the block is :

View SolutionAccording to the principle of conservation of linear momentum if the external force acting on the system is zero, the linear momentum of the system will remain conserved. It means if the centre of mass of a system is initially at rest, it will remain at rest in the absence of external force, that is, the displacement of centre of mass will be zero.
A plank of mass M is placed on a smooth horizontal surface. light identical springs, each of stiffness K, are rigidly connected to struts at the end of the plank as shown in Fig. When the springs are in their unextended position, the distance between their free ends is 3l. A block of mass m is placed on the plank and pressed against one of the springs so that it is compressed to l. To keep the block at rest it is connected to the strut means of a light string. Initially, the system is at rest, Now the string is burnt.
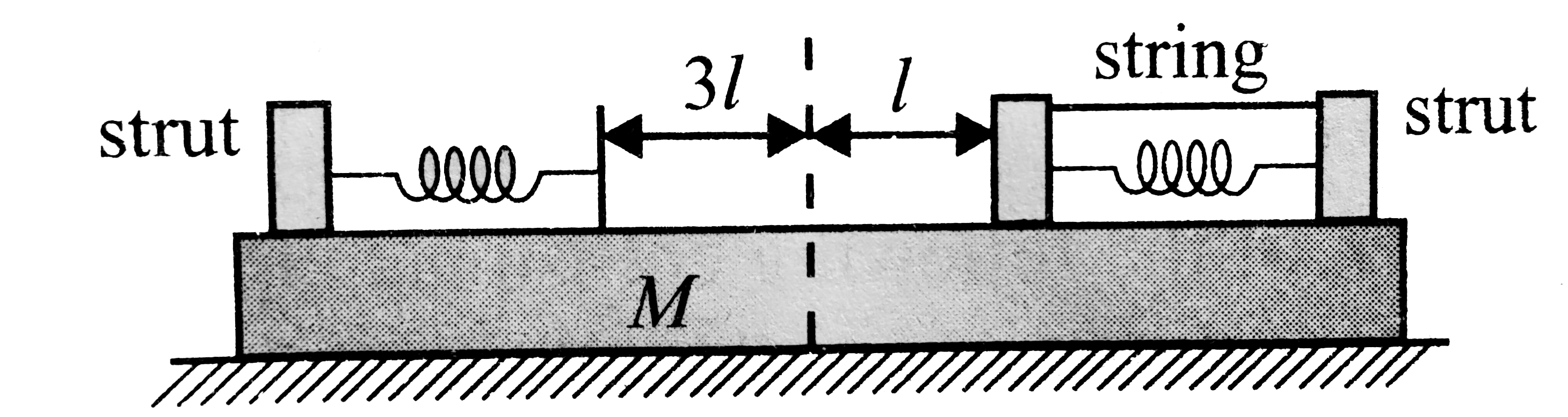
The maximum kinetic energy of the block m is
View SolutionA plank of mass 4m is placed on a smooth horizontal surface and a spring of force constant k is attached to the plank, whose other end is fixed on a block of mass m placed over tha plank. All surface are smooth. A bullet of mass m moving with horizontal velocity u strikes the block and gets embeded in it. Choose the correct option for subsequent motion :
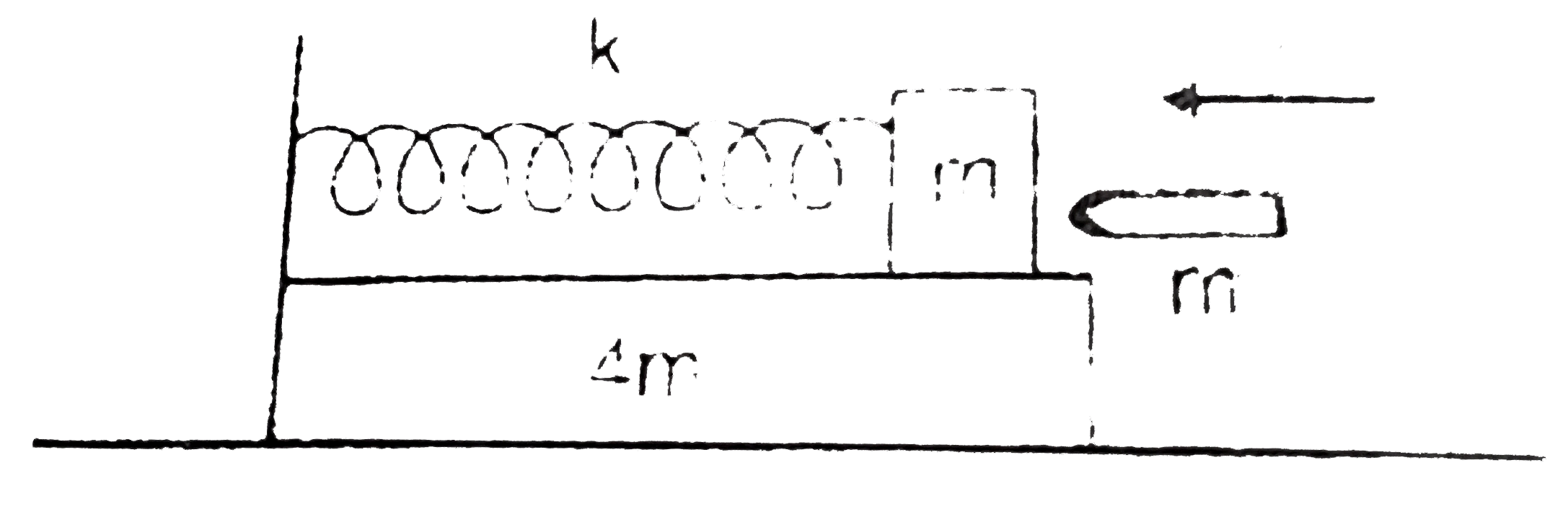
View Solution

