A plank of mass 4m is placed on a smooth horizontal surface and a spring of force constant k is attached to the plank, whose other end is fixed on a block of mass m placed over tha plank. All surface are smooth. A bullet of mass m moving with horizontal velocity u strikes the block and gets embeded in it. Choose the correct option for subsequent motion :
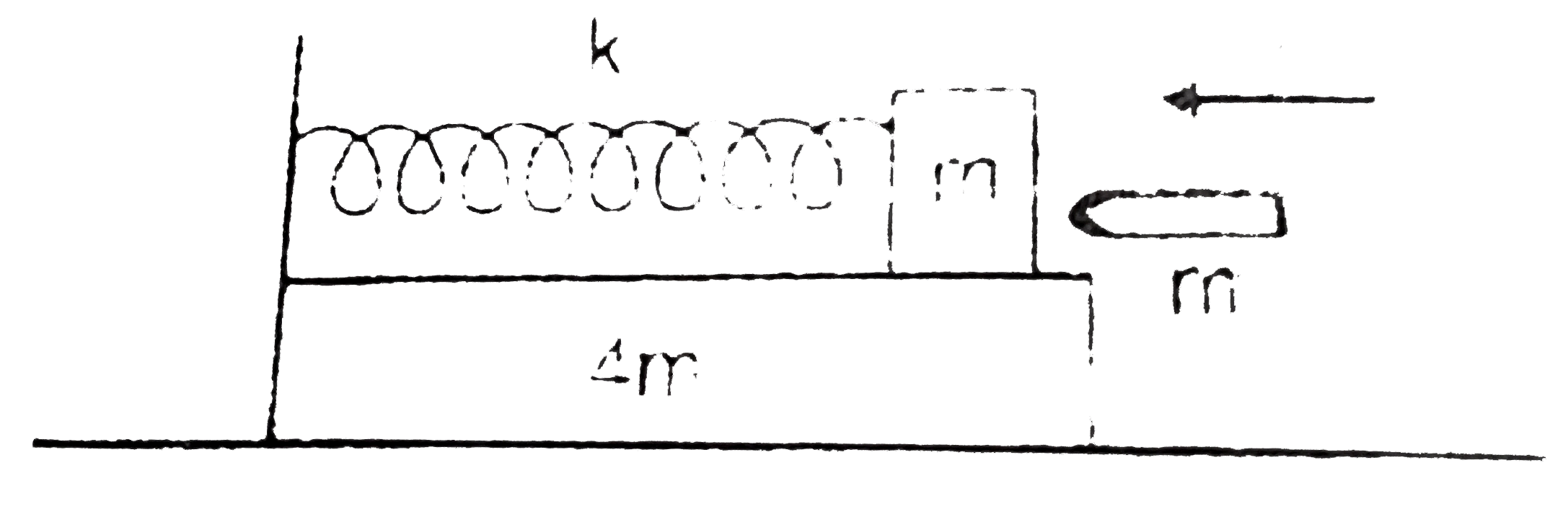
velocity of plane when spring gets compressed to maximum is u6
the maximum compression in the spring is √m3ku
the bullet will have velocity relative to plank at the instant of maximum compression
the force exerted by spring on plank will reach a maximum of √mu26k
The correct Answer is:A, B
mu=6mV
V=u6,122m(u/2)2=12(m+m+4m)V2+12kx2
⇒x=√m3Ku
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBook:RESONANCEChapter:DAILY PRACTICE PROBLEMExercise:DPP No.69
Explore 20 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCEChapter:DAILY PRACTICE PROBLEMExercise:DPP No.70
Explore 9 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCEChapter:DAILY PRACTICE PROBLEMExercise:DPP No.67
Explore 10 Videos
- CURRENT ELECTRICITYBook:RESONANCEChapter:CURRENT ELECTRICITYExercise:High Level Problems (HIP)
Explore 21 Videos
- ELECTRO MAGNETIC WAVESBook:RESONANCEChapter:ELECTRO MAGNETIC WAVESExercise:Exercise 3
Explore 27 Videos
Similar Questions
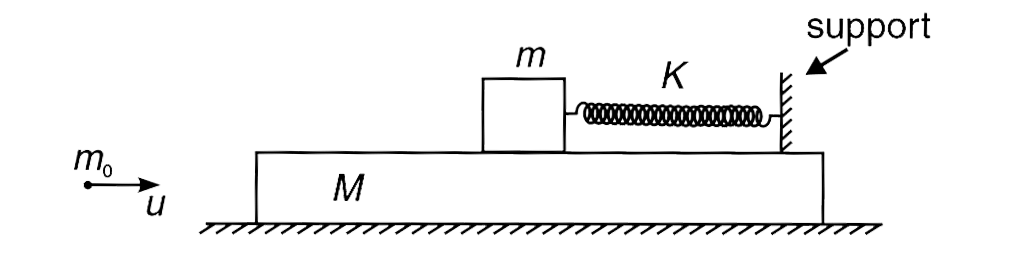
In the system shown in fig. block of mass M is placed on a smooth horizontal surface. There is a mass less rigid support attached to the block. Block of mass m is placed on the first block and it is connected to the support with a spring of force constant K. There is no friction between the blocks. A bullet of mass m0, moving with speed u hits the block of mass M and gets embedded into it. The collision is instantaneous. Assuming that m always stays over M, calculate the maximum extension in the spring caused during the subsequent motion.
K=8960N/m,u=400m/s
View SolutionA plank of mass M is placed on a rough horizontal surface and a contant horizontal force F is applied on it . A man of mass m runs on the plank find the range of acceleration of the man that the plank does not move on the surface is μ .Assume that the does not slip on the plank

View Solution
Knowledge Check
A bullet of mass m moving with a speed v strikes a wooden block of mass M & gets embedded into the block. The final speed is
A√MM+nVB√mM+nVCmM+nVDV2A block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. Two maximum compression in spring is
 A√2mkv0B√mk.v0C√mk.v0Dm2k.v0
A√2mkv0B√mk.v0C√mk.v0Dm2k.v0A plank of mass M is placed on a rough horizontal surface. A man m walks on the plank with an acceleration 'a' while the plank is also acted upon by a horizontal force F whose magnitude and direction can be adjusted to keep the plank at rest.
The coefficient of friction between plank and surface is μ. Choose the correct options.
 .AThe maximum value of F to keep plank at rest is ma+μ(M+m)gBThe minimum value of F to keep the plank at rest is ma−μ(M+m)gCThe direction of friction on ground due to plank will always be forwardDIf F=ma then friction on man due to plank is also F and friction between plank and ground will be zero
.AThe maximum value of F to keep plank at rest is ma+μ(M+m)gBThe minimum value of F to keep the plank at rest is ma−μ(M+m)gCThe direction of friction on ground due to plank will always be forwardDIf F=ma then friction on man due to plank is also F and friction between plank and ground will be zero
A block of mass m is placed at rest on a smooth wedge of mass M placed at rest on a smooth horizontal surface. As the system is released

View SolutionA block of mass M lying on a smooth· horizontal surface is rigidly attached ·to a light horizontal ·spring of spring constant k. The other end of the spring is rigidly connected to a fixed wall. A stationary gun fires ·bullets of mass m each in horizontal direction with speed υ0 one after other. The bullets hit the block and get embedded to it. The first bullet hits the block at t=0, the second bullent hits at t=2π√M+mk+2π√M+2mk and so on. The maximum comression in the spring after the nth bullet hits is :
View SolutionA man of mass m is standing on a plank of equal mass m resting on a smooth horizontal surface. The man starts moving on the plank with speed u relative to the plank. The speed of the man relative to the ground is

View SolutionA block of mass m is placed gently onto a long plank of mass M moving with a velocity v0 on a smooth horizontal floor. If friction is present between M and m :
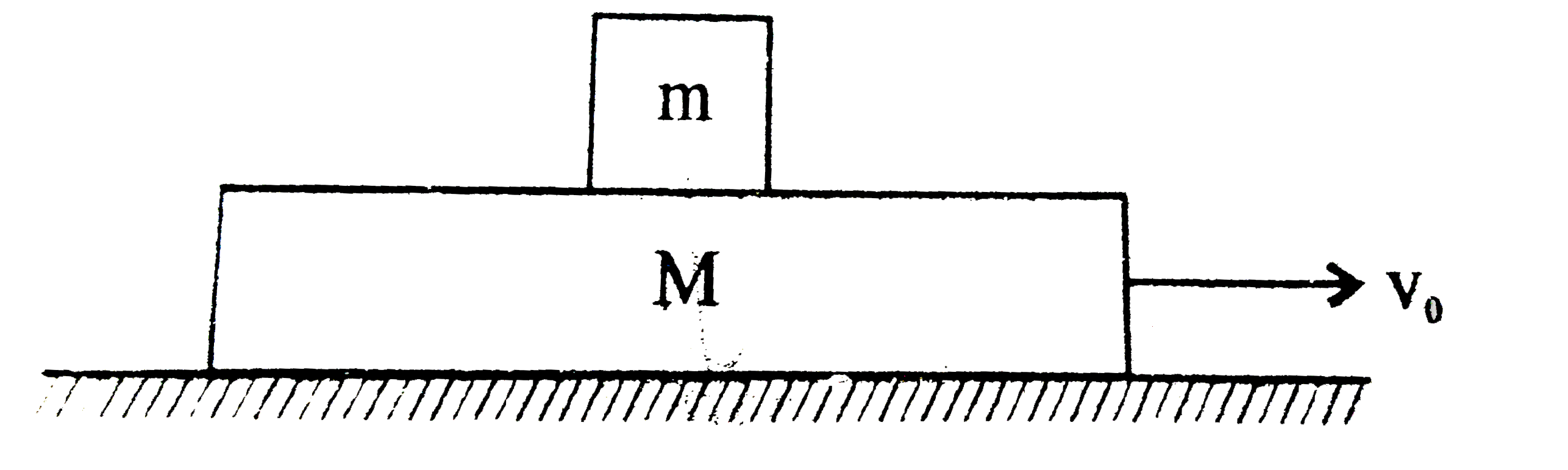
View SolutionA plank of mass M is placed on a smooth hroizonal surface. Two light identical springs each of stiffness k are rigidly connected to structs at the ends of the plank as shown. When the spring are in their unextended position the distance between their free ends is 3l. a block of mass m is placed on the plank and pressed aganist one of the springs so that it is compressed by l. To keep the blocks at rest it is connected to the strut by means of a light string, initially the syetem is at rest. Now the string is burnt.

Maximum displacement of plank is:
View Solution

