Three particles each of mass m can slide on fixed frictionless horizontal circular tracks in the same horizontal plane as shown in the figure. The coefficient of restitution being . Assuming that and are at rest initially and lie along a radial line before impact and the string is initially unstretched, then maximum extension in spring in subsequent motion

The correct Answer is:B
Velocity just after collision
….(A)
....(B)
from (A) & (B)
When maximum extension occur's then angular speed with rest to centre for mass & are same Using angular momentum conservation about centre of circle.
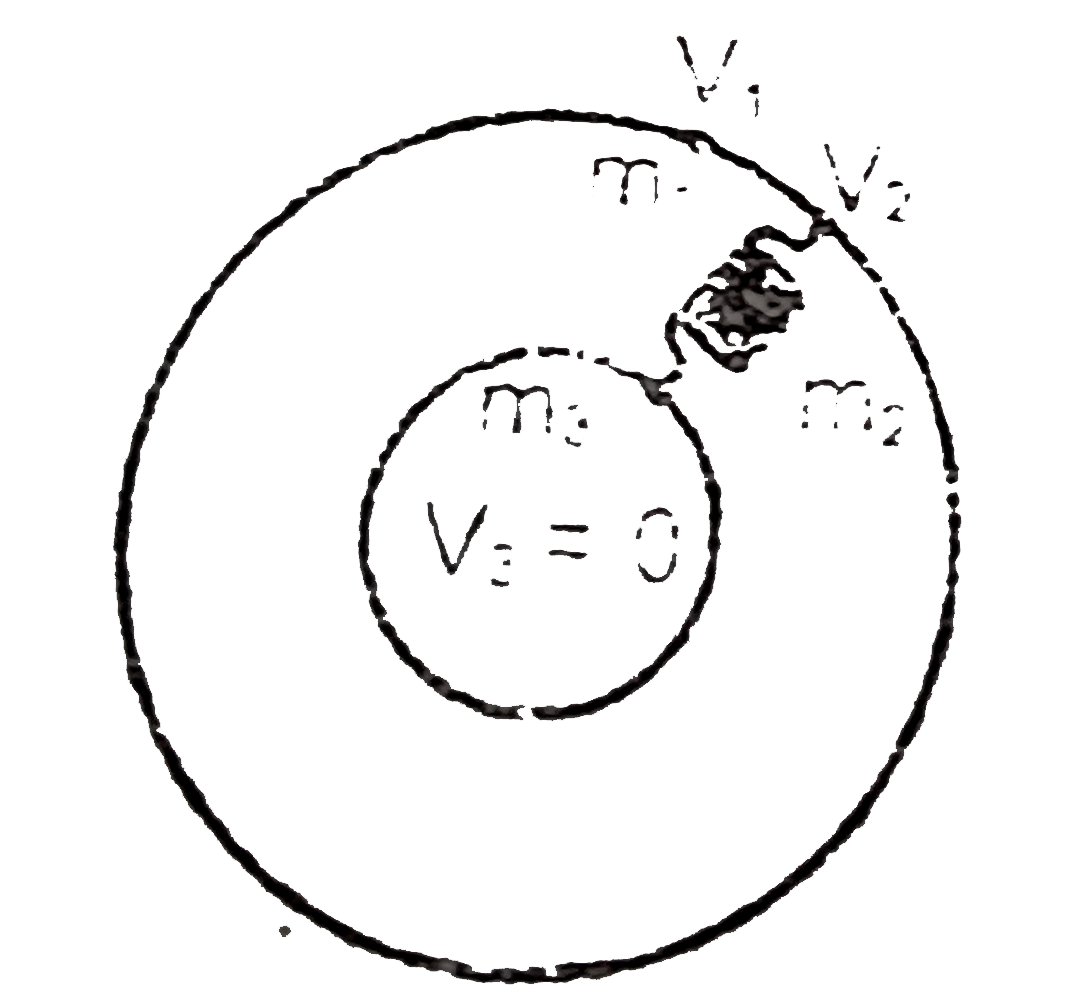
So velocity of
& velocity of
When extension is maximum using energy conservation
.
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.69
20 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.70
9 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.67
10 Videos
- CURRENT ELECTRICITYBOOK - RESONANCECHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)
21 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCECHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
Similar Questions
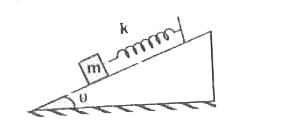
A block of mass m can slide along a frictionless inclined plane, is attached to a ideal spring of spring constant as shown in the figure. Find the period of its oscillation. (Frame of reference attached to the wedge is at rest)
View SolutionTwo blocks of masses m and M connected by a spring are placed on frictionless horizontal ground. When the spring is relaxed, a constant force F is applied as shown. Find maximum extension of the spring during subsequent motion.
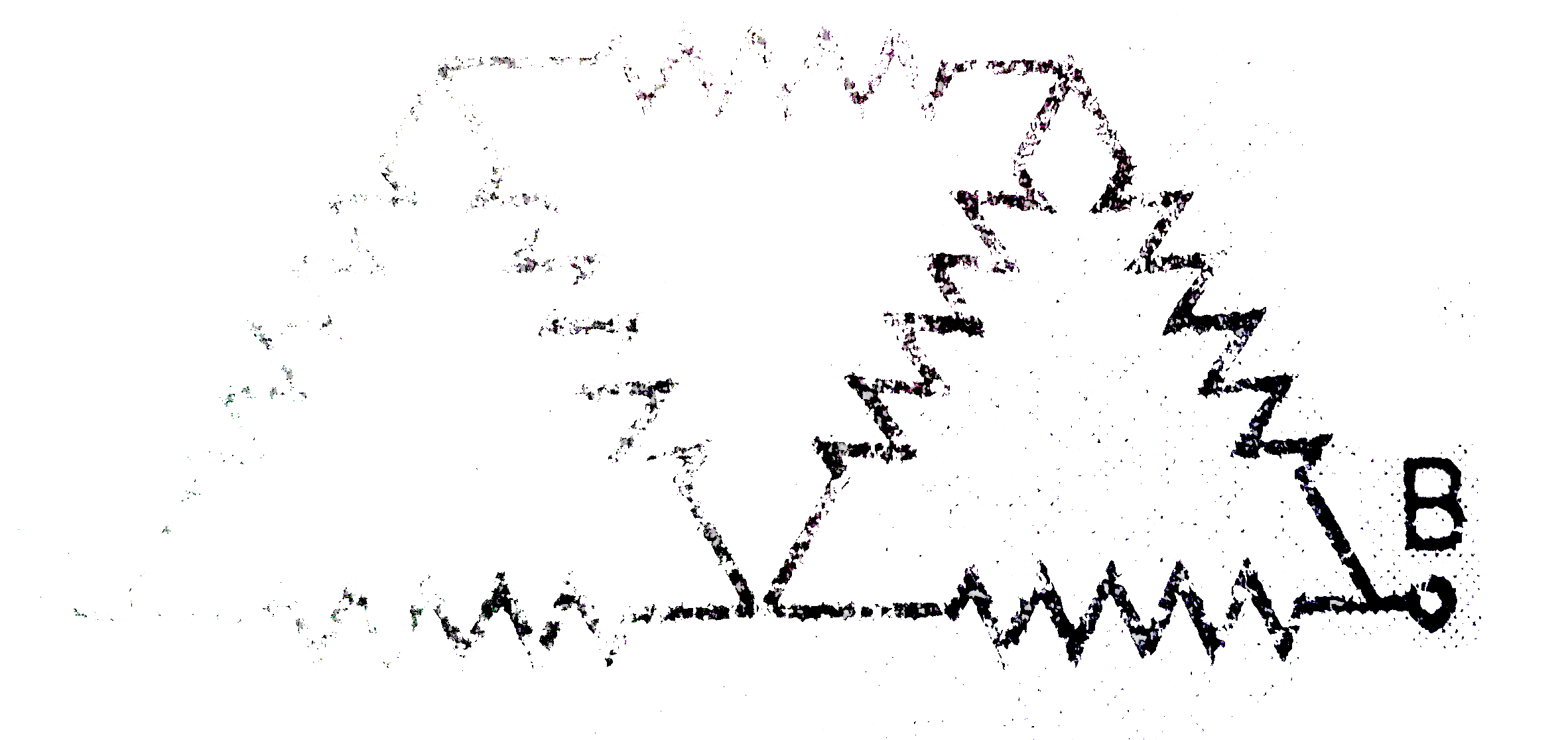
View Solution
Knowledge Check
There particles each of mass m can slide on fixed frictioless circular tracks in the same horizontal plane as shown. Particle m1(=m) moves with velocity v0 and hits particle m2(=m), the cofficient of restitution being e=0.5 . Assume that m2 and m3(=m) are at rest initially and lie along a radial line before impact, and the spring is initially unstretched.

Velocity of m2 immediately after impact isAv04B3v04Cv02D3v02Three particles each of mass 'm' can slide on fixed frictionless circular track in the same horizontal plane as shown in the figure. Particle m1 moves with velocity v0 and hits particle m2, the coefficient of restitution being θ=1/2. AsSigmae m2 and m3 are initially in rest and lie along a radial line before impact and the spring is initially Unstretched. Then,
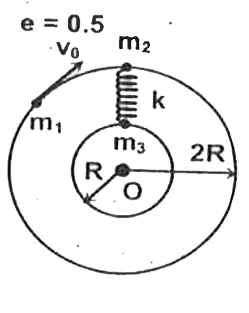
The velocity of m3 when extension in the spring is maximumA110v0B310v0C710v0Dnone of theseA skier slides horizontally along the snow for a distance of 21 m before coming to rest. The coefficient of kinetic friction between the stier and the snow is μk=0.050. Initially, how fast was the skier going ?
A6.4m/sB4.5m/sC2.7m/sD5.4m/s
A motor bike start to move on horizontal rough circular track of radius 1 m from rest with tangential acceleration 3m/s2 if coefficient of friction between road and tyre is 0.5 then at what speed in m/s bike start to slide on rough circular track.
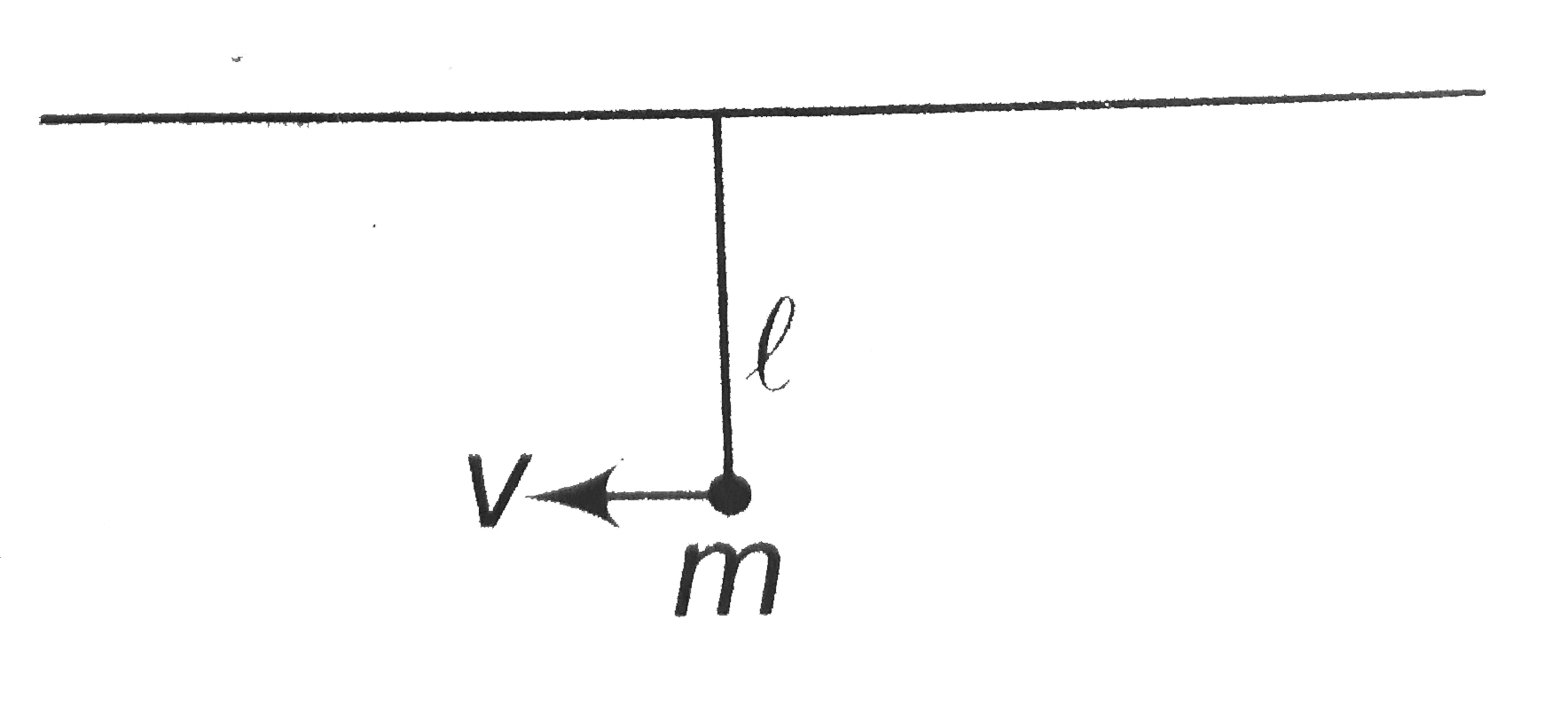
View SolutionA simple pendulum of length hangs from a horizontal roof as shown in figure. The bob of mass m is given an initial horizontal velocity of magnitude √5gl as shown in figure. The coefficient of restitution e=12. After how many collisions the bob shall no long come into constant with the horizonrtal roof?
View SolutionTwo blocks A(3kg) and B(2kg) resting on a smooth horizontal surface is connected by a spring of stiffness 480N/m. Initially the spring is underformed and a velocity of 2m/s is imparted to A along the line of the spring away from B. The maximum extension in meters of the spring during subsequent motion is :-
View Solution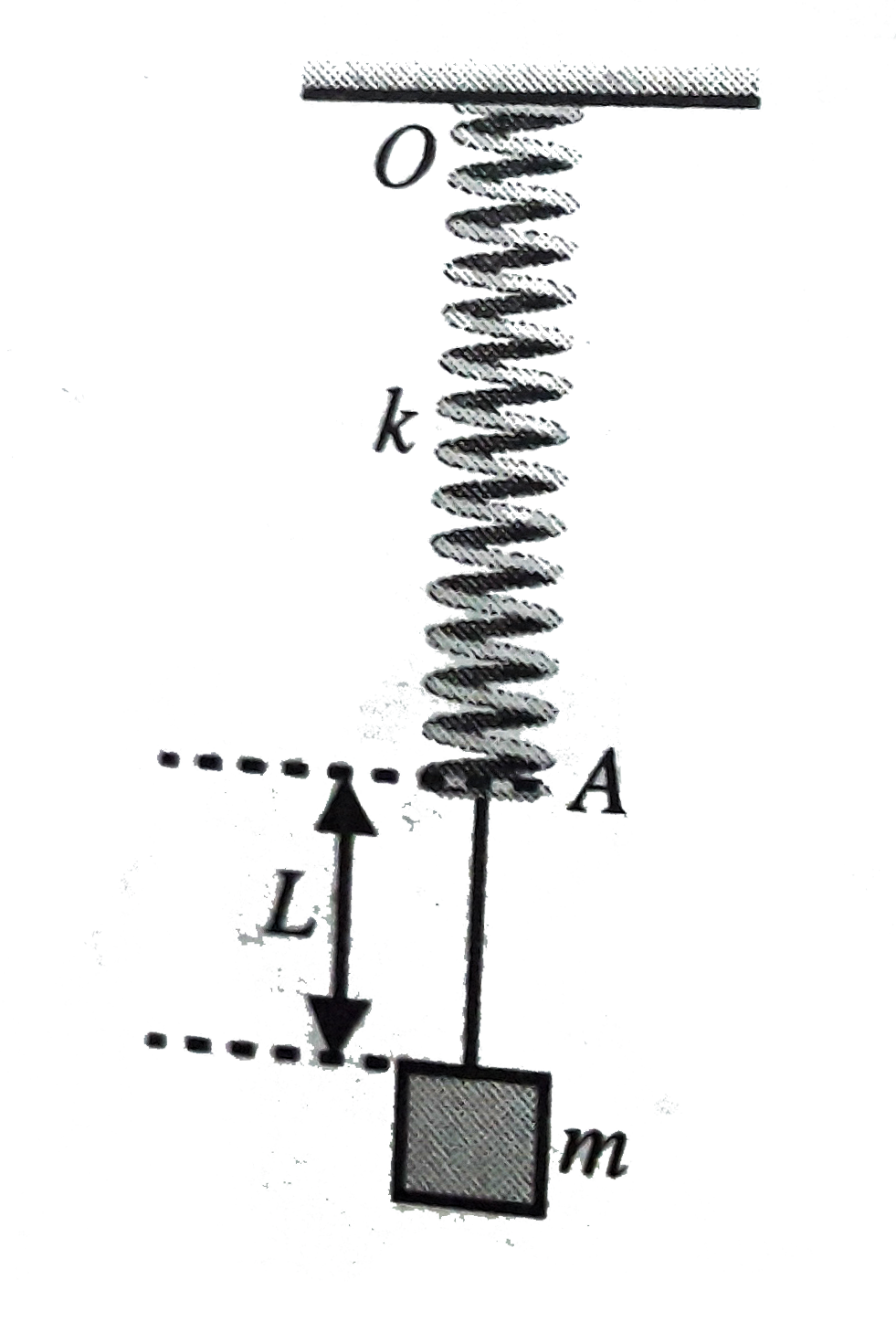
A body of mass m is attached by an inelastic string to a suspended spring of spring constant k. Both the string and the spring have negligible mass and the string is inextensible and of length L. Initially, the mass m is at rest.
Q. If the mass m is now raised up to point A (the top end of the string see fig. and allowed to fall from rest, the maximum extension of the spring in the subsequent motion will be
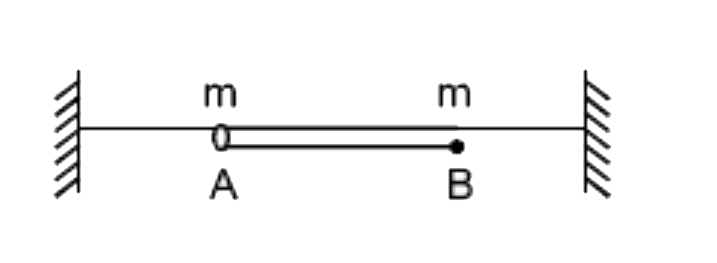
View SolutionA small ring of mass m is constrained to slide along a horizontal wire fixed between two rigid supports. The ring is connected to a particle of same mass by an ideal string & the whole system is released from rest as shown in the figure. If the coefficient of friction between ring A and wire is 35, the ring will start sliding when the connecting string will make an angle θ with the vertical, then θ will be (particle is free to move and ring can slide only)
View Solution
