A plank of mass $M$ is placed on a rough horizontal force $F$ is applied on it A man of mass m rens on the plank find the acceleration of the man so that the plank does not move on the surface . The coefficent of friction between the plank and the surface is $μ$ Assume that the man does not slip on the plank

Video Solution

Text Solution

Verified by Experts

FBD of man
$f_{1} =$ force between man and the plank
$\Rightarrow f_{1} = m a$ ….(i)
$N = m g$ …(ii)

$F B D$ of plank
Direction of friction force between ground and plank may be in forward or backward direction depending on the value of $f_{1}$ which depends on the acceleration of the man

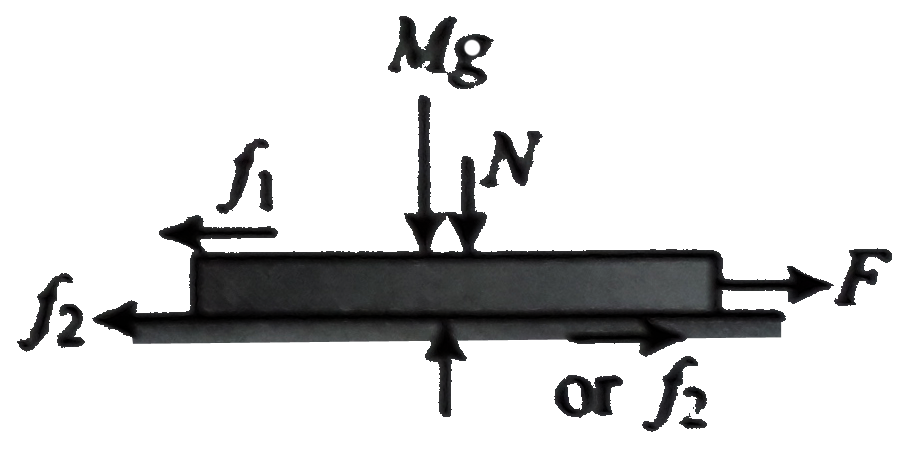
$f_{2} =$ force of friction between the plank and surface.
$f_{1}$ can have any value in the following range
$∵ F - f_{2 max} \leq f_{1} \leq F + f_{2 max}$
$\Rightarrow F - μ (m + m) g \leq m a \leq f + μ (m + M) g$
$\Rightarrow \frac{F}{m} - \frac{μ (m + M) g}{m} \leq a \leq \frac{F}{m} + \frac{μ (m + M) g}{M}$

Updated on:21/07/2023

Class 11 PHYSICS NEWTONS LAW OF MOTION

Topper's Solved these Questions

Knowledge Check

A long horizontal plank of mass $m$ is lying on a smooth horizontal surface. A sphere of same mass $m$ and radius $r$ is spinned about its own axis with angular velocity we and gently placed on the plank. The coefficient of friction between the plank and the sphere is $μ$ . After some time the pure rolling of the sphere on the plank will start. Answer the following questions.

Find the displacement of the plank till the sphere starts pure rolling.
A $\frac{ω_{0}^{2} r^{2}}{81 μ g}$
B $\frac{2 ω_{0}^{2} r^{2}}{27 μ g}$
C $\frac{4 ω_{0}^{2} r^{2}}{81 μ g}$
D $\frac{2 ω_{0}^{2} r^{2}}{81 μ g}$
A plank of mass M is placed on a rough horizontal surface. A man m walks on the plank with an acceleration 'a' while the plank is also acted upon by a horizontal force F whose magnitude and direction can be adjusted to keep the plank at rest.

The coefficient of friction between plank and surface is $μ$ . Choose the correct options.
.
AThe maximum value of F to keep plank at rest is $m a + μ (M + m) g$
BThe minimum value of F to keep the plank at rest is $m a - μ (M + m) g$
CThe direction of friction on ground due to plank will always be forward
DIf $F = m a$ then friction on man due to plank is also F and friction between plank and ground will be zero
A plank A of mass $M$ rests on a smooth horizontal surface over which it can move without friction A cabe B of mass m lies on the plank at one edge .The coefficient of friction between the plank and the cube is $μ$ The size of cube is very small in comparison to the plank.

At what force $F$ applied to the plank in the horizontal direction will be cube begin to slide towards the other end of the plank?
A $F > μ (m + M) g$
B $F > 0.5 μ (m + M) g$
C $F = 0.5 μ (m + M) g$
D $F = μ (m + M) g$

CENGAGE PHYSICS-NEWTON'S LAWS OF MOTION 2-Exercise 7.2

Home
Ask Doubt
Profile

Topper's Solved these Questions

Similar Questions

Knowledge Check

CENGAGE PHYSICS-NEWTON'S LAWS OF MOTION 2-Exercise 7.2