Two blocks of masses 3kg block is attached to a spring with a force constant, kk=900N/ma which is compressed 2m initially from its equilibrium position. When 3kg mass is released, it strikes the 6kg mass and the two stick togther in an inelastic collision.
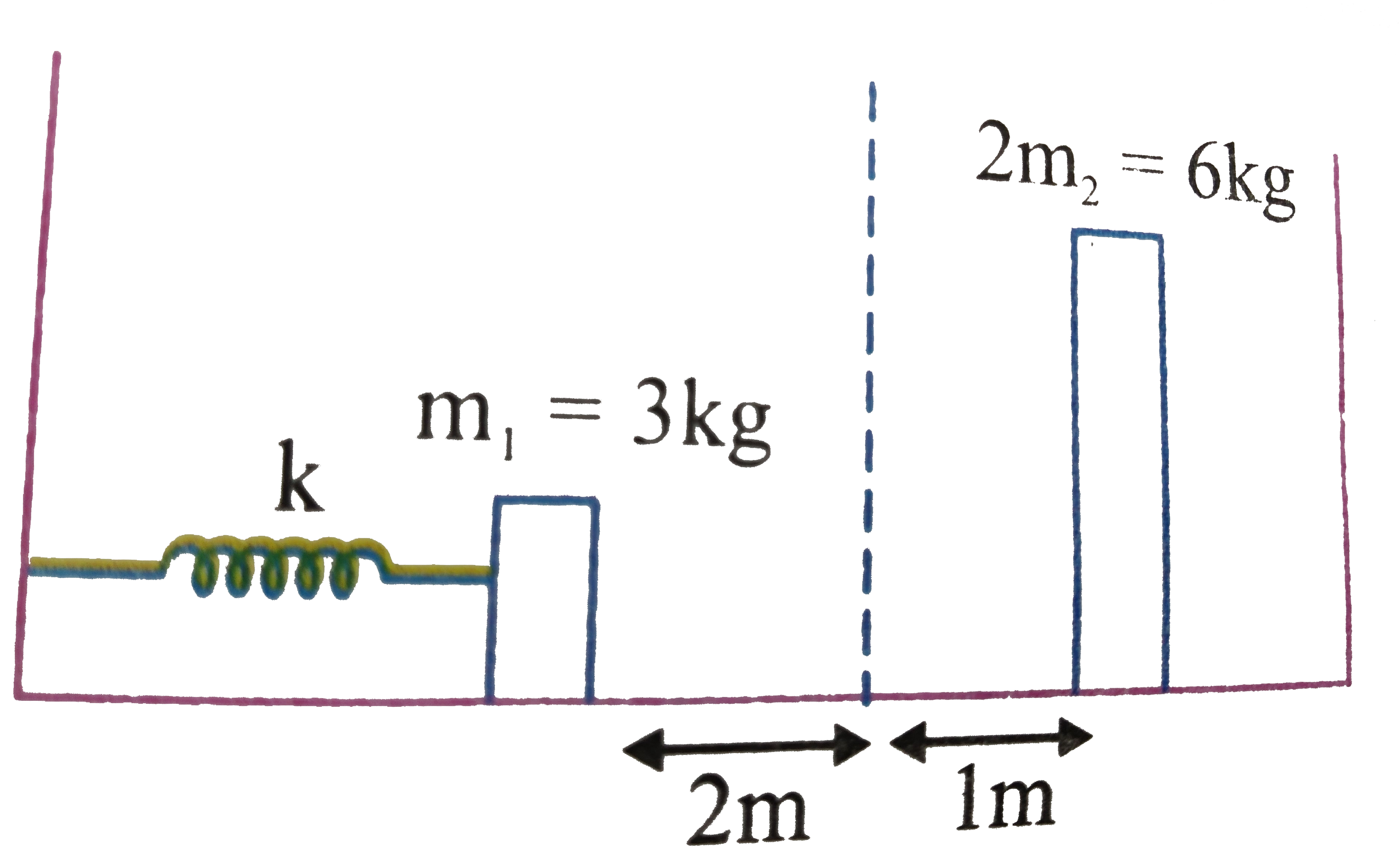
The common velocity of the blocks after collision is
10m/s
30m/s
15m/s
2m/s
The correct Answer is:A
Angular frequency of oscillation is given by ω=√km=10√3. Velocity of 3kg block at the instant it hits the 6kg block is given by v=ω√A2−x2=10√3√22−12⇒30m/s
During collision moment is conserved thus
m1v1=(m1+m2)vC⇒3×30=9×vC
or hence, common velocity of combined mass =(vC)=10m/s
Topper's Solved these Questions
- OSCILLATIONSBook:NARAYNAChapter:OSCILLATIONSExercise:Passage-VIII
Explore 1 Video
- OSCILLATIONSBook:NARAYNAChapter:OSCILLATIONSExercise:Passage-IX
Explore 1 Video
- OSCILLATIONSBook:NARAYNAChapter:OSCILLATIONSExercise:Passage-VI
Explore 1 Video
- NEWTONS LAWS OF MOTIONBook:NARAYNAChapter:NEWTONS LAWS OF MOTIONExercise:PASSAGE TYPE QUESTION
Explore 6 Videos
- PHYSICAL WORLDBook:NARAYNAChapter:PHYSICAL WORLDExercise:C.U.Q
Explore 10 Videos
Similar Questions
A block of mass m = 2 kg is attached to two unstretched spring of force constant k1=100N/m and k2=125N/m
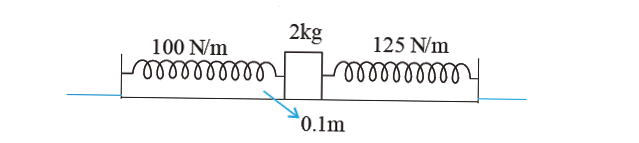
The block is displaced towards left through a distance of 10 cm and released. Find the speed of the block as it passes through the mean position.
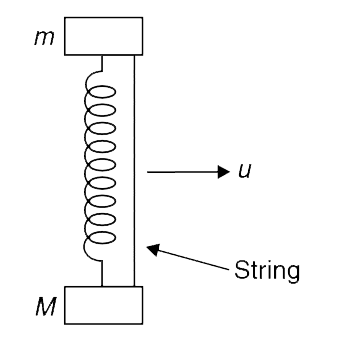
View SolutionA block A of mass 2m is hanging from a vertical massless spring of spring constant k and is in equilibrium. Another block B of mass m strikes the block A with velocity u and sticks to it as shown in the figure. The magnitude of the acceleration of the combined system of the blocks just after the collision is
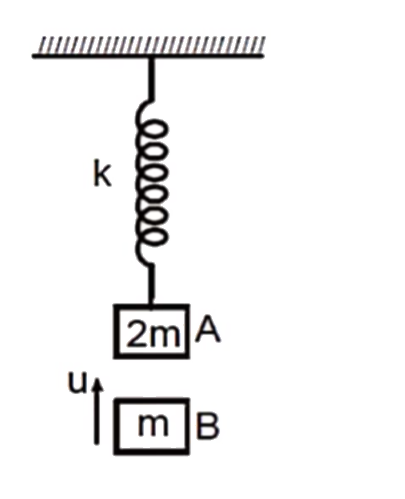
View Solution
Knowledge Check
Two blocks of masses 3kg block is attached to a spring with a force constant, kk=900N/ma which is compressed 2m initially from its equilibrium position. When 3kg mass is released, it strikes the 6kg mass and the two stick togther in an inelastic collision.
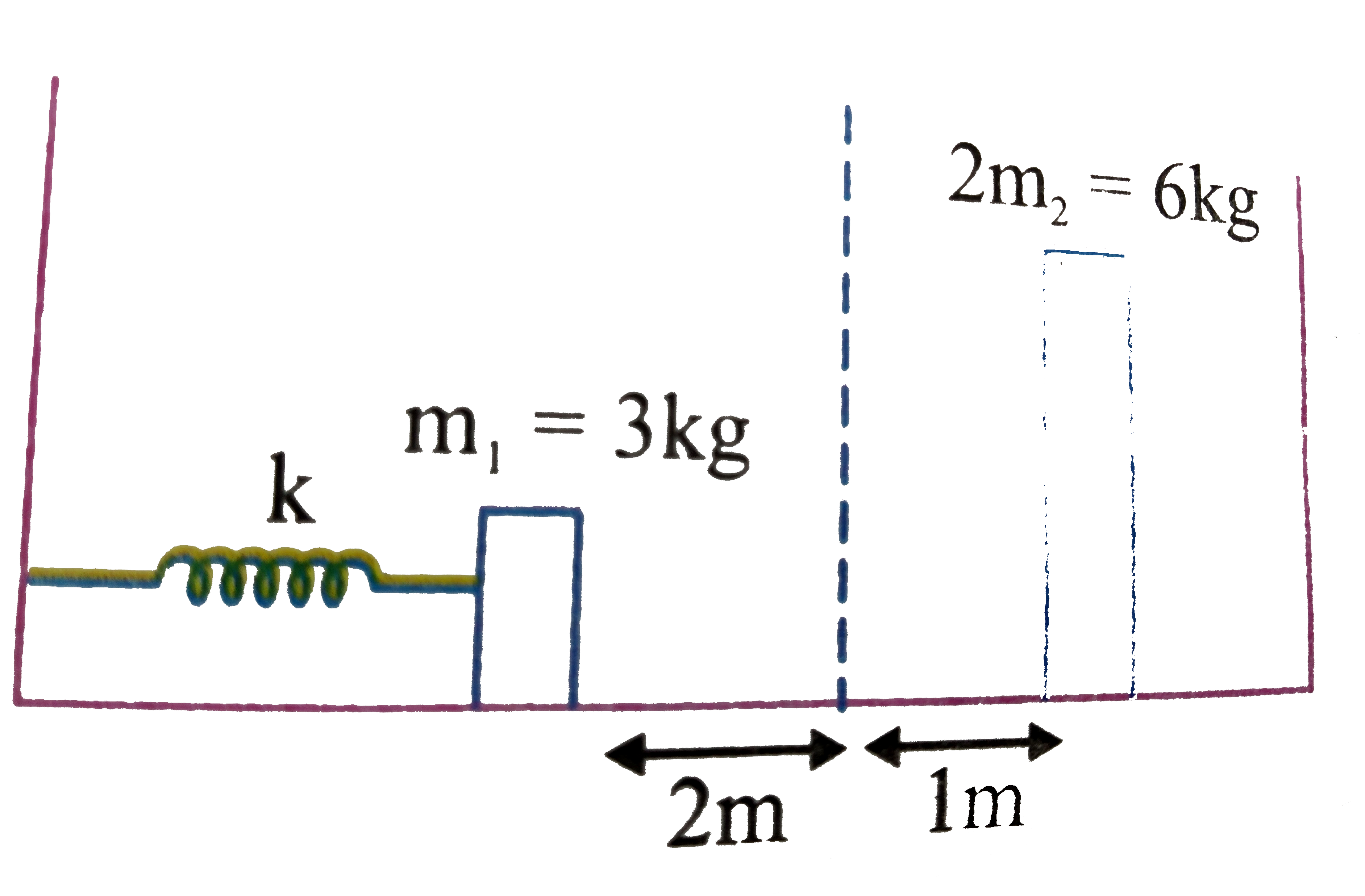
The amplitude of resulting oscillation after the collision is:A1√2mB1√3mC√2mD√3mTwo blocks of masses 3kg block is attached to a spring with a force constant, kk=900N/ma which is compressed 2m initially from its equilibrium position. When 3kg mass is released, it strikes the 6kg mass and the two stick togther in an inelastic collision.
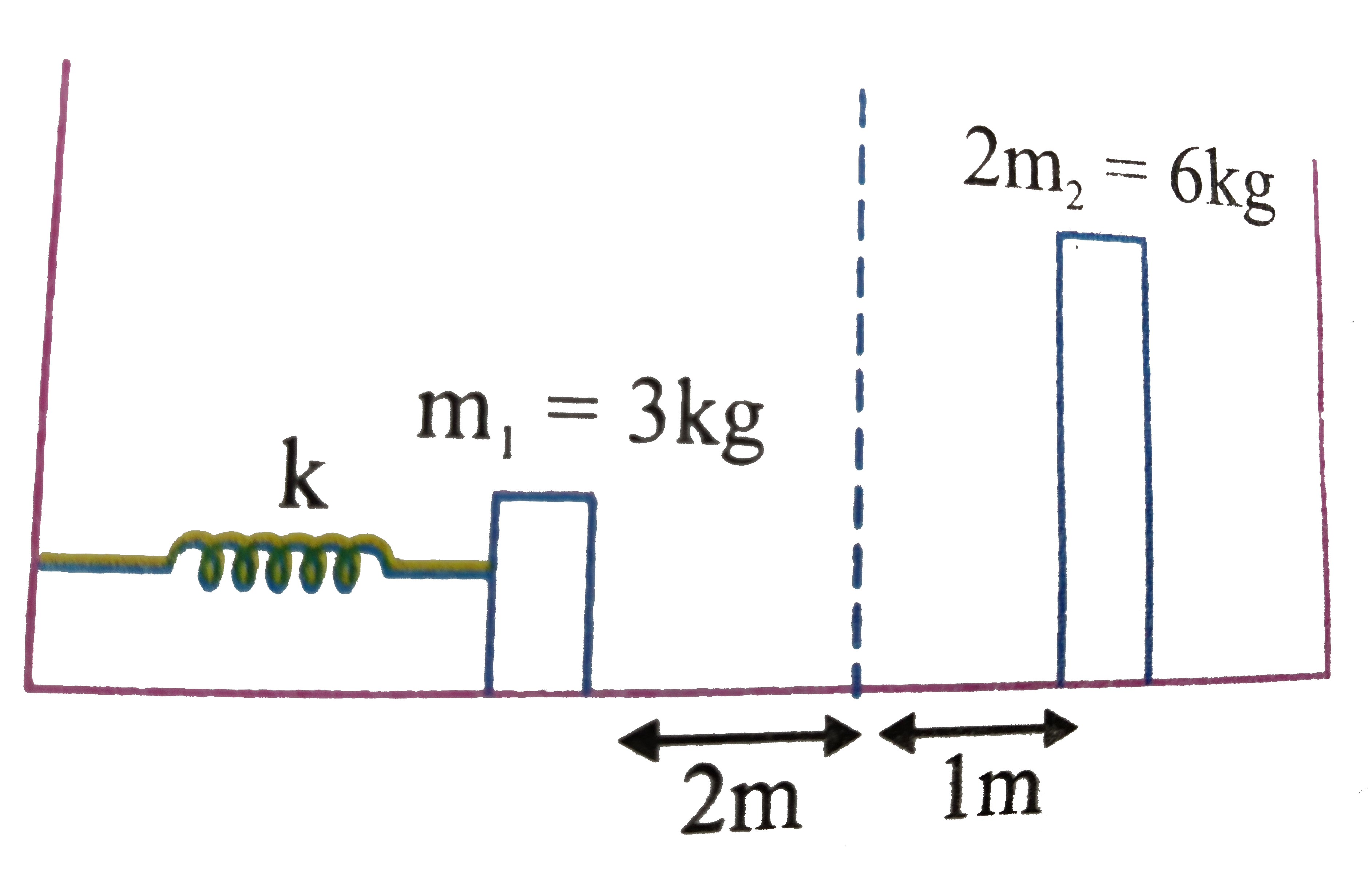
The velocities of a particle executing S.H.M. are 30cm/s and 16cm/s when its displacements are 8cm and 15cm from the equilibrium position. then its amplitude of oscillation in cm is:A25B21C17D13Two blocks of masses 3kg and 6kg rest on a horizontal smooth surface. The 3kg block is attached to a spring with a force constant k=900Nm−1 which is compressed 2m from beyond the equilibrium position. 3kg mass strikes the 6kgmass and two stick together-
 Avelocity of the combined masses immediately arter the collision is 10ms−1Bvelocity of the conbined masses immediately after the collision is 5ms−1CAmplitude of the resulting oscillation is √2mDAmplitude of the resulting oscillation is √5/2m
Avelocity of the combined masses immediately arter the collision is 10ms−1Bvelocity of the conbined masses immediately after the collision is 5ms−1CAmplitude of the resulting oscillation is √2mDAmplitude of the resulting oscillation is √5/2m
Two blocks of masses m=2kgandm=8kg are connected to a spring of force constant K=1kN/m. The spring is compressed by 20cm and the two blocks are held in this position by a string. The system is placed on a horizontal smooth surface and given a velocity u=3m/s perpendicular to the spring. The string snaps while moving. Find the speed of the block of mass m when the spring regains its natural length.
View SolutionTwo blocks of masses 3 kg and 6kg rest on horizontal smooth surface. The 3 kg block is attached to a spring with a long constant k=900Nm−1 which is compressed 2m from beyond 1m from mean position. 3kg mass strikes the 6 kg mass and the two stick together.

View SolutionA block of mass m length force a verical of spring constant k If the block is polled down by a distance of 2mg/k from its equilibrium position and released for the subsequent in the spring to maximum compressed in it mg/k
View SolutionA block of mass m=0.1kg is connceted to a spring of unknown spring constant k. It is compressed to a distance x from its equilibrium position and released from rest. After approaching half the distance (x2) from the euilibrium position, it hits another block and comes to rest momentarily, while the other block moves with velocity 3ms−1. The total initial energy of the spring is :
View SolutionTwo block A and B of masses m and 2m respectively are connected by a spring of spring cosntant k. The masses are moving to the right with a uniform velocity v0 each, the heavier mass leading the lighter one. The spring is of natural length during this motion. Block B collides head on with a thrid block C of mass 2m. at rest, the collision being completely inelastic.

The velocity of block B just after collision is -
View Solution

