A block of mass m length force a verical of spring constant k If the block is polled down by a distance of 2mg/k from its equilibrium position and released for the subsequent in the spring to maximum compressed in it mg/k
2
3
4
1
The correct Answer is:A
Maximum extension: x=4mg/k
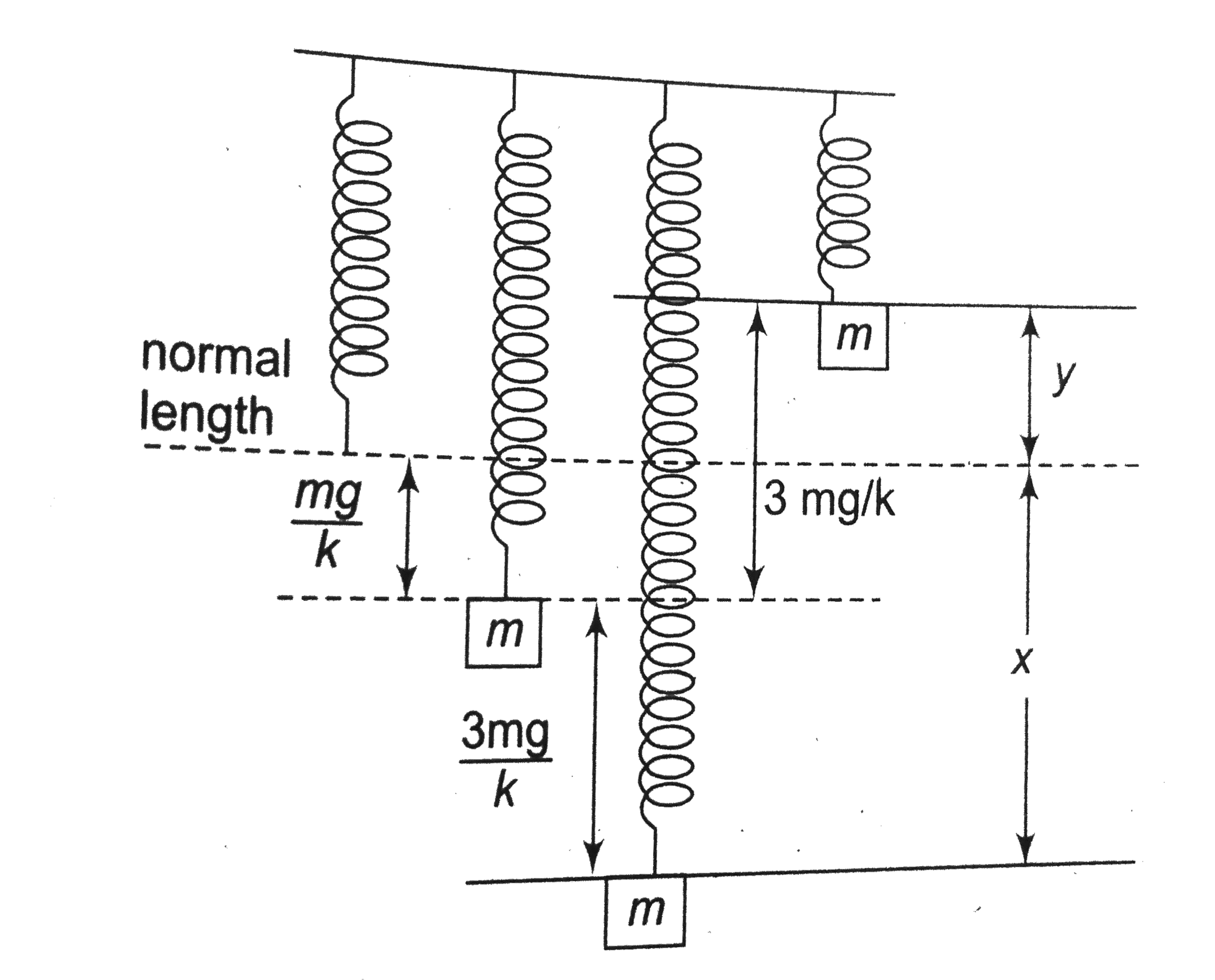
Maximum compression: y=2mg/k
Topper's Solved these Questions
- OSCILLATION AND SIMPLE HARMONIC MOTIONBook:A2ZChapter:OSCILLATION AND SIMPLE HARMONIC MOTIONExercise:Simple Pendulum And Different Cases Of Shm
Explore 25 Videos
- OSCILLATION AND SIMPLE HARMONIC MOTIONBook:A2ZChapter:OSCILLATION AND SIMPLE HARMONIC MOTIONExercise:Superposition Of Shm And Compound Pendulum
Explore 19 Videos
- OSCILLATION AND SIMPLE HARMONIC MOTIONBook:A2ZChapter:OSCILLATION AND SIMPLE HARMONIC MOTIONExercise:Velocity , Acceleration And Energy Of Simple Harmonic Motion
Explore 40 Videos
- NEWTONS LAWS OF MOTIONBook:A2ZChapter:NEWTONS LAWS OF MOTIONExercise:Chapter Test
Explore 30 Videos
- PROPERTIES OF MATTERBook:A2ZChapter:PROPERTIES OF MATTERExercise:Chapter Test
Explore 29 Videos
Similar Questions
Knowledge Check
An elastic string of constant k is attached to a block of mass m as shown. The block is given an extension of 2mgk from the equilibrium position and released. The time period of oscillations of the block is
 A2π√mkB4√mk(π3+√3)C2π√mk+2√3√mkDπ√mk+√3√mk
A2π√mkB4√mk(π3+√3)C2π√mk+2√3√mkDπ√mk+√3√mkA block is suspended by an ideal spring of force constant k. If the block is pulled down by applying a constant force F and if maximum displacement of the block from its initial position of rest is δ, then
A(a) Fk<δ>2FkB(b) δ=2FkC(c) Work done by force F is equal to FδD(d) Increase in energy stored in the spring is 12kδ2Figure shows a system consisting of a massless pulley, a spring of force constant k and a block of mass m. If the block is slightly displaced vertically down from is equilibrium position and then released, the period of its vertical oscillation is
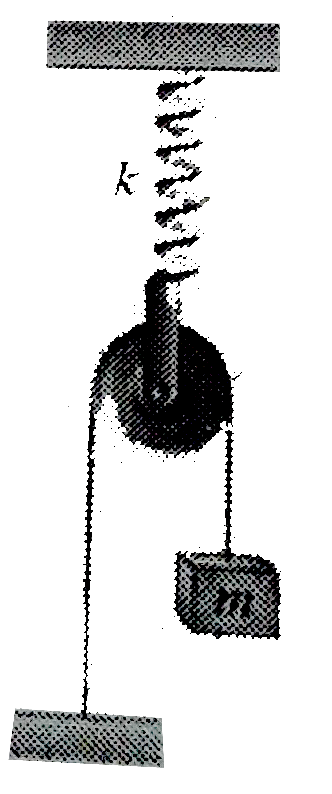 A2π√mKBπ√m4KCπ√mKD4π√mK
A2π√mKBπ√m4KCπ√mKD4π√mK
A block whose mass m is 680g is fastened to a spring whose spring constant k is 65N/m. The block is pulled a distance x=11cm from its equilibrium position at x=0 on a frictionless surface and released from rest at t= 0.
What is the phase constant ϕ for the motion?
View SolutionA block whose mass m is 680g is fastened to a spring whose spring constant k is 65N/m. The block is pulled a distance x=11cm from its equilibrium position at x=0 on a frictionless surface and released from rest at t= 0.
What is the amplitude of the oscillation?
View SolutionA block of mass m moving at a speed v0 compresses a spring of spring constant k as shown in the figure. Find (a) the maximum compression of spring and (b) speed of the block when the spring is compressed to half of maximum compression.
View Solution
A block of mass m is pushed against a spring of spring constant k fixed at one end to a wall.The block can slide on a frictionless table as shown in the figure. The natural length of the spring is L0 and it is compressed to one fourth of natural length and the block is released.Find its velocity as a function of its distance (x) from the wall and maximum velocity of the block. The block is not attached to the spring.
View SolutionA block of mass m is attached to two unstretched springs of spring constant k1 and k2 as shown in figure. The block is displaced towards right through a distance 'x' and is released. Find the speed of the block as it passes through a distance x/4 from its mean position. All the surfaces are smooth.
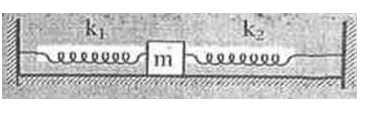
View Solution

