Two light spring of force constants k1andk2 and a block of mass m are in the line AB on a smooth horizontal table such that one end of each spring is fixed on right supports and the other and is free as shown in figure

The distance CD between the free ends of the spring is 60cm. If the block moves with a velocity of 120cm/s between C and D and (k1=1.8N/m,k2=3.2N/mandm=200g). Is the motion simple harmonic?
1.04sec
0.785sec
1sec
2.82sec
The correct Answer is:D
t=t1+t2+t3, let C',D' be the exterme positions of the springs k2,k1 respectively.
t1=tDL+tD'D=T12=π√mk1
∴T2=tDC+tCD=2Lv,t3=tCC'+tC'C=T22=π√mk2
Topper's Solved these Questions
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - Passage-VI
1 Videos
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - Passage-VII
1 Videos
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - Passage-V
2 Videos
- NEWTONS LAWS OF MOTIONBOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - PASSAGE TYPE QUESTION
6 Videos
- PHYSICAL WORLDBOOK - NARAYNACHAPTER - PHYSICAL WORLDEXERCISE - C.U.Q
10 Videos
Similar Questions
Two light spring of force constants k1andk2 and a block of mass m are in the line AB on a smooth horizontal table such that one end of each spring is fixed on right supports and the other and is free as shown in figure

The distance CD between the free ends of the spring is 60cm. If the block (k1=1.8N/m,k2=3.2N/mandm=200g). Is the motion simple harmonic?
View SolutionTwo light springs of force constants (k_1 and k_2) and a block of mass (m) are in one line (AB) on a smooth horizontal table such that one end of each spring is fixed on rigid supports and the other end is free as shown in the figure. The distance (CD) between the free ends of the springs is (60 cms). If the block moves along (AB) with a velocity (120 cm//sec) in between the springs, calculate the period of oscillation of the block k1=1.8N/m,k2=3.2N/m,m=200gm).
(##JMA_CHMO_C10_026_Q01##).
View Solution
Knowledge Check
A block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. Two maximum compression in spring is
 A√2mkv0B√mk.v0C√mk.v0Dm2k.v0
A√2mkv0B√mk.v0C√mk.v0Dm2k.v0A block of mass m, attacted to a string of spring constant k, oscillates on a smooth horizontal table. The other end of the spring is fixed to a wall. The block has a speed v when the spring is at its natural length. Before coming to an instantaneous rest. If the block moves a distance x from the mean position, then
Ax=√mkBa=1v√mkCx=v√mkDx=√mvkAs shown in the figure, two light springs of force constant k1 and k2 oscillate a block of mass m. Its effective force constant will be
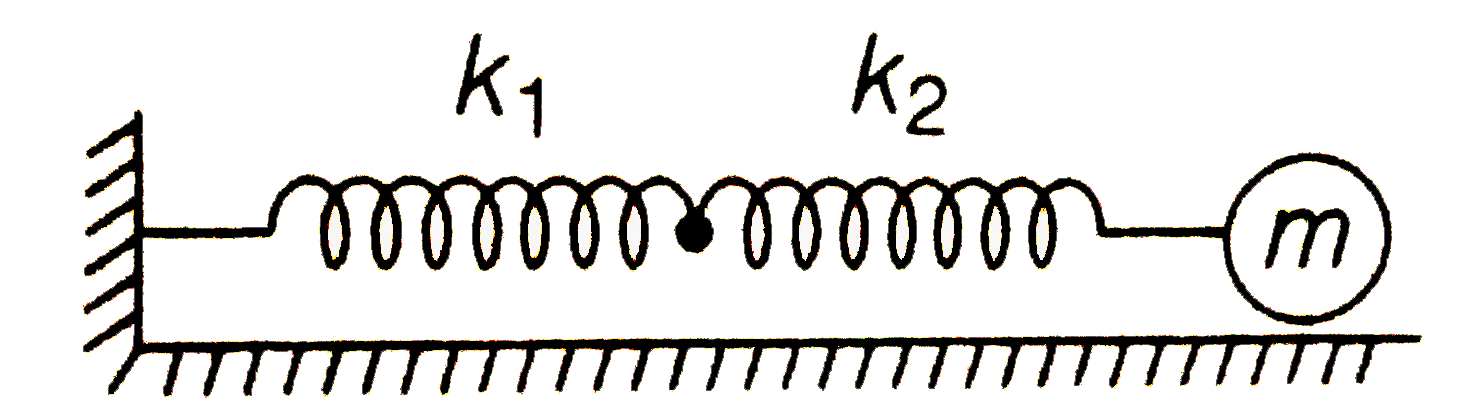 Ak1k2Bk1+k2C1k1+1k2Dk1k2k1+k2
Ak1k2Bk1+k2C1k1+1k2Dk1k2k1+k2
Two identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in the figure. The time period of oscillation is

View SolutionA block of mass m, lying on a smooth horizontal surface, is attached to a spring (of negligible mass) of spring constant k. The other end of the spring is fixed, as shown in the figure. The block is initally at rest in its equilibrium position. If now the block is pulled withe a constant force F, the maximum speed of the block is :

View SolutionA block of mass m, lying on a smooth horizontal surface, is attached to a spring (of negligible mass) of spring constant k. The other end of the spring is fixed, as shown in the figure. The block is initally at rest in its equilibrium position. If now the block is pulled withe a constant force F, the maximum speed of the block is :

View SolutionA block of mass m sliding n a smooth horizontal surface with velocity →v meets a long horizontal spring fixed ast one end and having spring constant k as shown n figure. Find the maximum compression of the spring. Will the velocity of the block be the same as v whenit comes back to the original position shown?

View SolutionA block of mass m compresses a spring iof stifffness k through a distacne l/2 as shown in the figure .If the block is not fixed to the spring the period of motion of the block is
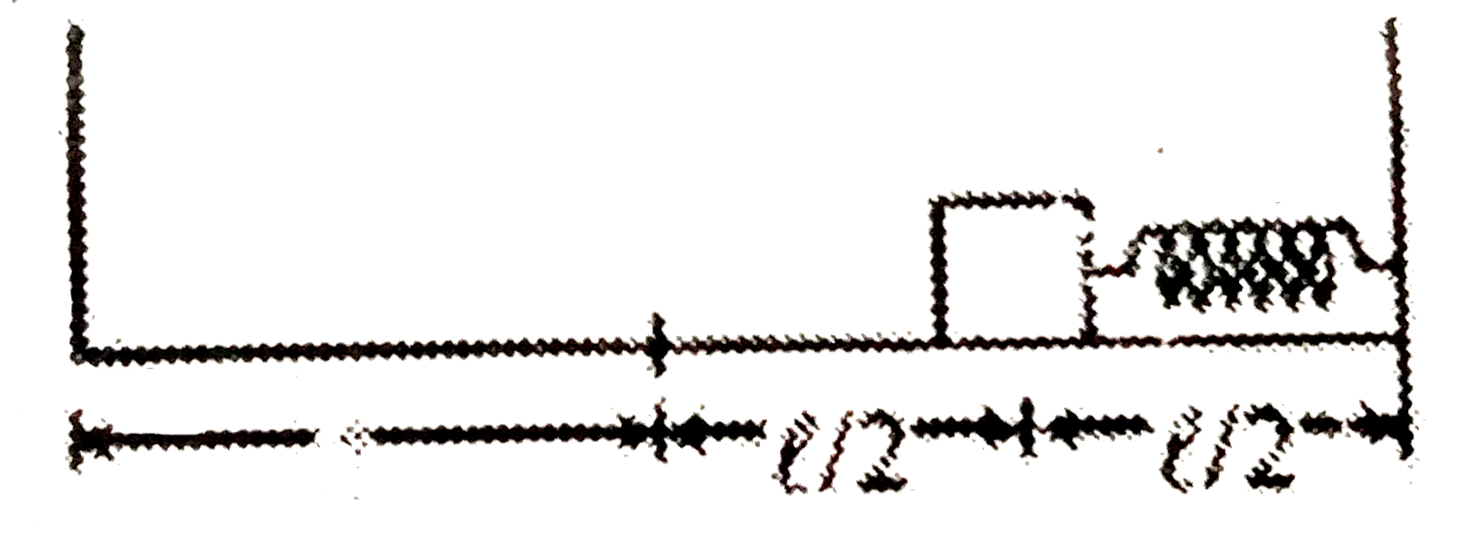
View Solution
