Two identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in the figure. The time period of oscillation is

2π√mk
2π√mk
2π√2mk
π√m2k
The correct Answer is:B
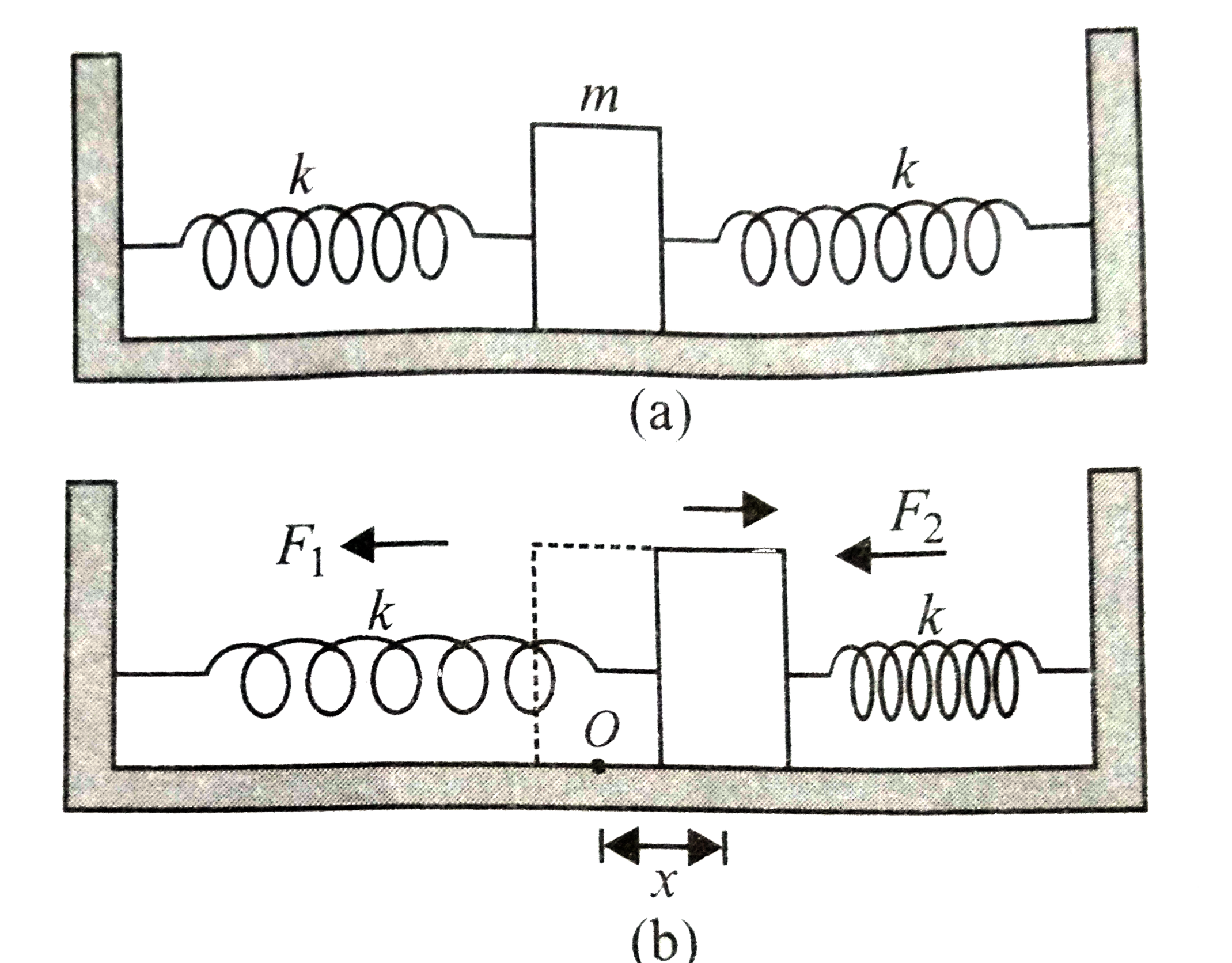
Let the mass m be displaced by a small distance x to the right from its mean position as shown in figure (b). Due to it’s the spring on the left side gets stretched by a length x while that on the right side gets compressed by the sae length. the forces acting on the mass are the same length. the forces acting on the mass are
F1=−kx towards left hand side
F2=−kx towards left hand side
The net force acting on the mass is, F=F1=−2kx
Here, F∝xand−ve sign shows that force is towards the mean position, therefore the motion executed by the particle is simple harmonic.
Its acceleration is
a=Fm=−2kxm . . . (i)
the standard equation of SHM is
a=−ω2x . . . (ii)
Comparing (i) and (ii), we get
ω2=2km or ω=√2km
time period, T=2πω=2π√m2k
Topper's Solved these Questions
- OSCILLATIONS Book:NCERT FINGERTIPSChapter:OSCILLATIONS Exercise:Damped Simple Harmonic Motion
Explore 5 Videos
- OSCILLATIONS Book:NCERT FINGERTIPSChapter:OSCILLATIONS Exercise:Forced Oscillation And Resonance
Explore 6 Videos
- OSCILLATIONS Book:NCERT FINGERTIPSChapter:OSCILLATIONS Exercise:Energy In Simple Harmonic Motion
Explore 11 Videos
- MOTION IN A STRAIGHT LINEBook:NCERT FINGERTIPSChapter:MOTION IN A STRAIGHT LINEExercise:Assertion And Reason
Explore 15 Videos
- PHYSICAL WORLDBook:NCERT FINGERTIPSChapter:PHYSICAL WORLDExercise:Assertion And Reason
Explore 10 Videos
Similar Questions
Two identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in figure. When the mass is displaced from equilibrium position by a distance x towards right, find the restoring force.

View SolutionTow identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in figure. When the mass is displaced from equilibrum position by a distance x towards right, find the restoring force.

View Solution
Knowledge Check
A block of mass m is connected to two indentical springs of spring constant k which are in turn connected to fixed supports as shown in the figure. Find the time period for small oscillations of the block.
 A2π√mkB2π√m2kC2π√2mkDπ√m2k
A2π√mkB2π√m2kC2π√2mkDπ√m2kTwo springs of spring constant 6N/m and 4N/m are attached to a block of mass 1 kg and to fixed support. Then time period of the given oscillation is
(consider √10=π)A1sB2sC0.5sD4sA tray of mass M = 10 kg executes SHM of period 1.5s. It is supported on two identical springs of spring constant k as shown in figure. If a block of mass m is also placed on the tray, the period of oscillation increases to 3s. The value of m is:
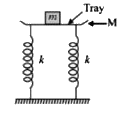 A10 kgB20 kgC30 kgD40 kg
A10 kgB20 kgC30 kgD40 kg
Two identical springs of spring constant k are attached to a block of mass m and to fixed supports as shwon in figure . Show that when the mass is displaced from its equilibrium position on either side, it executes a simple harmonic motion. Find th eperiod of oscillation.

View SolutionTwo identical springs of spring constant '2k' are attached to a block of mass m and to fixed support (see figure).When the mass is displaced from equilibrium position on either side, it executes simple harmonic motion. The time period of oscillations of this sytem is :

View SolutionTwo springs, each of spring constant k, are attached to a block of mass m as shown in the figure. The block can slide smoothly alongs a horizontal platform clamped to the oppsite walls of the trolley of mass M. If the block is displaced by xcm and released, the period of oscillaion is :

View SolutionA mass m is suspended from a spring of force constant k and just touches another idential spring fixed to the floras shown in the figure. The time period of small oscillation is

View Solution
A mass m is suspended from a spring of force constant k and just touches another identical spring fixed to the floor as shown in the fig. The time period of small oscillations is
View Solution