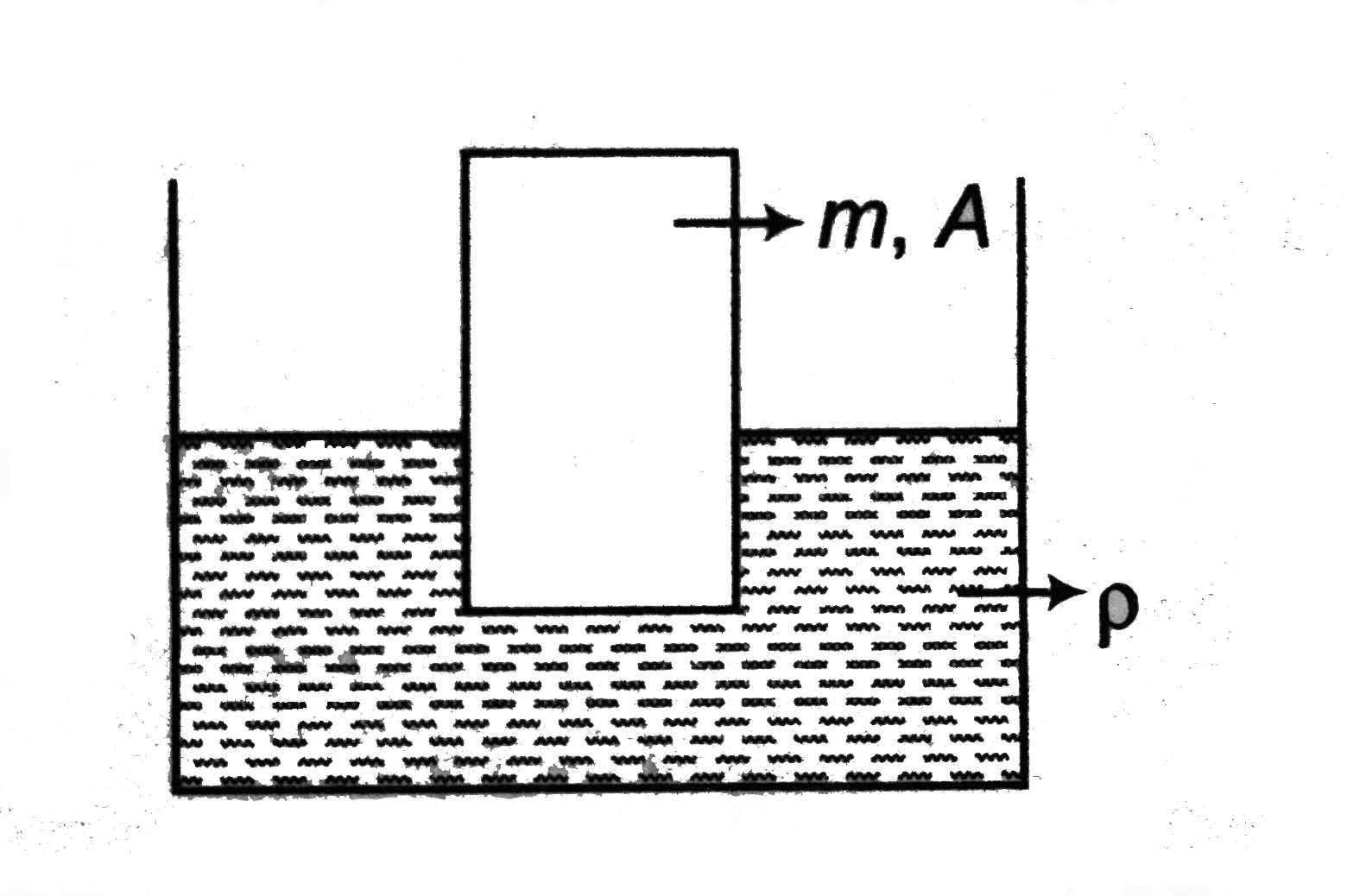
A rectangular block of mass m and area of cross-section A floats in a liquid of density ρ. If it is given a small vertical displacement from equilibrium, it undergoes oscillation with a time period T. Then

A

T∝1√m

B

T∝√ρ

C

T∝1√A

D

T∝1ρ

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:C

ocr_image
Refer figure, Let h to be the height of block immersed in liquid, when the block si floating.
∴mg=Ahρg . . . (i)
If the block is given a vertical displacement y, then the effective restoring force is
F=−[A(h+y)ρg−mg]=−[A(h+y)ρg−Ahρg]
=−Aρgy . . . (ii)
i.e., F∝yand−ve sign shown that F is directed towards its equilibrium position of block. so, if the block is left free, it will execute SHM
for SHM, F=−mω2y . . . (iii)
Comparing (ii) and (iii), we get
Aρg=mω2,ω=√Aρgm
∴Time period, T=2πω=2π√mAρg⇒T∝1√A.

Updated on:21/07/2023
|
Class 11PHYSICSSIMPLE HARMONIC MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • A rectangular block of mass m and area of cross-section A floats in a liquid of density ρ. If it is given a small vertical displacement from equilibrium, it undergoes oscillation with a time period T.
    (i) T∝√m
    (ii) T∝√ρ
    (iii) T∝1√A
    (iv) T∝1√ρ.

    A(i),(ii),(iii)
    B(i),(iii),(iv)
    C(i),(iii)
    D(iii),(iv)

  • A rectangular block of mass m and area of cross-section A floats in a liquid of density ρ. If it is given a small vertical displacement from equilibrium, it undergoes oscillation with a time period T. Then

    AT∝√ρ
    BT∝1√A
    CT∝1√ρ
    DT∝1√m

  • A rectangular block of mass m and area of cross-section A floats in a liquid of density ρ. If it is given a small vertical displacement from equilibrium, it undergoes oscillation with a time period T. Then

    AT∝√ρ
    BT∝1√A
    CT∝1∝
    DT∝1√m