The time period of small oscillations of mass m :-
_S01_040_Q01.png)
2π√m6k
2π√11m6K
2π√6m11K
2π√mK
The correct Answer is:B
Equivalent spring constant 1Keq=13K+12K+1K⇒Keq=6K11∴T2π√mKeq=2π√11m6K
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise-01
117 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise-02
19 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
25 Videos
- TEST PAPERBOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
Similar Questions
A light pulley is suspended at the lower end of a spring of constant k1, as shown in figure. An inextensible string passes over the pulley. At one end of string a mass m is suspended, the other end of the string is attached to another spring of constant k2. The other ends of both the springs are attached to rigid supports, as shown. Neglecting masses of springs and any friction, find the time period of small oscillations of mass m about equilibrium position.

View SolutionThree spring mass systems in vertical plane are shown in the figure. The mass of all the pulleys and connecting strings and springs are negligible and friction at all contacts is absent. [g=10m/s2]
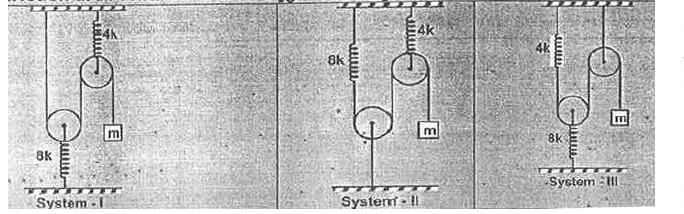
Calculate T1,T2andT3 which are the time periods of small vertical oscillation of mass m in system, l system - II and system -III respectively.
View Solution
Knowledge Check
The potential energy of a peticle of mass 'm' situated in a unidimensional potential field varies as U(x)=0[1−cosax], where U0 and a are constants. The time period of small oscillations of the particle about the mean positions is :
A2π√maU0B2π√amU0C2π√ma2U0D2π√32mU0The potential energy of a peticle of mass 'm' situated in a unidimensional potential field varies as U(x)=0[1−cosax], where U0 and a are constants. The time period of small oscillations of the particle about the mean positions is :
A2π√maU0B2π√amU0C2π√ma2U0D2π√32mU0The time period of an oscillating spring of mass 630 g and spring constant 100 N/m with a load of 1 kg is
A0.2πsB0.21πsC0.22πsD0.02πs
A mass m is suspended from a weightless spring. The time period of oscillation of mass is 3 s . Calculate the value of m if on suspending an additional mass of 3kg, time period increases by 2 s.
View SolutionA square plate of mass M and side length L is hinged at one of its vertex (A) and is free to rotate about it. Find the time period of small oscillations if
(a) the plate performs oscillations in the vertical plane of the figure. (Axis is perpendicular to figure.)
(b) the plate performs oscillations about a horizontal axis passing through A lying in the plane of the figure.

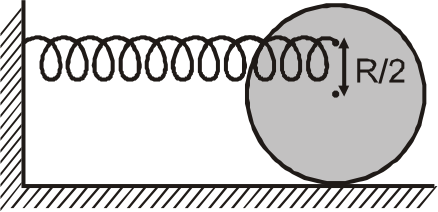
View SolutionA uniform disc of mass m is attached to a spring of spring constant k as shown in figure and there is sufficient friction to prevent slipping of disc. Time period of small oscillations of disc is:
View SolutionThe ratio of the time periods of small oscillation of the insulated spring and mass system before and after charging the masses is
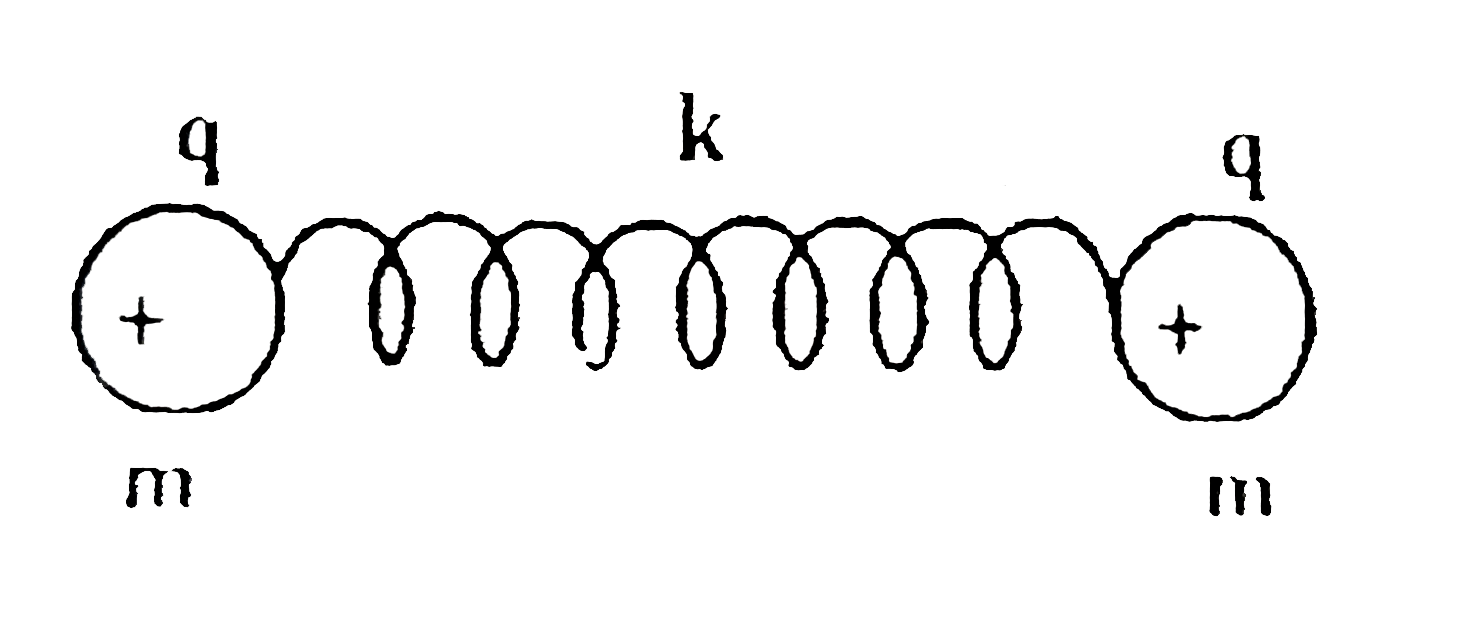
View SolutionA system is shown in the figure. The force The time period for small oscilations of the two blocks will be

View Solution
