A light pulley is suspended at the lower end of a spring of constant k1, as shown in figure. An inextensible string passes over the pulley. At one end of string a mass m is suspended, the other end of the string is attached to another spring of constant k2. The other ends of both the springs are attached to rigid supports, as shown. Neglecting masses of springs and any friction, find the time period of small oscillations of mass m about equilibrium position.

The correct Answer is:A, B, D
Let F be the extra tension in the string, when the block is displaced x from its mean position.
Extention in spring −2 is
x2=Fk2
Extension is spring −1 is
x1=2Fk1
x=2x1+x2=4Fk1+Fk2
Extra tension F will become restoring force for the block. Therefore, above equation can be written as,
F=−⎛⎜⎝14k1+1k2⎞⎟⎠x=(k1k24k2+k1)x
or ke=k1k24k2+k1
T=2π√mke
=2π√m(4k2+k1)k1k2
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise 14.1
5 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Intro. Exer.
1 Video
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 2 Comprehension
2 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEY ENGLISHCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)
38 Videos
Similar Questions
A ring of mass m and radius a is connected to an inextensible string which passes over a frictionless pulley. The other end of string is connected to upper end of a massless spring of spring constant k. The lower end of the spring is fixed. The ring can rotate in the vertical plane about hinge without any friction. If horizontal position of ring is equilibrium position then find time period of small in oscillations of the ring.
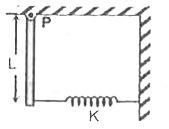
View SolutionA straight rod of light L and mass m is pivoted freely from a point of the roof. Its lower end is connected to an ideal spring of spring constant K. The other end of the spring is connected to the wall as shown in the figure. Find the frequency of small oscillation of the system.
View Solution
Knowledge Check
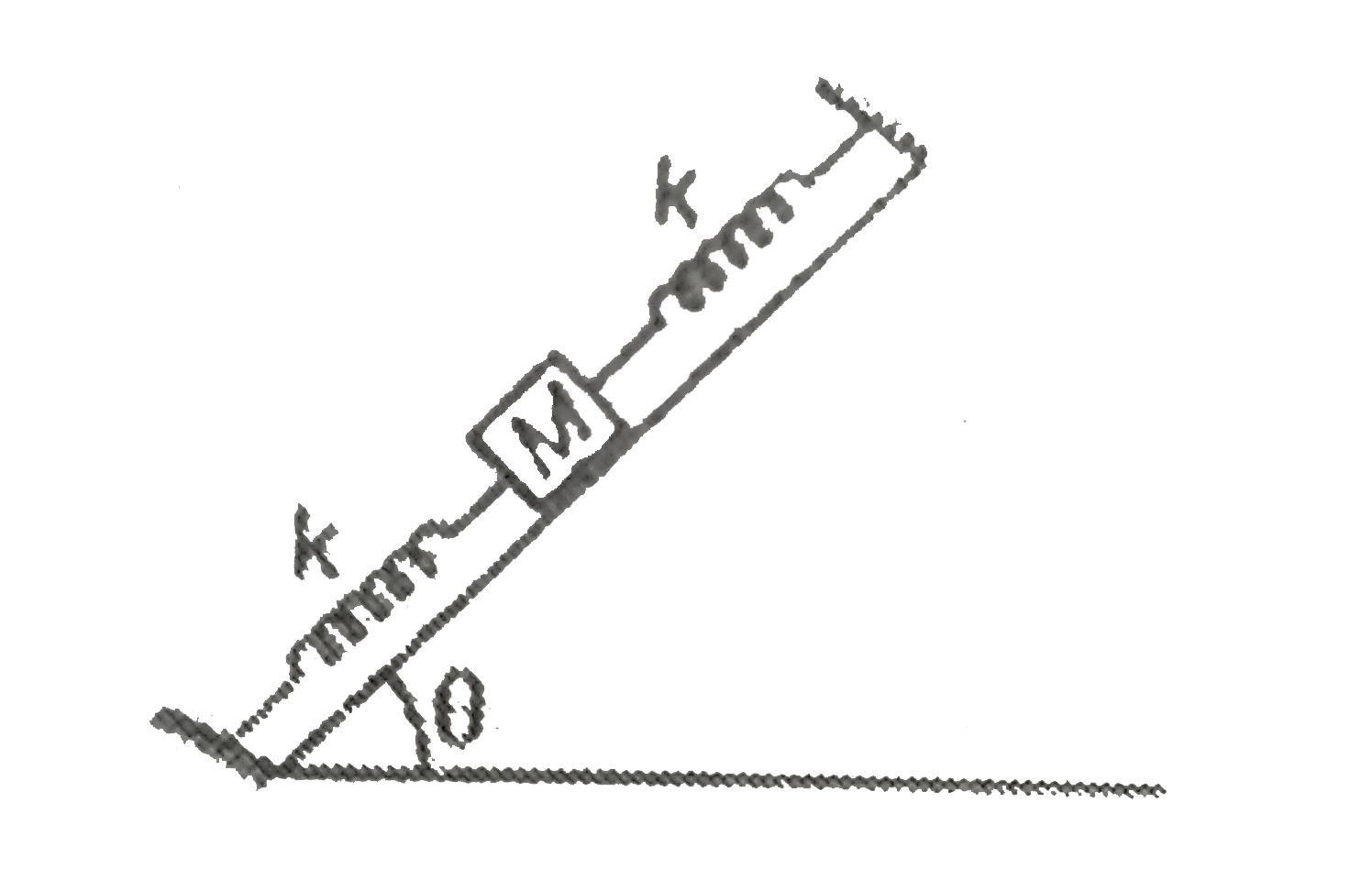
On a smooth inclined plane, a body of mass M is attached between two springs. The other ends of the springs are fixed to firm supports. If each spring has force constant K , the period of oscillation of the body (assuming the springs as massless) is
 A1. 2π√M2kB2. 2π√2MkC3. 2π√Mgsinθ2kD4. 2π√2Mgk
A1. 2π√M2kB2. 2π√2MkC3. 2π√Mgsinθ2kD4. 2π√2Mgk
A mass of 0.2 kg is attached to the lower end of a massless spring of force constant 200Nm the other end of which is fixed to a rigid support. Study the following statements.
View SolutionTwo identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in the figure. The time period of oscillation is

View Solution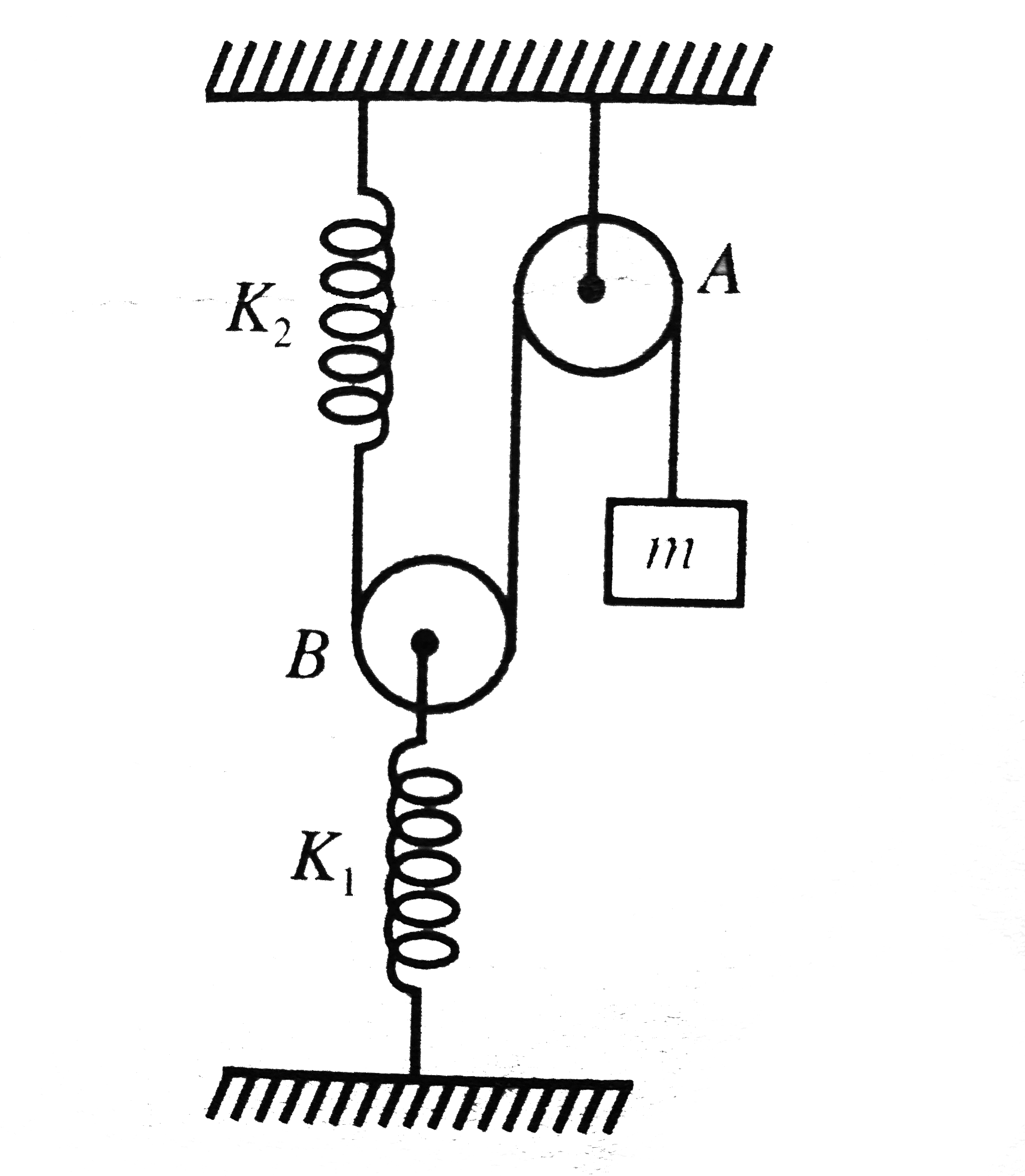
A block of mass m is tied to one end of a spring which passes over a smooth fixed pulley A and under a light smooth movable pulley B. The other end of the string is attached to the lower end of a spring of spring constant K2. Find the period of small oscillation of mass m about its equilibrium position (in second). (Take m=π2kg,K2k=4K1,K1=17Nm.)
View SolutionOn a smooth inclined plane a body of mass M is attached between two springs. The other ends of the springs are fixed to firm supports. If each spring has a force constant k, the period of oscilation of the body is (assuming the spring as massless)
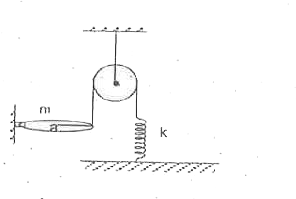
View SolutionThe string, spring and the pulley shown in figure are light. Find the time period of the mass m.

View SolutionA mass of 0.2 hg is attached to the lower end of a massles spring of force constant 200Nm the opper end of which is fixed to a rigid support. Study the following statements.
View SolutionA rod of length l and mass m, pivoted at one end, is held by a spring at its mid - point and a spring at far end. The spring have spring constant k. Find the frequency of small oscillations about the equilibrium position.

View Solution
