Two identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in the figure. The time period of oscillation is

2π√mk
2π√m2k
2π√2mk
π√m2k
The correct Answer is:B
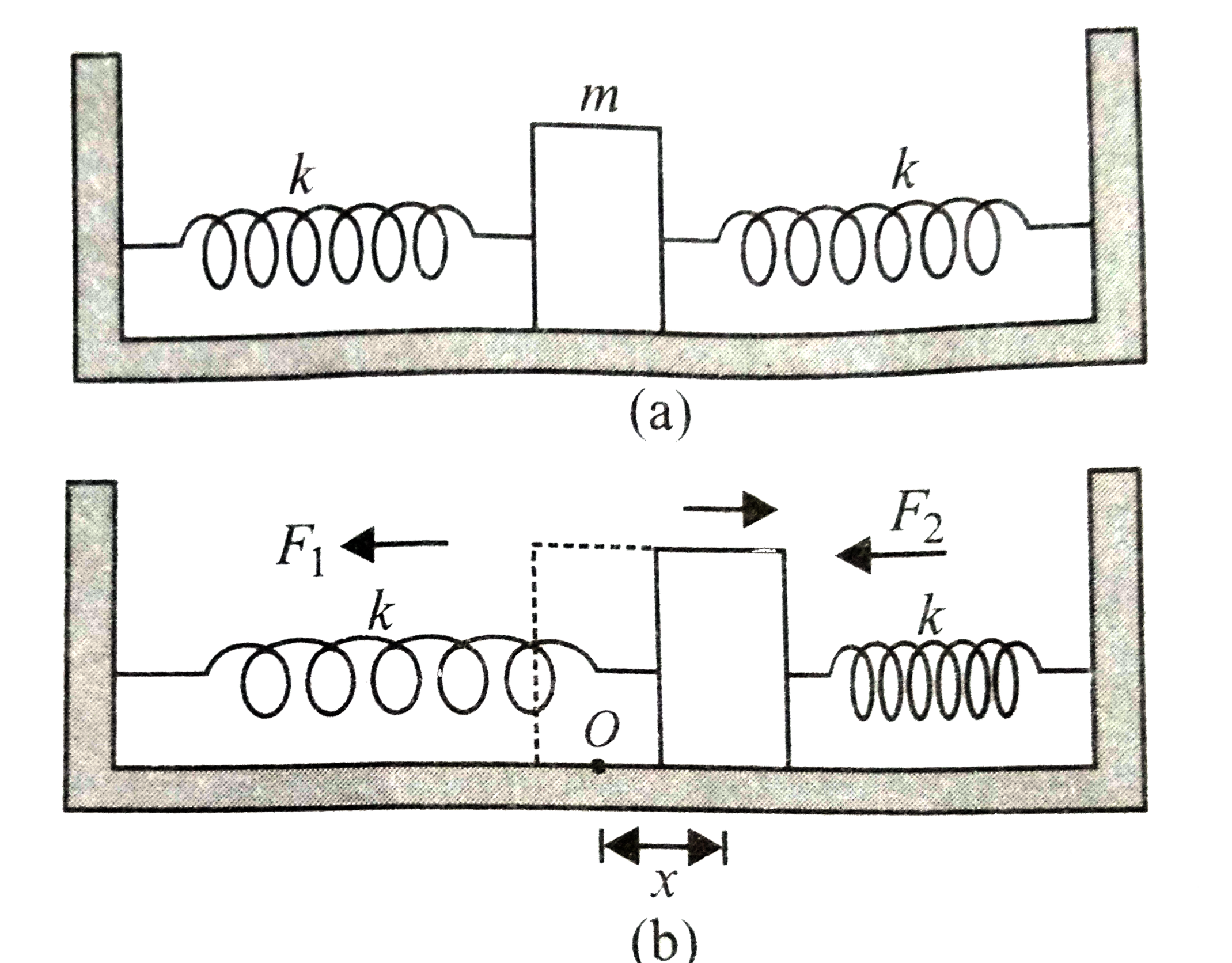
Let the mass m be displaced by a small distance x to the right from its mean position as shown in figure (b). Due to it’s the spring on the left side gets stretched by a length x while that on the right side gets compressed by the sae length. the forces acting on the mass are the same length. the forces acting on the mass are
F1=−kx towards left hand side
F2=−kx towards left hand side
The net force acting on the mass is, F=F1=−2kx
Here, F∝xand−ve sign shows that force is towards the mean position, therefore the motion executed by the particle is simple harmonic.
Its acceleration is
a=Fm=−2kxm . . . (i)
the standard equation of SHM is
a=−ω2x . . . (ii)
Comparing (i) and (ii), we get
ω2=2km or ω=√2km
time period, T=2πω=2π√m2k
Topper's Solved these Questions
- OSCILLATIONS Book:NCERT FINGERTPS ENGLISHChapter:OSCILLATIONS Exercise:Damped Simple Harmonic Motion
Explore 5 Videos
- OSCILLATIONS Book:NCERT FINGERTPS ENGLISHChapter:OSCILLATIONS Exercise:Forced Oscillation And Resonance
Explore 6 Videos
- OSCILLATIONS Book:NCERT FINGERTPS ENGLISHChapter:OSCILLATIONS Exercise:Energy In Simple Harmonic Motion
Explore 11 Videos
- MOTION IN A STRAIGHT LINEBook:NCERT FINGERTPS ENGLISHChapter:MOTION IN A STRAIGHT LINEExercise:NCERT Exemplar
Explore 6 Videos
- PHYSICAL WORLDBook:NCERT FINGERTPS ENGLISHChapter:PHYSICAL WORLDExercise:Assertion And Reason
Explore 10 Videos
Similar Questions
Tow identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in figure. When the mass is displaced from equilibrum position by a distance x towards right, find the restoring force.

View SolutionTwo identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in figure . Show that when the mass is displaced from its equilibrium position on either side, it executes a simple harmonic motion. Find the period of oscillation.

View SolutionTwo springs, each of spring constant k, are attached to a block of mass m as shown in the figure. The block can slide smoothly alongs a horizontal platform clamped to the oppsite walls of the trolley of mass M. If the block is displaced by xcm and released, the period of oscillaion is :

View Solution
A mass m is suspended from a spring of force constant k and just touches another identical spring fixed to the floor as shown in the fig. The time period of small oscillations is
View SolutionTwo identical springs of spring constant k each are connected in series and parallel as shown in figure. A mass M is suspended from them. The ratio of their frequencies of vertical oscillation will be
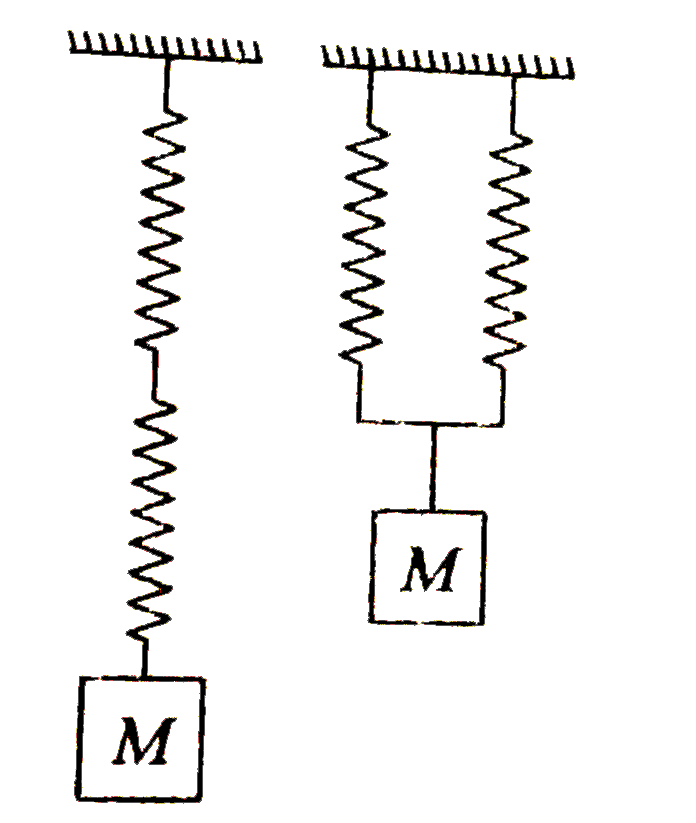
View Solution
A uniform rod of length l and mass M is pivoted at the centre. Its two ends are attached to two ends are attached to two springs of equal spring constant k. the springs are fixed to rigid support as shown in figure and the rod is free to oscillate in the horizontal plane. the rod is gently pushed through a small angle θ in one direction and released. the frequency of oscillation is
View SolutionAn object suspended from a spring exhibits oscillations of period T. Now ,the spring is cut in half and the two halves are used to support the same object, as shown in figure. The new period of oscillation is .
 .
.
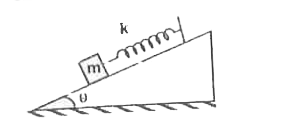
View SolutionA block of mass m can slide along a frictionless inclined plane, is attached to a ideal spring of spring constant as shown in the figure. Find the period of its oscillation. (Frame of reference attached to the wedge is at rest)
View SolutionA block of mass m is connected with two ideal pullies and a massless spring of spring constant K as shown in figure. The block is slightly displaced from its equilibrium position. If the time period of oscillation is μπ√mK. Then find the value of μ.

View SolutionA spring of spring constant k is cut into n equal parts, out of which r parts are placed in parallel and connected with mass M as shown in figure. The time period of oscillatory motion of mass M is:

View Solution