A sphere fo mass m makes SHM in a hemispherical bowl ABC and it moves from A to C and back to A via ABC, so that PB = h. If acceleration due to gravity is g, the speed of the ball when it just crosses the point B is
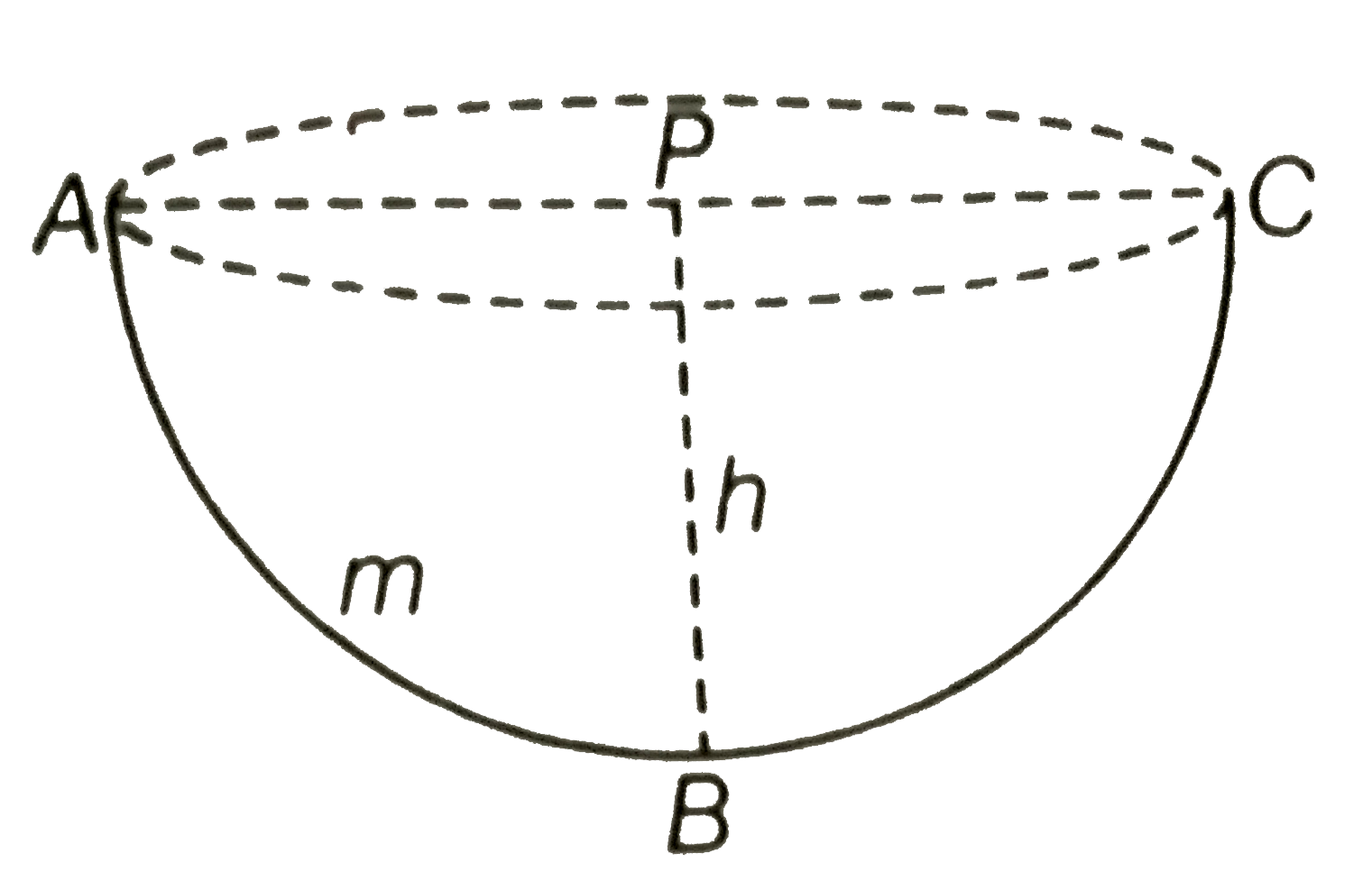
2gh
mgh
√2gh
gh2
The correct Answer is:C
Potential energy at A is converted into K.E. at B
∴mgh=12mv2B,V2B=2gh,vB=√2gh
Topper's Solved these Questions
- OSCILLATIONS BOOK - NCERT FINGERTPS ENGLISHCHAPTER - OSCILLATIONS EXERCISE - Damped Simple Harmonic Motion
5 Videos
- OSCILLATIONS BOOK - NCERT FINGERTPS ENGLISHCHAPTER - OSCILLATIONS EXERCISE - Forced Oscillation And Resonance
6 Videos
- OSCILLATIONS BOOK - NCERT FINGERTPS ENGLISHCHAPTER - OSCILLATIONS EXERCISE - Energy In Simple Harmonic Motion
11 Videos
- MOTION IN A STRAIGHT LINEBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - NCERT Exemplar
6 Videos
- PHYSICAL WORLDBOOK - NCERT FINGERTPS ENGLISHCHAPTER - PHYSICAL WORLDEXERCISE - Assertion And Reason
10 Videos
Similar Questions
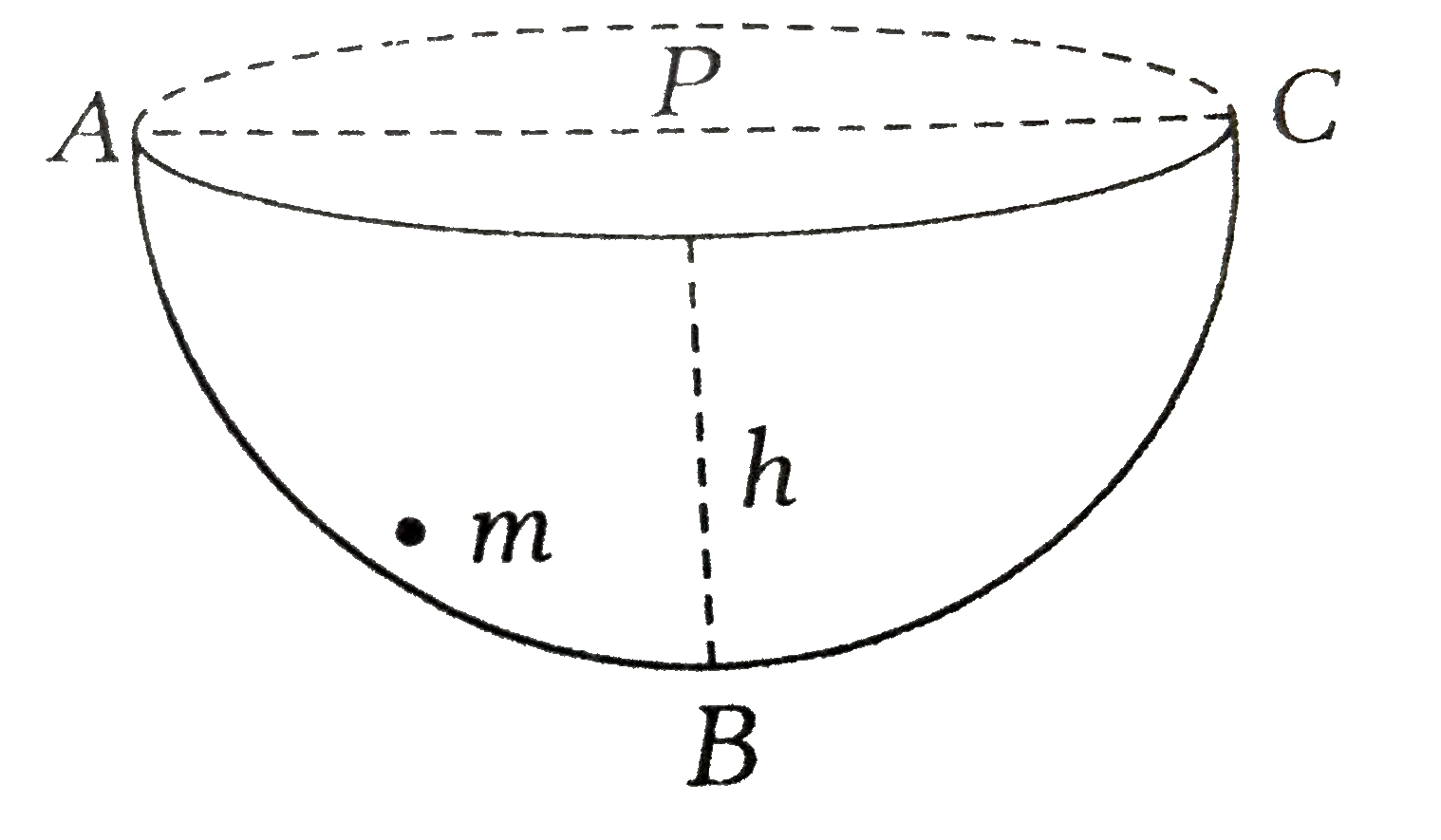
A particle of mass m makes SHM in a smooth hemispherical bowl ABC and it moves from A to C and back to A via ABC,so that PB=h. Find the speed of the ball when it just crosses the point B.
View SolutionThe condition for a uniform spherical mass m of a radius r to be a black hole is [G =gravitational constant and g=acceleration due to gravity]
View Solution
Knowledge Check
A simple pendulum with a bob of mass m oscillates from A to C and back to A such that PB is H. IF the acceleration due to gravity is g, the velocity of bob as it passes through B is
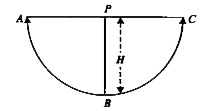 AzeroB2g HCmghD√(2gH)
AzeroB2g HCmghD√(2gH)
When you move from equator to pole, the value of acceleration due to gravity (g) :-
View SolutionIf the earth were to spin faster, acceleration due to gravity at the poles :
View SolutionAssuming the earth to be a sphere of uniform density, the acceleration due to gravity
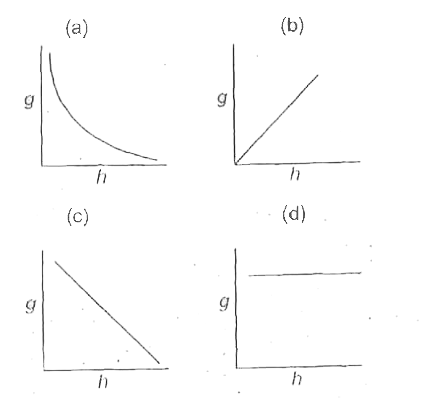
View SolutionWhich of the following graphs shows the variation of acceleration due to gravity g with depth h from the surface of the earth ?
View SolutionA satellite of mass m is moving in a circular or orbit of radius R around the earth. The radius of the earth is r and the acceleration due to gravity at the surface of the earth is g. Obtain expressions for the following :
(a) The acceleration due to gravity at a distance R from the centre of the earth
(b) The linear speed of the satellite
(c ) The time period of the satellite
View SolutionA : The acceleration due to gravity for an is independent from its mass.
R : The value of 'g ' depends on the mass of planet .
View SolutionA satellite of mass m revolves around the earth of radius R at a hight x from its surface. If g is the acceleration due to gravity on the surface of the earth, the orbital speed of the satellite is
View Solution
