A simple pendulum executing SHM with a period of 6 s between two extreme positions B and C about a point O. if the length of the arc BC is 10 cm, how long will the pendulum take the move from position C to a position D towards O exactly midway between C and O?
0.5 s
1 s
1.5 s
3 s
The correct Answer is:B
To solve the problem, we need to determine the time it takes for a simple pendulum to move from position C to position D, which is exactly midway between position O (the mean position) and position C. Here’s a step-by-step breakdown of the solution:
Step 1: Identify the given information
- The period (T) of the pendulum is 6 seconds.
- The length of the arc BC is 10 cm.
- The mean position O is the midpoint of the arc BC.
Step 2: Calculate the amplitude of the pendulum
The amplitude (A) is half the length of the arc BC. Therefore:
A=BC2=10 cm2=5 cm
Step 3: Determine the position of point D
Point D is midway between O and C. Since the distance from O to C is equal to the amplitude (5 cm), the distance from O to D is:
OD=OC2=5 cm2=2.5 cm
Step 4: Use the formula for displacement in SHM
The displacement (x) at any time (t) can be expressed as:
x=Acos(ωt)
where ω is the angular frequency given by:
ω=2πT
Substituting the period:
ω=2π6=π3
Step 5: Set up the equation for position D
At position D, the displacement (x) is 2.5 cm. Therefore, we can write:
2.5=5cos(π3t)
Dividing both sides by 5 gives:
12=cos(π3t)
Step 6: Solve for π3t
The cosine of π3 is 12, so:
π3t=π3
Step 7: Solve for time (t)
To find t, we can cancel π from both sides:
t=1 second
Conclusion
The time taken for the pendulum to move from position C to position D is 1 second.
---
- The period (T) of the pendulum is 6 seconds.
- The length of the arc BC is 10 cm.
- The mean position O is the midpoint of the arc BC.
The amplitude (A) is half the length of the arc BC. Therefore:
A=BC2=10 cm2=5 cm
Point D is midway between O and C. Since the distance from O to C is equal to the amplitude (5 cm), the distance from O to D is:
OD=OC2=5 cm2=2.5 cm
The displacement (x) at any time (t) can be expressed as:
x=Acos(ωt)
where ω is the angular frequency given by:
ω=2πT
Substituting the period:
ω=2π6=π3
At position D, the displacement (x) is 2.5 cm. Therefore, we can write:
2.5=5cos(π3t)
Dividing both sides by 5 gives:
12=cos(π3t)
The cosine of π3 is 12, so:
π3t=π3
To find t, we can cancel π from both sides:
t=1 second
The time taken for the pendulum to move from position C to position D is 1 second.
Topper's Solved these Questions
- OSCILLATIONS BOOK - NCERT FINGERTPS ENGLISHCHAPTER - OSCILLATIONS EXERCISE - Higher Order Thinking Skills
8 Videos
- OSCILLATIONS BOOK - NCERT FINGERTPS ENGLISHCHAPTER - OSCILLATIONS EXERCISE - Exemplar Problems
9 Videos
- MOTION IN A STRAIGHT LINEBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - NCERT Exemplar
6 Videos
- PHYSICAL WORLDBOOK - NCERT FINGERTPS ENGLISHCHAPTER - PHYSICAL WORLDEXERCISE - Assertion And Reason
10 Videos
Similar Questions
A particle executes SHM with amplitude of 20 cm and time period of 12 s. What is the minimum time required for it to move between two points 10 cm on either side of the mean position?
View SolutionName the type of energy possessed by the bob of a simple pendulum when it is at (a) the extreme position, (b) the mean position, and (c) between the mean and extreme positions
View Solution
Knowledge Check
A particle is executing simple harmonic motion of amplitude 5 cm and period 6 s. How long will it take to move from one end of its path on one side of mean position to a position 2.5 cm on the same side of the mean position ?
A1 sB1.5 sC3 sD3.5 s
A source of sound attached to the bob of a simple pendulum execute SHM . The difference between the apparent frequency of sound as received by an observer during its approach and recession at the mean frequency of the source . The velocity of the source at the mean position is ( velocity of sound in the air is 340m/s)
[Assume velocity of sound << velocity of sound in air ]
View SolutionA simple pendulum executing SHM in a straight line has zero velocity at 'A' and 'B' whose distances form 'O' in the same line OAB are 'a' and 'b'. If the velocity half way between them is 'v' then its time period is
View SolutionA particle executing SHM oscillates between two fixed points separated by 20cm . If its maximum velocity be 30cm/s. Find its velocity when its displacement is 5cm from its mean position.
View SolutionThe figure below shows a simple pendulum of mass 200 g. It is displaced from the mean position A to the extreme position B. The potential energy at the position A is zero. At the position B the pendulum bob is raised by 5 m.
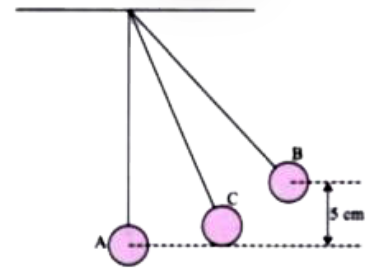
(i) What is the potential energy of the pendulum at the position B?
(ii) What is the total mechanical energy at point C?
(iii) What is the speed of the bob at the position A when released from B ?
(Take g = 10ms−2 and there is no loss of energy.)
View SolutionA pendulum with bob of mass is scillating on either side from its resting position A between the extremes B and Cala vertical height above A. What is the kinetic energy K and potential energy U when the pendulum is al positions (i) A. (ii) B. and (in C?
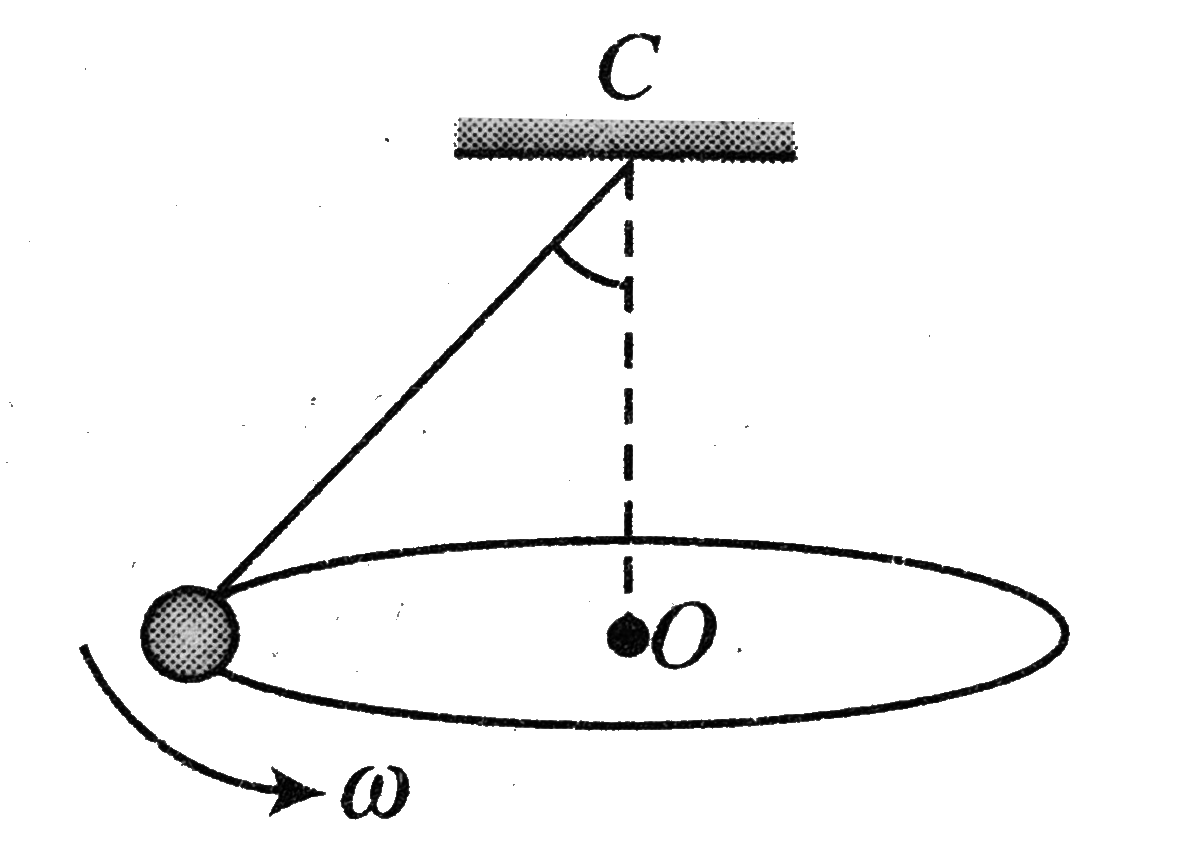
View SolutionA conical pendulum consists of a simple pendulum moving in a horizontal circle as shown in the figure. C is the pivot, O the centre of the circle in which the pendulum bob moves and ω the constant angular velocity of the bob. If →L is the angular momentum about point C, then
View SolutionA simple pendulum of length l and bob of mass m is displaced from its equilibrium position O to a position P so that hight of P above O is h . If is then released. What is the tension in the string when the bob passes through the through the equilibrium position O ? Neglect friction. v is the velocity of the bob at O
View Solution
