Assertion: A combination of two simple harmonic motions with a arbitrary amplitudes and phases is not necessarily periodic.
Reason: A periodic motion can always be expressed as a sum of infinite number of harmonic motions with appropriate amplitudes.
If both assertion and reson are true and reason is the correct explanation of assertion
If both assertion and reason are true but reason is not the correct explanation of assertion.
If assertion is true but reason is false.
If both assertion and reason are false.
The correct Answer is:B
To solve the question, we need to analyze both the assertion and the reason provided.
Step 1: Understand the Assertion
The assertion states that a combination of two simple harmonic motions (SHMs) with arbitrary amplitudes and phases is not necessarily periodic.
Explanation:
- For two SHMs to be periodic when combined, their frequencies must have a specific relationship. Specifically, if the frequency of one SHM is an integral multiple of the other, the combination will be periodic. If not, the combination may not repeat itself after a fixed interval, hence not periodic.
Step 2: Understand the Reason
The reason states that a periodic motion can always be expressed as a sum of an infinite number of harmonic motions with appropriate amplitudes.
Explanation:
- This statement is true in the context of Fourier series, where any periodic function can be represented as a sum of sine and cosine functions (harmonic motions). However, this does not directly explain why the assertion is true.
Step 3: Determine the Truth of Each Statement
- The assertion is true because the combination of two SHMs is periodic only under certain conditions (integral multiple of frequencies).
- The reason is also true, but it does not provide a correct explanation for the assertion.
Step 4: Conclusion
Since both the assertion and the reason are true, but the reason does not correctly explain the assertion, the correct answer is that both are true, but the reason is not a correct explanation of the assertion.
Final Answer:
The correct option is B: Both assertion and reason are true, but the reason is not a correct explanation of the assertion.
---
The assertion states that a combination of two simple harmonic motions (SHMs) with arbitrary amplitudes and phases is not necessarily periodic.
- For two SHMs to be periodic when combined, their frequencies must have a specific relationship. Specifically, if the frequency of one SHM is an integral multiple of the other, the combination will be periodic. If not, the combination may not repeat itself after a fixed interval, hence not periodic.
The reason states that a periodic motion can always be expressed as a sum of an infinite number of harmonic motions with appropriate amplitudes.
- This statement is true in the context of Fourier series, where any periodic function can be represented as a sum of sine and cosine functions (harmonic motions). However, this does not directly explain why the assertion is true.
- The assertion is true because the combination of two SHMs is periodic only under certain conditions (integral multiple of frequencies).
- The reason is also true, but it does not provide a correct explanation for the assertion.
Since both the assertion and the reason are true, but the reason does not correctly explain the assertion, the correct answer is that both are true, but the reason is not a correct explanation of the assertion.
The correct option is B: Both assertion and reason are true, but the reason is not a correct explanation of the assertion.
Topper's Solved these Questions
- OSCILLATIONS BOOK - NCERT FINGERTPS ENGLISHCHAPTER - OSCILLATIONS EXERCISE - Periodic And Oscillatory Motions
7 Videos
- OSCILLATIONS BOOK - NCERT FINGERTPS ENGLISHCHAPTER - OSCILLATIONS EXERCISE - Simple Harmonic Motion
17 Videos
- OSCILLATIONS BOOK - NCERT FINGERTPS ENGLISHCHAPTER - OSCILLATIONS EXERCISE - Exemplar Problems
9 Videos
- MOTION IN A STRAIGHT LINEBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - NCERT Exemplar
6 Videos
- PHYSICAL WORLDBOOK - NCERT FINGERTPS ENGLISHCHAPTER - PHYSICAL WORLDEXERCISE - Assertion And Reason
10 Videos
Similar Questions
Knowledge Check
A particle executing simple harmonic motion with an amplitude A. The distance travelled by the particle in one time period is
AzeroBAC2AD4AThe time period of simple harmonic motion depends upon
AamplitudeBenergyCphase constantDmassAssertion: The motion of the earth around the sun is perriodic but not oscillatory.
Reason: Oscillatory motion is necessarily periodic but periodic motion is not necessarily oscillatory.AIf both assertion and reson are true and reason is the correct explanation of assertionBIf both assertion and reason are true but reason is not the correct explanation of assertion.CIf assertion is true but reason is false.DIf both assertion and reason are false.
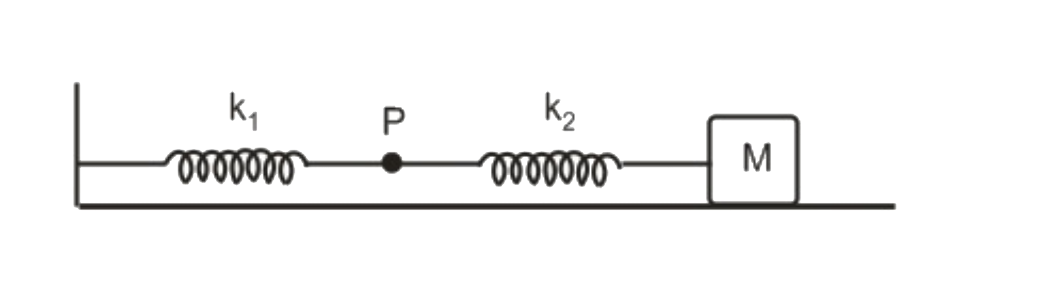
The mass M shown in figure ocillates in simple harmonic motion with amplitude A.
The amplitude of the point P is
View SolutionThe phase (at a time t) of a particle in simple harmonic motion tells
View SolutionA particle executing of a simple harmonic motion covers a distance equal to half its amplitude in on e second . Then the time period of the simple harmonic motion is
View SolutionThe average energy in one time period in simple harmonic motion is
View SolutionA particle is executing simple harmonic motion with an amplitude A and time period T. The displacement of the particles after 2T period from its initial position is
View Solution
