Assertion: A block of small mass m attached to a stiff spring will have large oscillation frequency.
Reason: Stiff springs have high value of spring constant.
If both assertion and reson are true and reason is the correct explanation of assertion
If both assertion and reason are true but reason is not the correct explanation of assertion.
If assertion is true but reason is false.
If both assertion and reason are false.
The correct Answer is:A
Angular frequency, ω=√km as stiff springs have high value of k, so that block will oscillate with large oscillation frequency.
Topper's Solved these Questions
- OSCILLATIONS BOOK - NCERT FINGERTPS ENGLISHCHAPTER - OSCILLATIONS EXERCISE - Periodic And Oscillatory Motions
7 Videos
- OSCILLATIONS BOOK - NCERT FINGERTPS ENGLISHCHAPTER - OSCILLATIONS EXERCISE - Simple Harmonic Motion
17 Videos
- OSCILLATIONS BOOK - NCERT FINGERTPS ENGLISHCHAPTER - OSCILLATIONS EXERCISE - Exemplar Problems
9 Videos
- MOTION IN A STRAIGHT LINEBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - NCERT Exemplar
6 Videos
- PHYSICAL WORLDBOOK - NCERT FINGERTPS ENGLISHCHAPTER - PHYSICAL WORLDEXERCISE - Assertion And Reason
10 Videos
Similar Questions
Derive an experession for the period of oscillation of a mass attached to a spring executing simple harmonic motion. Given that the period of oscillation depends on the mass m and the force constant k, where k is the force required to stretch the spring by unit length?
View SolutionIn the figure, the block of mass m, attached to the spring of stiffness k is in correct with the completely elastic wall, and the compression in the spring is e. The spring is compressed further by e by displacing the block towards left and is then released. If the collision between the block and the wall is completely eleastic then the time period of oscillation of the block will be

View Solution
Knowledge Check
A body of mass 20 g connected to a spring of spring constant k, executes simple harmonic motion with a frequency of (5/π) Hz. The value of spring constant is
A4Nm−1B3Nm−1C2Nm−1D5Nm−1On a smooth inclined plane, a body of mass M is attached between two springs. The other ends of the springs are fixed to firm supports. If each spring has force constant K , the period of oscillation of the body (assuming the springs as massless) is
 A1. 2π√M2kB2. 2π√2MkC3. 2π√Mgsinθ2kD4. 2π√2Mgk
A1. 2π√M2kB2. 2π√2MkC3. 2π√Mgsinθ2kD4. 2π√2Mgk
Find the time period of oscillation of block of mass m. Spring, and pulley are ideal. Spring constant is k.
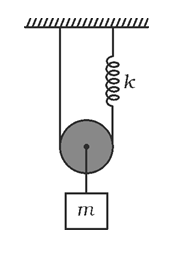
View SolutionA mass M=5 kg is attached to a string as shown in the figure and held in position so that the spring remains unstretched. The spring constant is 200Nm−1 . The mass M is then released and begins to undergo small oscillations. The amplitude of oscillation is
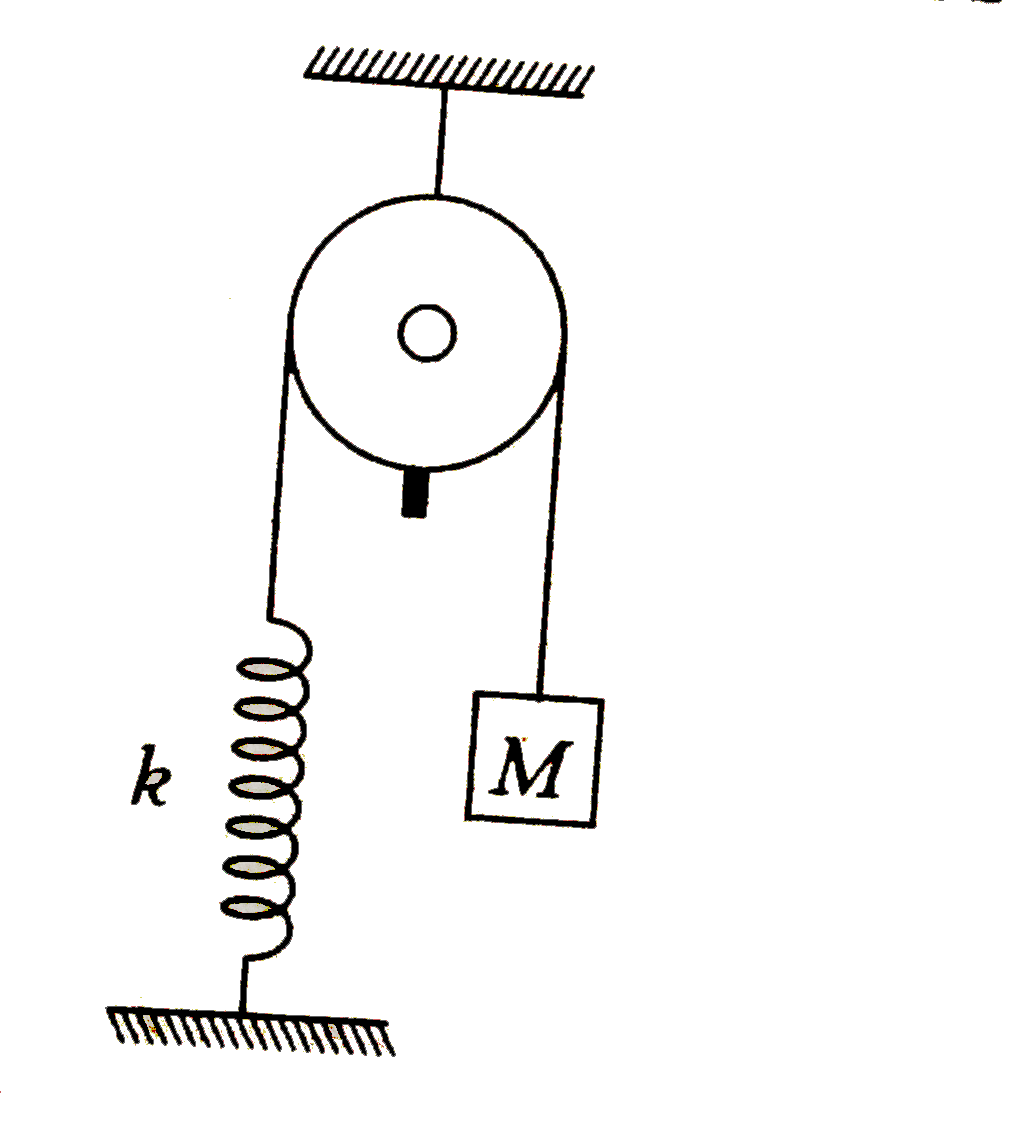
View SolutionA block of mass m is attached to three springs A,B and C having force constants k,k and 2k respectively as shown in figure. If the block is slightly oushed against spring C. If the angular frequency of oscillations is √Nkm, then find N. The system is placed on horizontal smooth surface.
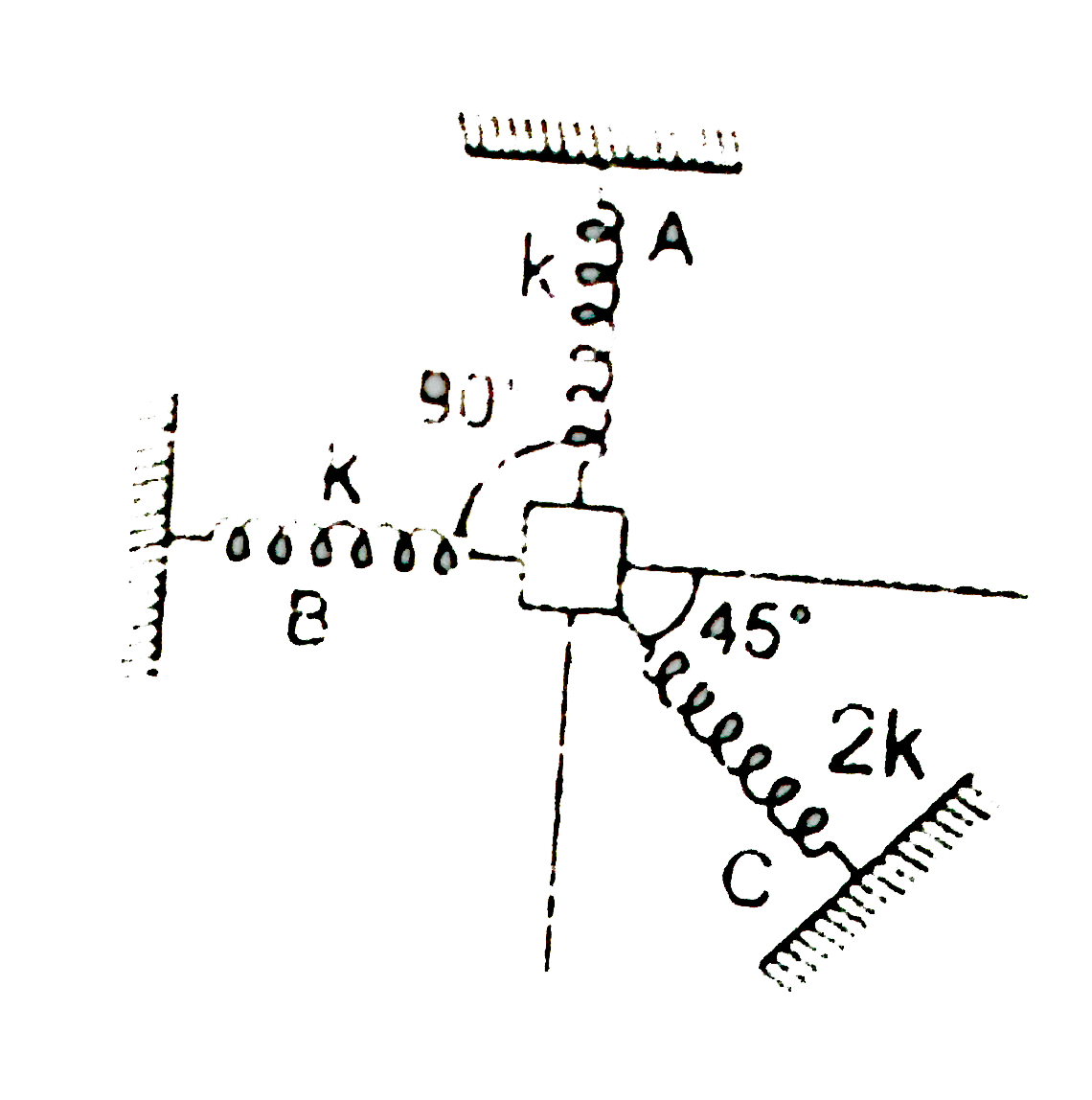
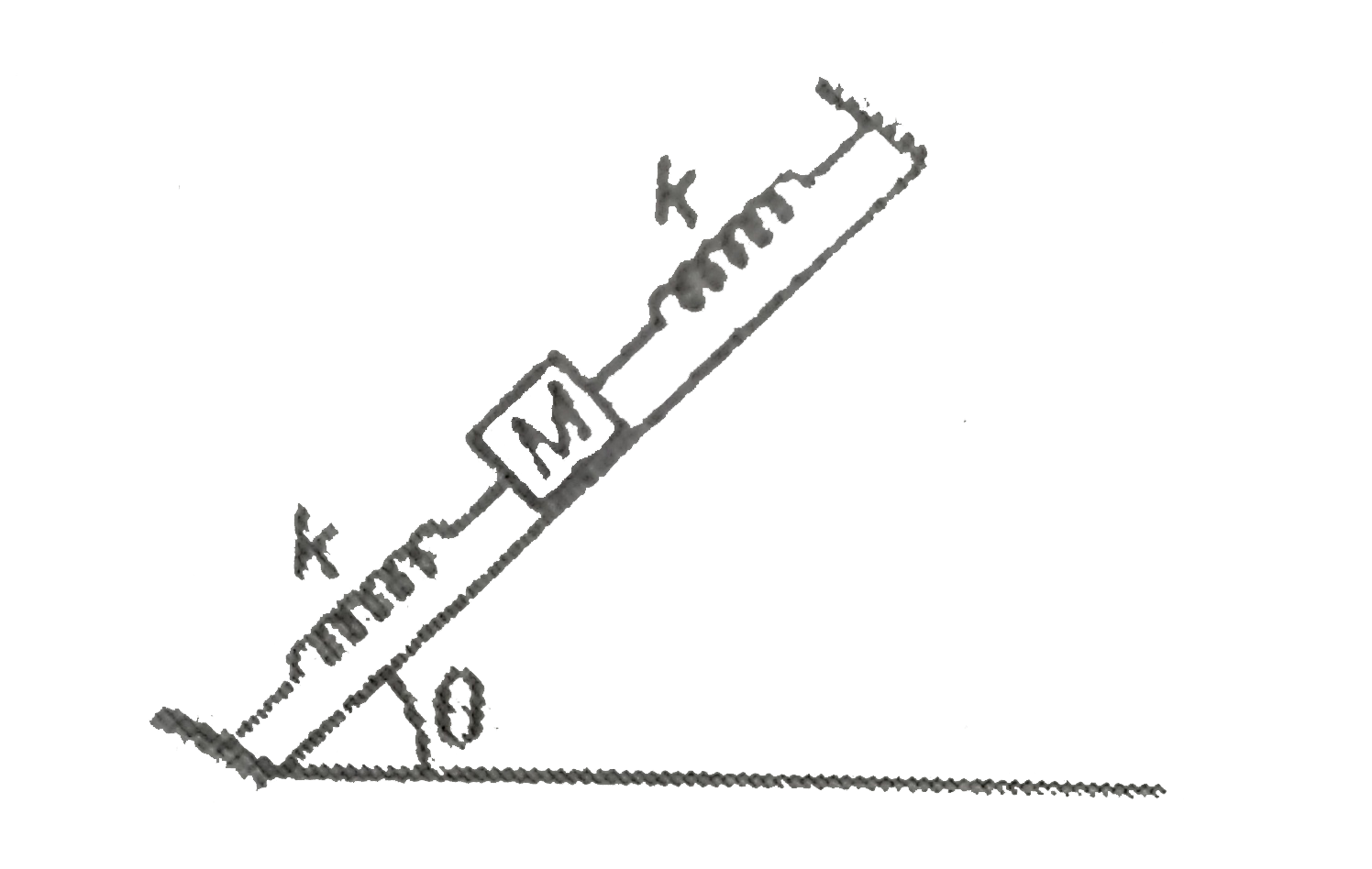
View SolutionOn a smooth inclined plane a body of mass M is attached between two springs. The other ends of the springs are fixed to firm supports. If each spring has a force constant k, the period of oscilation of the body is (assuming the spring as massless)
View SolutionA block of mass m is attached to one end of a mass less spring of spring constant k. the other end of spring is fixed to a wall the block can move on a horizontal rough surface. The coefficient of friction between the block and the surface is μ then the compession of the spring for which maximum extension of the spring becomes half of maximum compression is .
View SolutionIn a spring- mass system , the length of the spring is L, and it has a mass M attached to it and oscillates with an angular frequency ω. The spring is then cut into two parts, one (i) with relaxed length αL and the other (ii) with relaxed length (1−α) L. The force constants of the two spring A and B are
View Solution
