A body of mass 20 g connected to a spring of spring constant k, executes simple harmonic motion with a frequency of Hz. The value of spring constant is
The correct Answer is:C
To find the spring constant k for a body executing simple harmonic motion, we can use the formula relating frequency f, mass m, and spring constant k.
1. Identify the given values:
- Mass m=20g=20×10−3kg=0.02kg
- Frequency f=5πHz
2. Use the formula for frequency in terms of mass and spring constant:
f=12π√km
3. Rearranging the formula to solve for k:
k=(2πf)2m
4. Substituting the values into the equation:
- First, calculate 2πf:
2πf=2π(5π)=10
- Now substitute 10 into the equation for k:
k=(10)2⋅0.02
5. Calculate k:
k=100⋅0.02=2N/m
Conclusion:
The value of the spring constant k is 2N/m.
---
- Mass m=20g=20×10−3kg=0.02kg
- Frequency f=5πHz
f=12π√km
k=(2πf)2m
- First, calculate 2πf:
2πf=2π(5π)=10
- Now substitute 10 into the equation for k:
k=(10)2⋅0.02
k=100⋅0.02=2N/m
The value of the spring constant k is 2N/m.
Topper's Solved these Questions
- OSCILLATIONS Book:NCERT FINGERTPS ENGLISHChapter:OSCILLATIONS Exercise:Higher Order Thinking Skills
Explore 8 Videos
- OSCILLATIONS Book:NCERT FINGERTPS ENGLISHChapter:OSCILLATIONS Exercise:Exemplar Problems
Explore 9 Videos
- MOTION IN A STRAIGHT LINEBook:NCERT FINGERTPS ENGLISHChapter:MOTION IN A STRAIGHT LINEExercise:NCERT Exemplar
Explore 6 Videos
- PHYSICAL WORLDBook:NCERT FINGERTPS ENGLISHChapter:PHYSICAL WORLDExercise:Assertion And Reason
Explore 10 Videos
Similar Questions
Knowledge Check
A mass of 1 kg suspended from a spring whose force constant is 400 Nm−1, executes simple harmonic motion. When the energy of the oscillator is 2J, the maximum acceleration experienced by maas will be
A2ms−2B4ms−2C40ms−2D400ms−2Assertion: A block of small mass m attached to a stiff spring will have large oscillation frequency.
Reason: Stiff springs have high value of spring constant.AIf both assertion and reson are true and reason is the correct explanation of assertionBIf both assertion and reason are true but reason is not the correct explanation of assertion.CIf assertion is true but reason is false.DIf both assertion and reason are false.
A body of mass m attached to one end of an ideal spring of force constant k is executing simple harmonic motion. Establish that the time - period of oscillation is T=2π√m/k.
View SolutionA particle of mass 3 kg , attached to a spring with force constant 48Nm−1execute simple harmonic motion on a frictionless horizontal surface. The time period of oscillation of the particle, is seconds , is
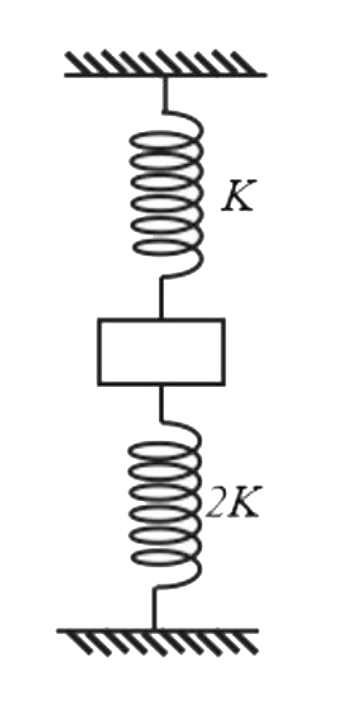
View SolutionA block of mass m is connected two springs of spring constant 2k annd k , respectively , as shown in the vertical plane. At equilibrium , both springs are compressed by same length. If suddenly lower spring is cut, then acceleration of block, just after spring cut , is
View SolutionA body of mass m hung at one end of the spring executes simple harmonic motion . The force constant of a spring is k while its period of vibration is T. Prove by dimensional method that the equation T=2π√m/k is correct. Dervive the correct equation , assuming that they are related by a power law.
View SolutionA body of mass 2 kg suspended through a vertical spring executes simple harmonic motionof period 4s. If the oscillations are stopped and the body hangs in equillibrium, find the potential energy stored in the spring.
View SolutionA man weighing 60kg stands on the horizontal platform of a spring balance. The platform starts executing simple harmonic motion of amplitude 0.1m and frequency 2π. its which of the following statement is correct ?

View Solution