A spring of spring constant k is cut into n equal parts, out of which r parts are placed in parallel and connected with mass M as shown in figure. The time period of oscillatory motion of mass M is:

T=2π√MrnK
T=2π√nrMK
T=2π√nMnK
T=2π√nMrK
The correct Answer is:A
K.I=k'×In constant
new spring constand for each part is k'=nK
Now r part are taken in parallel.
so Keq=nrk, Time period =2π√MKeq=2π√MnrK
Topper's Solved these Questions
- SIMPLE HARMONIC MOTION BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - LEVEL (2)
40 Videos
- SIMPLE HARMONIC MOTION BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - 6-previous year question
56 Videos
- SIMPLE HARMONIC MOTION BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - LEVEL 0 LONG ANSWER TYPE
2 Videos
- ROTATIONAL MOTION BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - JEE Advanced (Archive) (True/False Type)
3 Videos
- SYSTEM OF A PARTICLES & ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF A PARTICLES & ROTATIONAL MOTIONEXERCISE - IN-CHAPTER EXERCISE F
10 Videos
Similar Questions
Knowledge Check
A system of springs with their spring constants are as shown in figure. What is the frequency of oscillations of the mass m ?
 A12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k4]mB12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k2]mC12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k2]mD12π√(k1+k2)(k3+k4)+k1k2k1k2(k3+k4)m
A12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k4]mB12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k2]mC12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k2]mD12π√(k1+k2)(k3+k4)+k1k2k1k2(k3+k4)m
A spring of force constant 'k' is cut into four equal parts one part is attached with a mass m. The time period of oscillation will be
View SolutionTwo identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in the figure. The time period of oscillation is

View SolutionIf a spring has time period T, and is cut into (n) equal parts, then the time period of each part will be.
View Solution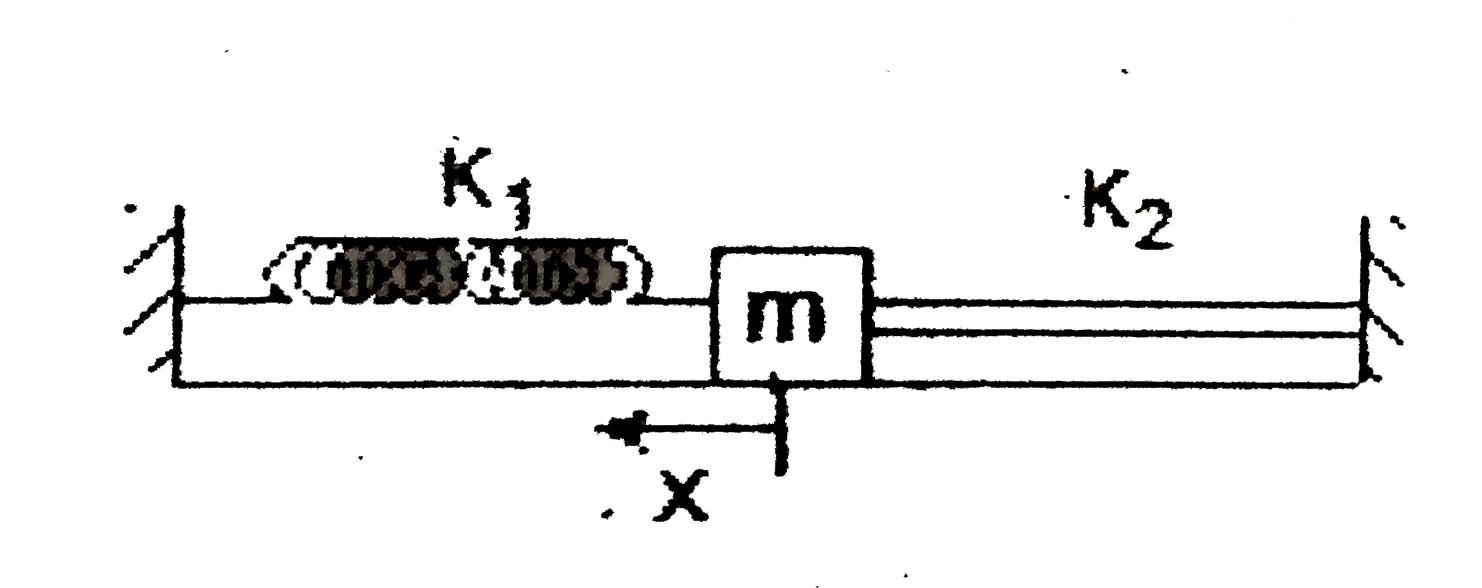
A block of mass is connected to an ideal spring of stiffness K1 on left hand side and to an elastic strig of stiffness K2 on right hand side as shown in figure the time period of motion if mass m is displaced by 'x' as shown in figure.
View Solution
A mass m is suspended from a spring of force constant k and just touches another identical spring fixed to the floor as shown in the fig. The time period of small oscillations is
View SolutionA body of mass m is suspended from three springs as shown in figure. If mass m is displaced slightly then time period of oscillation is

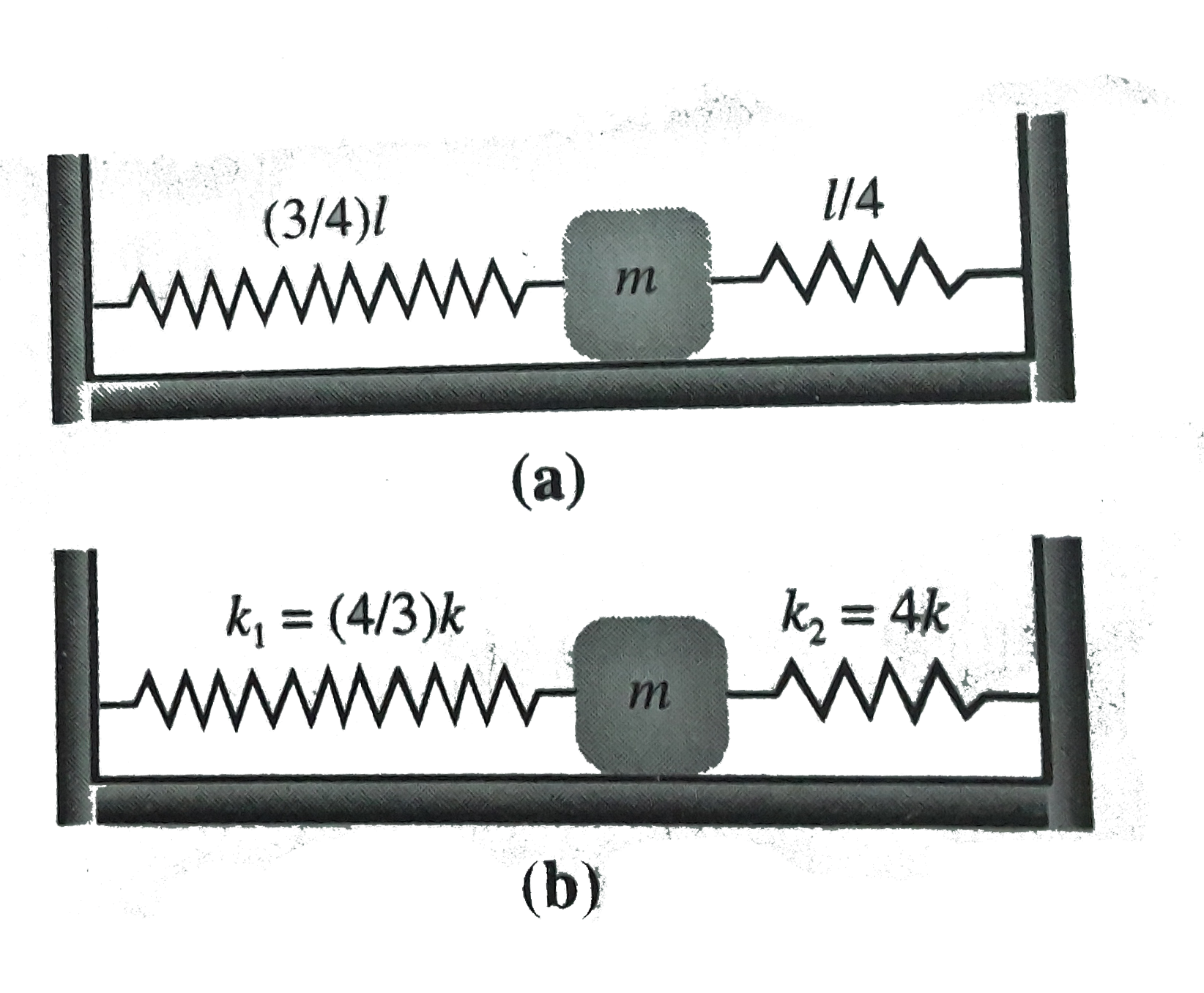
View SolutionA spring of stiffness constant k and natural length l is cut into two parts of length 3l/4andl/4, respectively, and an arrangement is made as shown in figure . If the mass is slightly displaced , find the time period of oscillation.
View Solution

