An ice-cube of edge is 10 cm floating in water. Time period of small vertical oscillations of the cube is: (Specific gravity of ice is 0.9)
(a)0.6s
(b)1.6s
(c)2.4s
(d)3.6s
The correct Answer is:A
To solve the problem of finding the time period of small vertical oscillations of an ice cube floating in water, we can follow these steps:
Step 1: Understand the Given Information
- The edge of the ice cube is a=10cm=0.1m.
- The specific gravity of ice is SG=0.9.
- The density of water is ρw=1000kg/m3.
- The density of ice can be calculated as:
ρi=SG×ρw=0.9×1000kg/m3=900kg/m3.
Step 2: Calculate the Effective Density
The effective density for the oscillation can be derived from the ratio of the density of the ice to the density of water:
ρiρw=9001000=0.9.
Step 3: Use the Formula for Time Period of Vertical Oscillation
The formula for the time period T of small vertical oscillations of a floating object is given by:
T=2π√hg,
where h is the depth of the submerged part of the ice cube and g is the acceleration due to gravity.
Step 4: Calculate the Submerged Depth
The volume of the ice cube is:
V=a3=(0.1)3=0.001m3.
The weight of the ice cube is equal to the weight of the water displaced:
Weight of ice=ρi⋅V⋅g=900⋅0.001⋅10=9N.
The volume of water displaced Vd is:
Vd=Weight of iceρw⋅g=91000⋅10=0.0009m3.
The submerged depth h can be calculated from the volume of water displaced:
h=Vda2=0.0009(0.1)2=0.00090.01=0.09m.
Step 5: Substitute Values into the Time Period Formula
Now substituting the values into the time period formula:
T=2π√0.0910.
Calculating the square root:
√0.0910=√0.009=0.03.
Thus,
T=2π⋅0.03=0.06π≈0.1884s.
Step 6: Final Calculation
To convert to seconds:
T≈0.1884s≈0.6s (after rounding).
Conclusion
The time period of small vertical oscillations of the ice cube is approximately 0.6s.
- The edge of the ice cube is a=10cm=0.1m.
- The specific gravity of ice is SG=0.9.
- The density of water is ρw=1000kg/m3.
- The density of ice can be calculated as:
ρi=SG×ρw=0.9×1000kg/m3=900kg/m3.
The effective density for the oscillation can be derived from the ratio of the density of the ice to the density of water:
ρiρw=9001000=0.9.
The formula for the time period T of small vertical oscillations of a floating object is given by:
T=2π√hg,
where h is the depth of the submerged part of the ice cube and g is the acceleration due to gravity.
The volume of the ice cube is:
V=a3=(0.1)3=0.001m3.
The weight of the ice cube is equal to the weight of the water displaced:
Weight of ice=ρi⋅V⋅g=900⋅0.001⋅10=9N.
The volume of water displaced Vd is:
Vd=Weight of iceρw⋅g=91000⋅10=0.0009m3.
The submerged depth h can be calculated from the volume of water displaced:
h=Vda2=0.0009(0.1)2=0.00090.01=0.09m.
Now substituting the values into the time period formula:
T=2π√0.0910.
Calculating the square root:
√0.0910=√0.009=0.03.
Thus,
T=2π⋅0.03=0.06π≈0.1884s.
To convert to seconds:
T≈0.1884s≈0.6s (after rounding).
The time period of small vertical oscillations of the ice cube is approximately 0.6s.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTION Book:VMC MODULES ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:LEVEL (2)
Explore 40 Videos
- SIMPLE HARMONIC MOTION Book:VMC MODULES ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:6-previous year question
Explore 56 Videos
- SIMPLE HARMONIC MOTION Book:VMC MODULES ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:LEVEL 0 LONG ANSWER TYPE
Explore 2 Videos
- ROTATIONAL MOTION Book:VMC MODULES ENGLISHChapter:ROTATIONAL MOTION Exercise:JEE Advanced (Archive) (True/False Type)
Explore 3 Videos
- SYSTEM OF A PARTICLES & ROTATIONAL MOTIONBook:VMC MODULES ENGLISHChapter:SYSTEM OF A PARTICLES & ROTATIONAL MOTIONExercise:IN-CHAPTER EXERCISE F
Explore 10 Videos
Similar Questions
A block of ice of total area A and thicknes 0.5m is floating in water. In order to just support a man of nass 100kg, the area A should be (the specific gravity of ice is 0.9)
View SolutionA small ball is kept on the top of a sphere of radius R. The sphere start accelerating with constant acceleration of 10m/s2 horizontally. The angle of radial line with the vertical at which small ball leaves the sphere is 12sin−1(K/9). Find the value of K. [take g=10m/s2]
View Solution
Knowledge Check
Iceberg floats in sea water with a part of it submerged. The percentage fraction of the ice berg not submerged is (density of ice = 0.9gcm−3, density of sea water = 1.1gcm−3)
A18%B12%C10%D8%
A cube of ice of side length 10 cm is floating in water of density 1000 kg/m3. Then pick up the correct statement (density of ice = 900 kg/m3)
View SolutionAn ice cube of side 1cm is floating at the interface of kerosene and water in a beaker of base area 10cm2. The level of kerosene is just covering the top surface of the ice cube.
a. Find the depth of submergence in the kerosene and that in the water.
b. Find the change in the total level of the liquid when the whole ice melts into water.

View SolutionAn ice cube floats in water. What percentage of volume is outside water. Density of water =1g/cc, density of ice =0.9g/cc.
View SolutionAn ice cube of size a=10cm is floating in a tank (base area A=50cm×50cm) partially filled with water. The change in gravitational potential energy, when ice melts completely is (density of ice is 900kg/m2)
View SolutionAn ice cube is floating in water above which a layer of a fighter oil is poured. As the ice melts completely, the level If water surface (or interface) and upper level of oil will
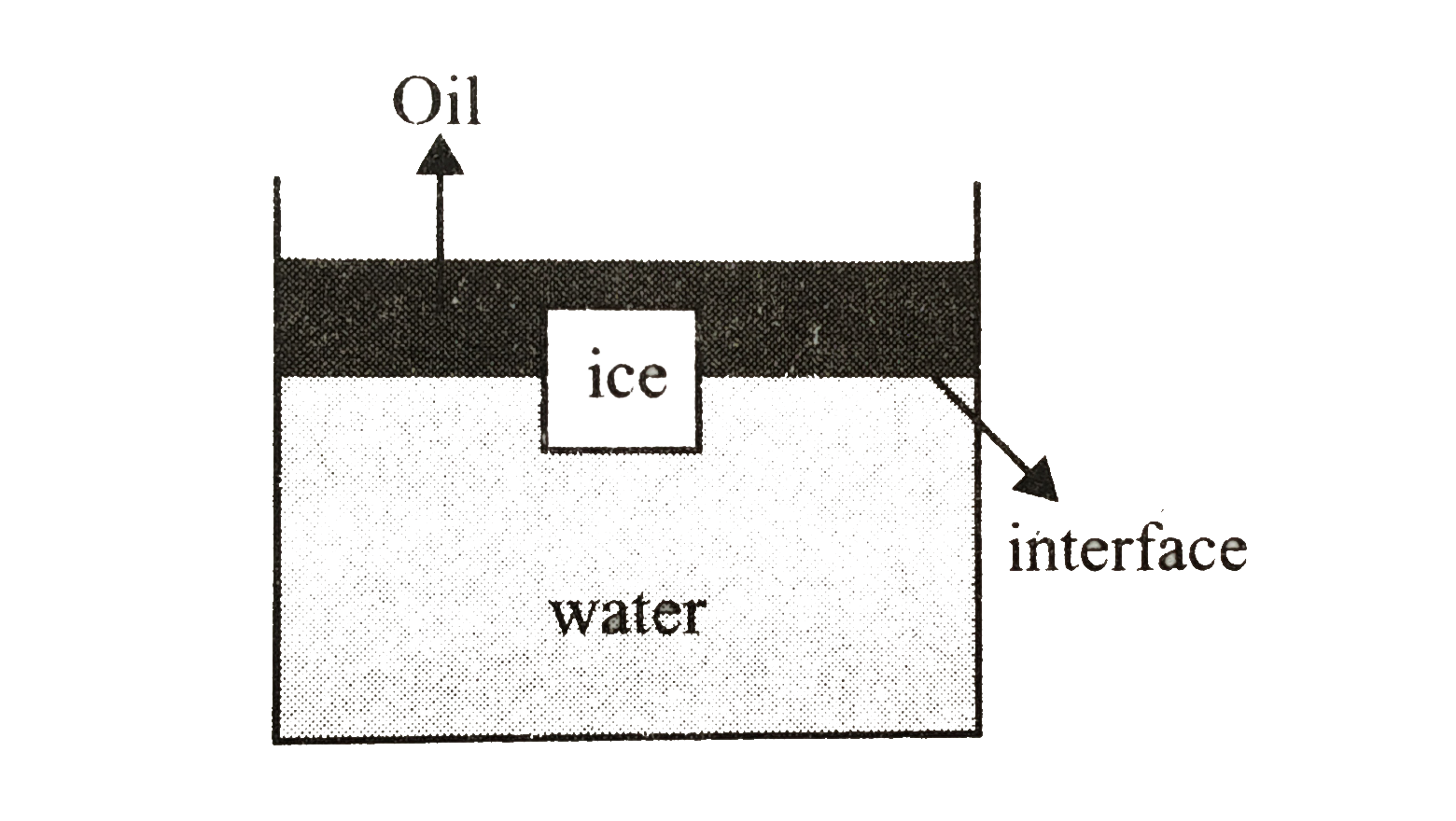
View SolutionA 700 g solid cube having an edge of length 10 cm floats in water. How much volume of the cube is outside the water? Density of water =1000kgm−3
View SolutionA metal piece weighing 15g is heated to 100∘C and then immersed in a mixture of ice and water at the thermal equilibrium. The volume of the mixture is found to be reduced by 0.15cm3 with the temperature of mixture remaining constant. Find the specific heat of the metal. Given specific gravity of ice =0.92, specific gravity of water at 0∘C=1.0, latent heat of fusion of ice =80cal−g−1.
View Solution