A metal piece weighing is heated to and then immersed in a mixture of ice and water at the thermal equilibrium. The volume of the mixture is found to be reduced by with the temperature of mixture remaining constant. Find the specific heat of the metal. Given specific gravity of ice , specific gravity of water at , latent heat of fusion of ice .
The correct Answer is:
To solve the problem, we will follow these steps:
Step 1: Understand the problem
We have a metal piece weighing 15 g that is heated to 100°C and then immersed in a mixture of ice and water. The volume of the mixture is reduced by 0.15 cm³, and we need to find the specific heat of the metal.
Step 2: Calculate the mass of ice melted
The reduction in volume of the mixture (0.15 cm³) indicates that some ice has melted. We can use the specific gravity of ice to find the mass of the ice that melted.
- Specific gravity of ice = 0.92
- Density of ice = 0.92 g/cm³
Using the formula for mass:
Mass of ice melted=Volume×Density=0.15cm3×0.92g/cm3=0.138g
Step 3: Calculate the heat lost by the ice
The heat lost by the ice as it melts can be calculated using the latent heat of fusion of ice.
- Latent heat of fusion of ice = 80 cal/g
Using the formula:
Qlost=m×L=0.138g×80cal/g=11.04cal
Step 4: Calculate the heat gained by the metal
The heat gained by the metal can be expressed as:
Qgained=mmetal×s×ΔT
Where:
- mmetal=15g
- ΔT=100−0=100°C (since the final temperature of the mixture is 0°C)
Thus,
Qgained=15g×s×100°C
Step 5: Set heat gained equal to heat lost
From the principle of calorimetry, we know that the heat gained by the metal is equal to the heat lost by the ice:
Qgained=Qlost
Substituting the values we have:
15g×s×100°C=11.04cal
Step 6: Solve for specific heat s
Rearranging the equation to solve for s:
s=11.04cal15g×100°C=11.041500≈0.00736cal/g°C
Step 7: Convert to appropriate units
To express the specific heat in a more standard form:
s≈0.00736cal/g°C≈0.0736cal/g°C
Final Answer
The specific heat of the metal is approximately 0.0736cal/g°C.
---
We have a metal piece weighing 15 g that is heated to 100°C and then immersed in a mixture of ice and water. The volume of the mixture is reduced by 0.15 cm³, and we need to find the specific heat of the metal.
The reduction in volume of the mixture (0.15 cm³) indicates that some ice has melted. We can use the specific gravity of ice to find the mass of the ice that melted.
- Density of ice = 0.92 g/cm³
Mass of ice melted=Volume×Density=0.15cm3×0.92g/cm3=0.138g
The heat lost by the ice as it melts can be calculated using the latent heat of fusion of ice.
Qlost=m×L=0.138g×80cal/g=11.04cal
The heat gained by the metal can be expressed as:
Qgained=mmetal×s×ΔT
Where:
- mmetal=15g
- ΔT=100−0=100°C (since the final temperature of the mixture is 0°C)
Qgained=15g×s×100°C
From the principle of calorimetry, we know that the heat gained by the metal is equal to the heat lost by the ice:
Qgained=Qlost
Substituting the values we have:
15g×s×100°C=11.04cal
Rearranging the equation to solve for s:
s=11.04cal15g×100°C=11.041500≈0.00736cal/g°C
To express the specific heat in a more standard form:
s≈0.00736cal/g°C≈0.0736cal/g°C
The specific heat of the metal is approximately 0.0736cal/g°C.
Topper's Solved these Questions
Similar Questions
Knowledge Check
The specific latent heat of fusion of water is :
A80 cal g−1B2260 J g−1C80 J g−1D336 J kg−1
2kg ice at −20∘C is mixed with 5kg water at 20∘C. Then final amount of water in the mixture will be: [specific heat of ice =0.5cal/gm∘C, Specific heat of water =1cal/gm∘C, Latent heat of fusion of ice =80cal/gm]
View Solution2kg ice at −20∘C is mixed with 5kg water at 20∘C. Then final amount of water in the mixture will be: [specific heat of ice =0.5cal/gm∘C, Specific heat of water =1cal/gm∘C, Latent heat of fusion of ice =80cal/gm]
View Solution1 g of ice at 0∘C is mixed with 1 g of steam at 100∘C. After thermal equilibrium is achieved, the temperature of the mixture is
View Solution19 g of water at 30∘C and 5 g of ice at −20∘C are mixed together in a calorimeter. What is the final temperature of the mixture? Given specific heat of ice =0.5calg−1(.∘C)−1 and latent heat of fusion of ice =80calg−1
View SolutionWhat will be the final temperature when 150 g of ice at 0∘C is mixed with 300 g of water at 50∘C. Specific heat of water =1cal/g/∘C. Latent heat of fusion of ice =80cal/g.
View SolutionTen litres of a liquid of specific gravity 1.3 is mixed with 6 litres of a liquid of specific gravity 0.8 the specific gravity of mixture is
View Solution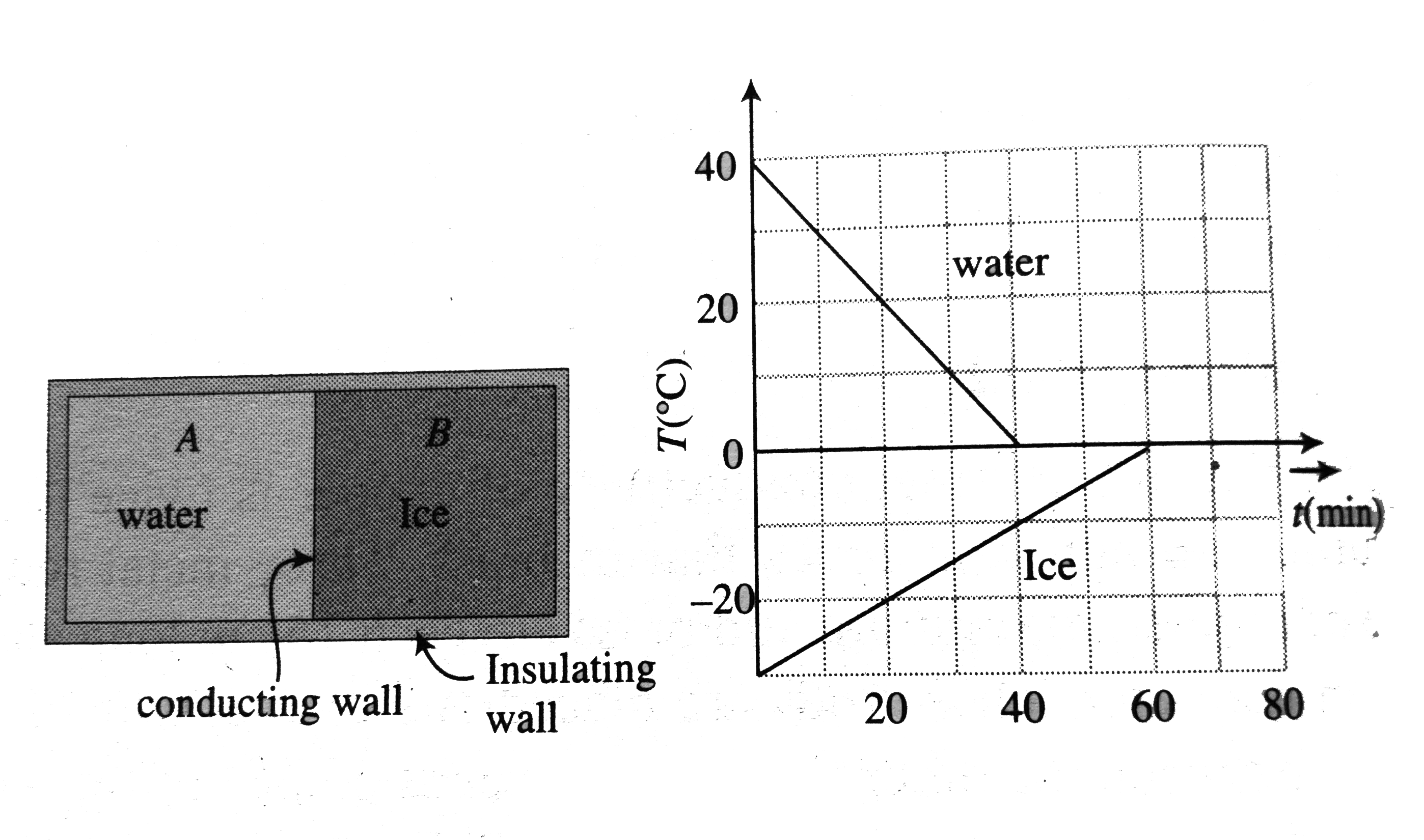
A 0.60 kg sample of water and a sample of ice are placed in two compartmetnts A and B separated by a conducting wall, in a thermally insulated container. The rate of heat transfer from the water to the ice through the conducting wall is constant P, until thermal equilibrium is reached. The temperature T of the liquid water and the ice are given in graph as functions of time t. Temperature of the compartments remain homogeneous during whole heat transfer process. Given specific heat of ice =2100J/kg−K, specific heat of water =4200J/kg−K, and latent heat of fusion of ice =3.3×105J/kg.
Initial mass of the ice in the container equal to
View Solution
