A block is kept on a rough horizontal plank. The coefficient of friction between the block and the plank is . The plank is undergoing SHM of angular frequency 10 rad/s. The maximum amplitude of plank in which the block does not slip over the plank is (g= 10 m/)
4cm
5cm
10cm
16cm
The correct Answer is:B
, or
Topper's Solved these Questions
- SIMPLE HARMONIC MOTION BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - LEVEL (2)
40 Videos
- SIMPLE HARMONIC MOTION BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - 6-previous year question
56 Videos
- SIMPLE HARMONIC MOTION BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - LEVEL 0 LONG ANSWER TYPE
2 Videos
- ROTATIONAL MOTION BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - JEE Advanced (Archive) (True/False Type)
3 Videos
- SYSTEM OF A PARTICLES & ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF A PARTICLES & ROTATIONAL MOTIONEXERCISE - IN-CHAPTER EXERCISE F
10 Videos
Similar Questions
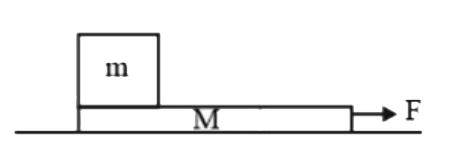
A bolck of mass m =2 kg is placed on a plank of mass M = 10 kg, which is placed on a smooth horizontal plane as shown in the figure. The coefficient of friction between the block and the plank is μ=13. If a horizontal force F is applied on the plank, then the maximum value of F for which the block and the plank move together is (g=10m/s2)
View SolutionA block of mass m=2kg of shown dimensions is placed on a plank of mass M = 6Kg which is placed on smooth horizontal plane. The coefficient of friction between the block and the plank is μ=13. If a horizontal froce F is applied on the plank, then find the maximum value of F (in N) for which the block and the plank move together

View SolutionA block is kept on a horizontal table. The table is undergoing simple farmonic motion of frequency 3Hz in a horizontal plane. The coefficient of static friction between the block and the table surface is 0.72. find the maximum amplitude of the table at which the block does not slip on the surface g=10ms−1
View SolutionA block is placed over a plank. The coefficient of friction between the block and the plank is μ=0.2. Initially both are at rest, suddenly the plank starts moving with acceleration a0=4m/s2. The displacement of the block in 1 is (g=10m/s2)
View SolutionA block of mass m is gently placed over a massive plank moving horizontal over a smooth surface with velocity 10ms−1. The coefficient of friction between the block and the plank is 0.2. The distance travelled by the block till it slides on the plank is [g=10ms−2]
View SolutionA block of mass M=4kg of height and breath b is placed on a rough plank of same mass M. A light inextensible string is connected to the upper end of the block and passed through a light smooth pulley as shown in figure. A mass m=1kg is hung to the other end of the string.
a. What should be the minimum value of coefficient of friction between the block and the plank so that, there is no slipping between the block and the wedge?
b. Find the minimum value of b/h so that the block does not topple over the plank, friction is absent between the plank and the ground.

View SolutionA block of mass 2 kg slides down an incline plane of inclination 30°. The coefficient of friction between block and plane is 0.5. The contact force between block and plank is :
View SolutionA block of mass m kept on rough horizontal turn table at a distance x from the centre. If the coefficient of friction between the table and block is μ then maximum speed of point P on turn table so that the block does not slip is

View SolutionA small block of mass 1kg is placed over a plank of mass 2kg. The length of the plank is 2 m. coefficient of friction between the block and the plnak is 0.5 and the ground over which plank in placed is smooth. A constant force F=30N is applied on the plank in horizontal direction. the time after which the block will separte from the plank is (g=10m/s2)
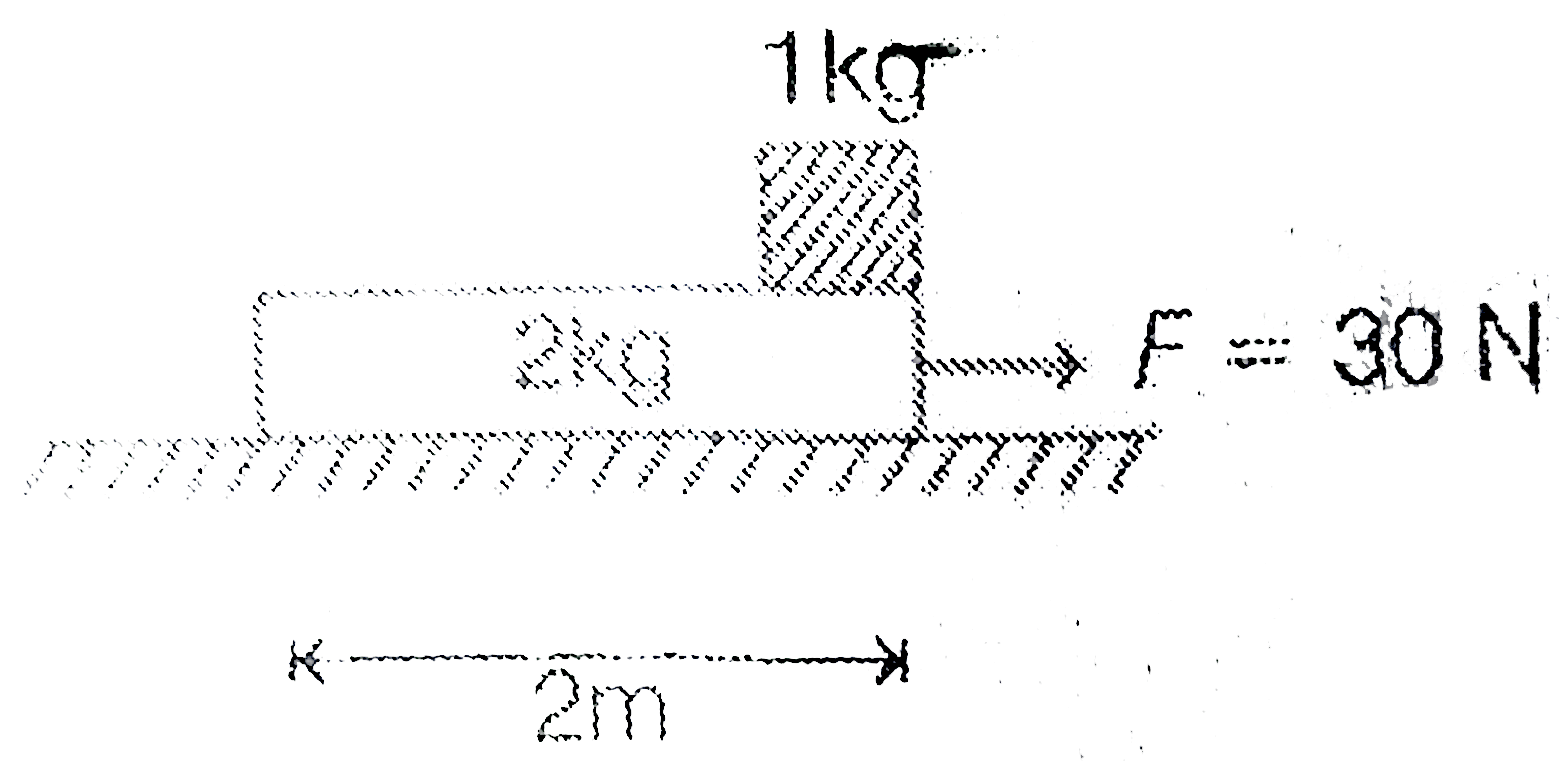
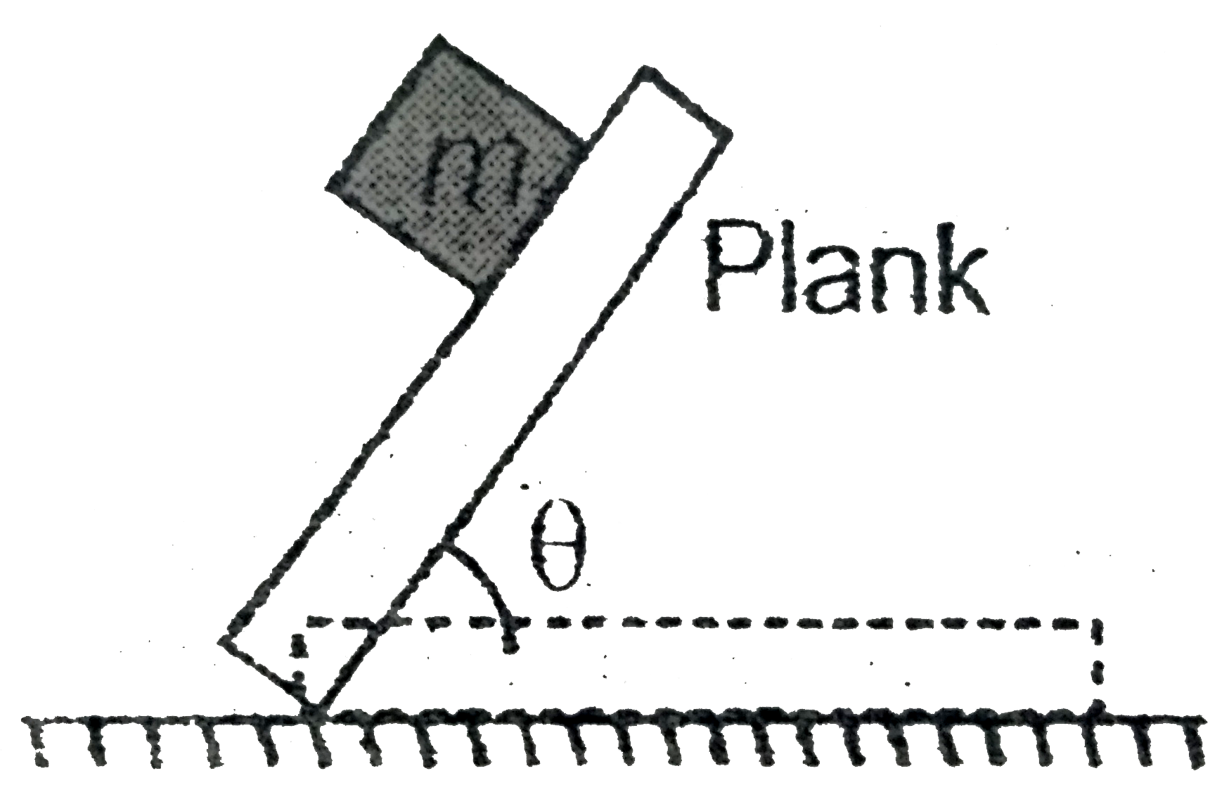
View SolutionA block of mass m is kept on a plank . The coefficient of friction between the plank and block is 1. The plank is slowly raised from one end so that it makes angle θ with horizontal . The forces of friction acting on the plank , when θ=30∘andθ60∘ are respectively,
View Solution
