A plank with a bar placed on it performs horizontal harmonic oscillations with amplitude a=10cm. Find the coefficient of friction between the bar and the plank if the former starts sliding along the plank when the amplitude of oscillation of the plank becomes less than T=1.0s.
The correct Answer is:0.4
To solve the problem, we need to find the coefficient of friction (μ) between the bar and the plank, given that the bar starts sliding when the amplitude of oscillation of the plank becomes less than T = 1.0 s.
1. Understanding the Problem:
- The bar is placed on a plank that performs horizontal harmonic oscillations with an amplitude a=10cm=0.1m.
- The bar will start sliding when the maximum acceleration of the plank exceeds the maximum static friction force acting on the bar.
2. Maximum Acceleration in SHM:
- The maximum acceleration amax in Simple Harmonic Motion (SHM) is given by the formula:
amax=aω2
- Where a is the amplitude and ω is the angular frequency.
3. Finding Angular Frequency (ω):
- The angular frequency ω is related to the time period T by the formula:
ω=2πT
- Given T=1.0s:
ω=2π1=2πrad/s
4. Calculating Maximum Acceleration:
- Substitute a=0.1m and ω=2π:
amax=0.1×(2π)2
- Calculate (2π)2:
(2π)2=4π2
- Therefore:
amax=0.1×4π2
5. Friction Force:
- The maximum static friction force Fs is given by:
Fs=μmg
- Where m is the mass of the bar and g is the acceleration due to gravity (approximately 10m/s2).
6. Setting Up the Equation:
- For the bar to start sliding, the maximum static friction must equal the maximum acceleration force:
μmg=mamax
- Canceling m from both sides gives:
μg=amax
7. Substituting Values:
- Substitute g=10m/s2 and amax=0.1×4π2:
μ×10=0.1×4π2
- Rearranging gives:
μ=0.1×4π210
- Simplifying:
μ=0.01×4π2
8. Approximating π²:
- Using π2≈10:
μ=0.01×4×10=0.4
Final Answer:
The coefficient of friction μ between the bar and the plank is 0.4.
- The bar is placed on a plank that performs horizontal harmonic oscillations with an amplitude a=10cm=0.1m.
- The bar will start sliding when the maximum acceleration of the plank exceeds the maximum static friction force acting on the bar.
- The maximum acceleration amax in Simple Harmonic Motion (SHM) is given by the formula:
amax=aω2
- Where a is the amplitude and ω is the angular frequency.
- The angular frequency ω is related to the time period T by the formula:
ω=2πT
- Given T=1.0s:
ω=2π1=2πrad/s
- Substitute a=0.1m and ω=2π:
amax=0.1×(2π)2
- Calculate (2π)2:
(2π)2=4π2
- Therefore:
amax=0.1×4π2
- The maximum static friction force Fs is given by:
Fs=μmg
- Where m is the mass of the bar and g is the acceleration due to gravity (approximately 10m/s2).
- For the bar to start sliding, the maximum static friction must equal the maximum acceleration force:
μmg=mamax
- Canceling m from both sides gives:
μg=amax
- Substitute g=10m/s2 and amax=0.1×4π2:
μ×10=0.1×4π2
- Rearranging gives:
μ=0.1×4π210
- Simplifying:
μ=0.01×4π2
- Using π2≈10:
μ=0.01×4×10=0.4
The coefficient of friction μ between the bar and the plank is 0.4.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTION BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - LEVEL (2)
40 Videos
- SIMPLE HARMONIC MOTION BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - 6-previous year question
56 Videos
- SIMPLE HARMONIC MOTION BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - LEVEL 0 LONG ANSWER TYPE
2 Videos
- ROTATIONAL MOTION BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - JEE Advanced (Archive) (True/False Type)
3 Videos
- SYSTEM OF A PARTICLES & ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF A PARTICLES & ROTATIONAL MOTIONEXERCISE - IN-CHAPTER EXERCISE F
10 Videos
Similar Questions
A bolck of mass m =2 kg is placed on a plank of mass M = 10 kg, which is placed on a smooth horizontal plane as shown in the figure. The coefficient of friction between the block and the plank is μ=13. If a horizontal force F is applied on the plank, then the maximum value of F for which the block and the plank move together is (g=10m/s2)
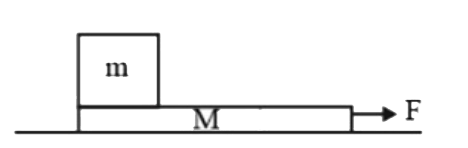
View SolutionA block of mass m=2kg of shown dimensions is placed on a plank of mass M = 6Kg which is placed on smooth horizontal plane. The coefficient of friction between the block and the plank is μ=13. If a horizontal froce F is applied on the plank, then find the maximum value of F (in N) for which the block and the plank move together

View SolutionA block is kept on a rough horizontal plank. The coefficient of friction between the block and the plank is 12. The plank is undergoing SHM of angular frequency 10 rad/s. The maximum amplitude of plank in which the block does not slip over the plank is (g= 10 m/s2)
View SolutionA block of mass m is gently placed over a massive plank moving horizontal over a smooth surface with velocity 10ms−1. The coefficient of friction between the block and the plank is 0.2. The distance travelled by the block till it slides on the plank is [g=10ms−2]
View SolutionA horizontal plane supports a plank with a bar of mass m placed on it and attached by a light elastic non-deformed cord of length l0, to a point O. The coefficient of friciton between the bar and the plank is equal to m. The plank is slowly shifted to the right until the bar starts sliding over it. It occurs at the moment when the cord derivates from the vertical by an angle θ.
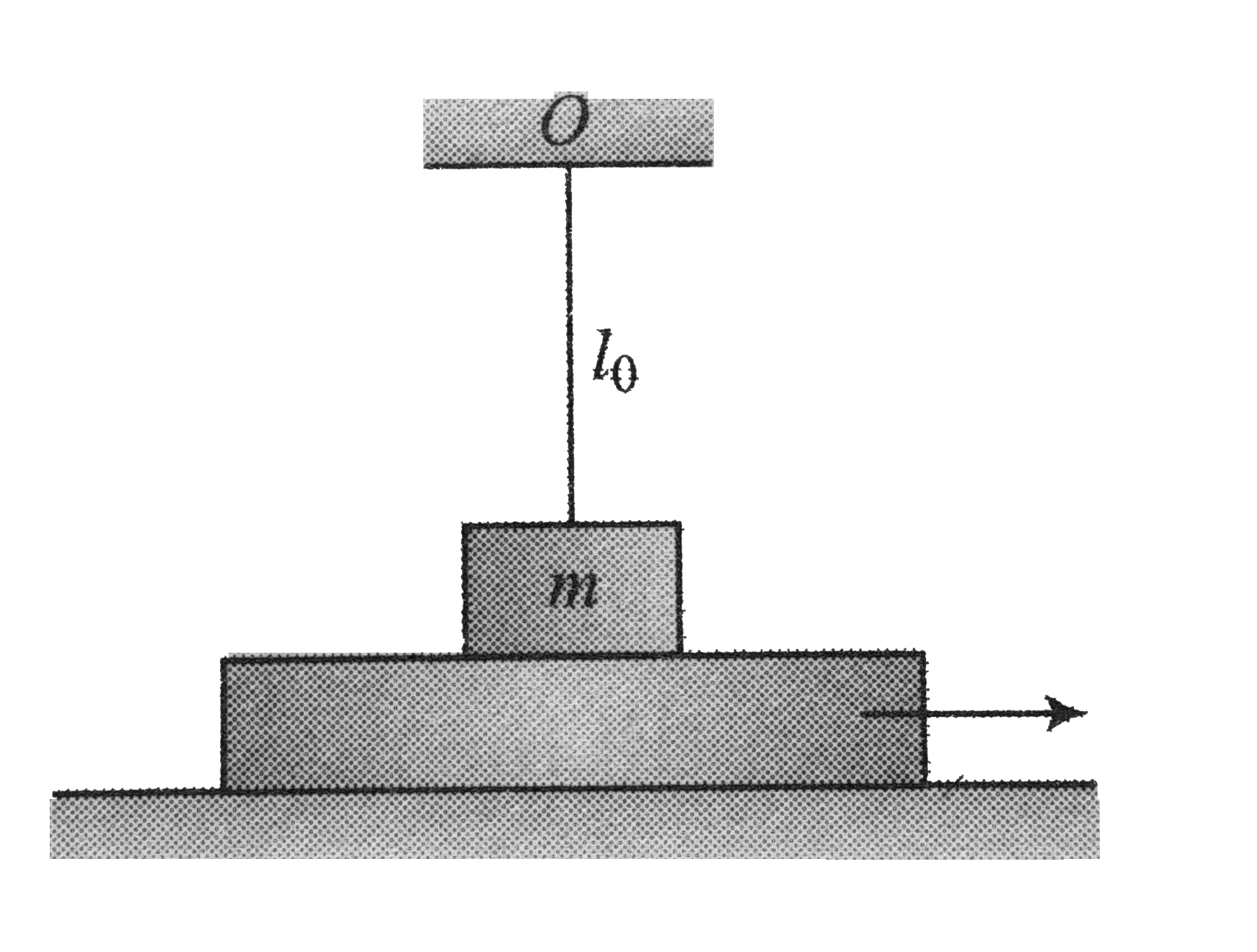
Find the work that has been performed by the moment by the frictional force acting on the bar in the reference frame fixed to the plane.
View SolutionBlock A of mass m rests on the plank B of mass 3m which is free to slide on a frictionless horizo-ntal surface. The coefficient of friction between the block and plank is 0.2. If a horizontal force of magnitude 2 mg is applied to the plank B, the acceleration of A relative to the plank and relative to the ground respectively, are:

View SolutionA particle executes a simple harmonic motion of amplitude 1.0 cm along the principal axis of a convex lens of focal length 12 cm. The mean position of oscillation is at 20 cm from the lens. Find the amplitude of oscillation of the image of the particle.
View SolutionIn the figure shown, a solid sphere of mass 'm' and radius r is released from a height 6r to slide down a smooth surface. A plank of same mass 'm' touches the horizontal portion of the surface at the ground. The co-efficient of friction between the plank and the sphere is μ and that between the plank and the ground is μ/4. Find the work done by the friction force between the plank and the ground till the sphere starts pure rolling on the plank. Neglect the height of the plank.

View SolutionA long horizontal plank of mass m is lying on a smooth horizontal surface. A sphere of same mass m and radius r is spinned about its own axis with angular velocity we and gently placed on the plank. The coefficient of friction between the plank and the sphere is μ. After some time the pure rolling of the sphere on the plank will start. Answer the following questions.

Find the displacement of the plank till the sphere starts pure rolling.
View SolutionA plank of mass 2kg and length 1m is placed on horizontal floor.A small block of mass 1kg is placed on top of the plank , at its right extreme end .The coefficient of friction between plank and floor is 0.5 and that between plank and block is 0.2 . If a horizontal force =30N starts acting on the plank to the right ,the time after which the block will fall off the plank is (g=10ms−2)
View Solution

