A mass hangs in equilibrium from a spring of constant K=2N/cmAnother mass of 3 kg is placed over M. Find the new amplitude of oscillation after wards (in m) (Takeg=10m/s−2)
The correct Answer is:0.15
To solve the problem step by step, we will follow the principles of equilibrium and simple harmonic motion (SHM).
Step 1: Understand the Problem
We have a spring with a spring constant K=2N/cm and a mass m hanging from it. When an additional mass of 3kg is placed on top of m, we need to find the new amplitude of oscillation.
Step 2: Convert Units
First, we need to convert the spring constant from N/cm to N/m:
K=2N/cm=2×100N/m=200N/m
Step 3: Set Up the Equations
1. When the mass m is hanging in equilibrium, the force due to gravity is balanced by the spring force:
mg=Kx1
where x1 is the initial displacement of the spring.
2. When the additional mass 3kg is added, the new equilibrium condition is:
(m+3)g=Kx2
where x2 is the new displacement of the spring.
Step 4: Subtract the Equations
To find the change in displacement due to the added mass, we subtract the first equation from the second:
(m+3)g−mg=Kx2−Kx1
This simplifies to:
3g=K(x2−x1)
Step 5: Solve for the Change in Displacement
Rearranging gives:
x2−x1=3gK
Step 6: Substitute Values
Now, substitute g=10m/s2 and K=200N/m:
x2−x1=3×10200
x2−x1=30200=0.15m
Step 7: Conclusion
The new amplitude of oscillation after adding the mass is:
Amplitude=0.15m
Final Answer
The new amplitude of oscillation is 0.15m.
---
We have a spring with a spring constant K=2N/cm and a mass m hanging from it. When an additional mass of 3kg is placed on top of m, we need to find the new amplitude of oscillation.
First, we need to convert the spring constant from N/cm to N/m:
K=2N/cm=2×100N/m=200N/m
1. When the mass m is hanging in equilibrium, the force due to gravity is balanced by the spring force:
mg=Kx1
where x1 is the initial displacement of the spring.
(m+3)g=Kx2
where x2 is the new displacement of the spring.
To find the change in displacement due to the added mass, we subtract the first equation from the second:
(m+3)g−mg=Kx2−Kx1
This simplifies to:
3g=K(x2−x1)
Rearranging gives:
x2−x1=3gK
Now, substitute g=10m/s2 and K=200N/m:
x2−x1=3×10200
x2−x1=30200=0.15m
The new amplitude of oscillation after adding the mass is:
Amplitude=0.15m
The new amplitude of oscillation is 0.15m.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTION BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - LEVEL (2)
40 Videos
- SIMPLE HARMONIC MOTION BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - 6-previous year question
56 Videos
- SIMPLE HARMONIC MOTION BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - LEVEL 0 LONG ANSWER TYPE
2 Videos
- ROTATIONAL MOTION BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - JEE Advanced (Archive) (True/False Type)
3 Videos
- SYSTEM OF A PARTICLES & ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF A PARTICLES & ROTATIONAL MOTIONEXERCISE - IN-CHAPTER EXERCISE F
10 Videos
Similar Questions
A block of mass m hangs from three springs having same spring constant k. If the mass is slightly displaced downwards, the time period of oscillation will be

View SolutionA block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View Solution
Knowledge Check
Natural length of a spring is 60 cm and its spring constant is 4000 N/m. A mass of 20 kg is hung from it. The extension produced in the spring is (Take, g=9.8m/s2)
A4.9 cmB0.49 cmC9.4 cmD0.94 cm
Block of mass m2 is in equilibrium as shown in figure. Anotherblock of mass m1 is kept gently on m2. Find the time period of oscillation and amplitude.
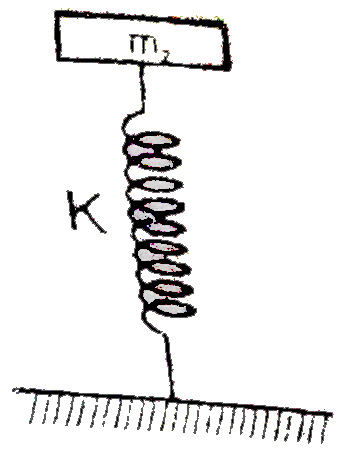
View SolutionBlock of mass m2 is in equilibrium as shown in figure. Anotherblock of mass m1 is kept gently on m2. Find the time period of oscillation and amplitude.
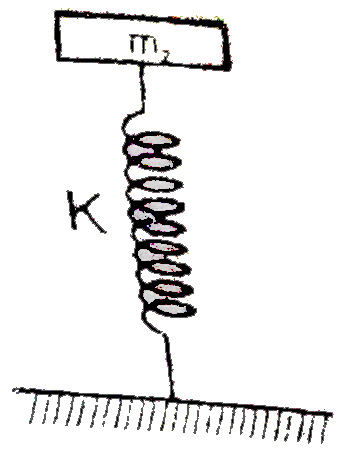
View SolutionA cage of mass M hangs from a light spring of force constant k. A body of mass m falls from height h inside the cage and stricks to its floor. The amplitude of oscillations of the cage will be-
_E01_061_Q01.png)
View SolutionThe system is in equilibrium and at rest. Now mass m1 is removed from m2. Find the time period and amplituded of resultant motion. Spring constant is K.

View SolutionA block of mass m suspended from a spring of spring constant k. Find the amplitude of S.H.M.
View SolutionA mass m = 8kg is attached to a spring as shown in figure and held in positioin so that the spring remains unstretched. The spring constant is 200 N/m. The mass m is then released and begins to undergo small oscillations. The maximum velocity of the mass will be (g=10m/s2)
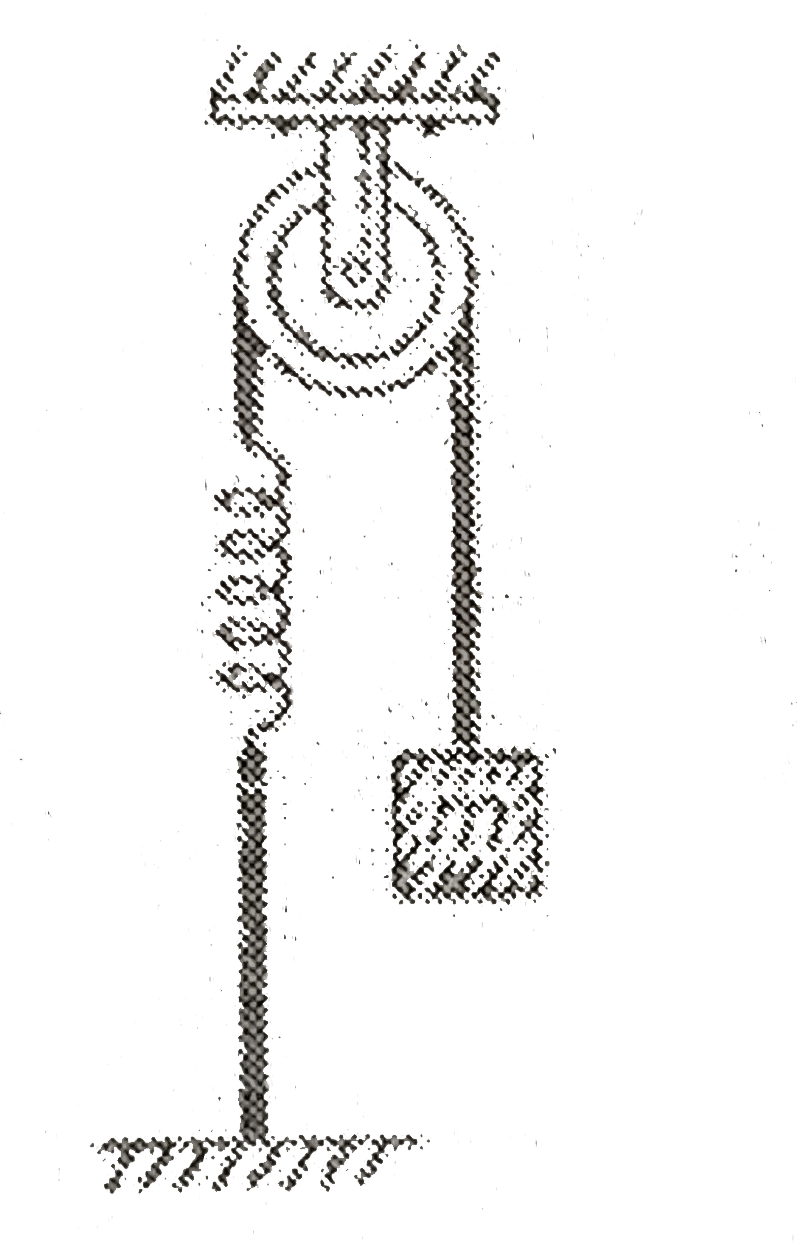
View SolutionA mass of 2.0kgis put on a that pan attached to a vertical spring fixed on the ground as shown in the figure The mass of the spring and the pen is negligible the mass executing a simple harmonic motion The spring constant is 200N/m what should be the minimum amplitude of the motion so that the mass get detached from the pan? (Tak∈gg=10m/s2)

View Solution
