Infinite springs with force constants k,2k, 4k and 8k … respectively are connected in series. What will be the effective force constant of springs, when
The correct Answer is:1
To solve the problem of finding the effective force constant of an infinite series of springs with force constants k,2k,4k,8k,…, we will follow these steps:
1. Identify the Force Constants: The force constants of the springs are k,2k,4k,8k,…. We can express these in terms of k:
- k1=k
- k2=2k
- k3=4k
- k4=8k
- And so on...
2. Use the Formula for Springs in Series: When springs are connected in series, the effective force constant kequiv is given by the formula:
1kequiv=1k1+1k2+1k3+…
3. Substitute the Force Constants: Substitute the values of the force constants into the formula:
1kequiv=1k+12k+14k+18k+…
4. Factor Out 1k: We can factor out 1k from the right-hand side:
1kequiv=1k(1+12+14+18+…)
5. Recognize the Infinite Geometric Series: The series 1+12+14+18+… is an infinite geometric series where:
- The first term a=1
- The common ratio r=12
6. Calculate the Sum of the Infinite Series: The sum S of an infinite geometric series is given by:
S=a1−r
Substituting the values:
S=11−12=112=2
7. Substitute Back to Find kequiv: Now substitute the sum back into the equation for 1kequiv:
1kequiv=1k⋅2
Therefore:
kequiv=k2
8. Substitute the Value of k: Given k=10N/m:
kequiv=102=5N/m
Final Answer:
The effective force constant of the infinite springs connected in series is 5N/m.
- k1=k
- k2=2k
- k3=4k
- k4=8k
- And so on...
1kequiv=1k1+1k2+1k3+…
1kequiv=1k+12k+14k+18k+…
1kequiv=1k(1+12+14+18+…)
- The first term a=1
- The common ratio r=12
S=a1−r
Substituting the values:
S=11−12=112=2
1kequiv=1k⋅2
Therefore:
kequiv=k2
kequiv=102=5N/m
The effective force constant of the infinite springs connected in series is 5N/m.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTION Book:VMC MODULES ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:LEVEL (2)
Explore 40 Videos
- SIMPLE HARMONIC MOTION Book:VMC MODULES ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:6-previous year question
Explore 56 Videos
- SIMPLE HARMONIC MOTION Book:VMC MODULES ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:LEVEL 0 LONG ANSWER TYPE
Explore 2 Videos
- ROTATIONAL MOTION Book:VMC MODULES ENGLISHChapter:ROTATIONAL MOTION Exercise:JEE Advanced (Archive) (True/False Type)
Explore 3 Videos
- SYSTEM OF A PARTICLES & ROTATIONAL MOTIONBook:VMC MODULES ENGLISHChapter:SYSTEM OF A PARTICLES & ROTATIONAL MOTIONExercise:IN-CHAPTER EXERCISE F
Explore 10 Videos
Similar Questions
Infinite springs with force constantk , 2k, 4k and 8 k .... respectively are connected in series. The effective force constant of the spring will b
View SolutionForce constant of a spring (k) is anonymous to
View SolutionTwo springs of spring constantsK1 and K2 are joined in series. The effective spring constant of the combination is given by
View SolutionTwo springs of spring constantsK1 and K2 are joined in series. The effective spring constant of the combination is given by
View SolutionAs shown in the figure, two light springs of force constant k1 and k2 oscillate a block of mass m. Its effective force constant will be

View SolutionFour massless springs whose force constants are 2k, 2k, k and 2k respectively are attached to a mass M kept on a frictionless plane (as shown in figure). If the mass M is displaced in the horizontal direction.

View SolutionTwo spring P and Q having stiffness constants k1 and k2(<k1), respectively are stretched equally. Then
View SolutionA spring of force constant k. is cut into lengths of ratio 1:2:3. They are connected in series and the new force constant is k'. Then they are connected in parallel and force constant is k''. Then K':K'' is
View SolutionA spring of force constant k is cut into lengths of ratio 1:2:3. They are connected in series and the new force constant is k'. Then they are connected in parallel and force constant is k'. Then k' : k" is :
View SolutionA block of mass m is attached to three springs A,B and C having force constants k,k and 2k respectively as shown in figure. If the block is slightly oushed against spring C. If the angular frequency of oscillations is √Nkm, then find N. The system is placed on horizontal smooth surface.
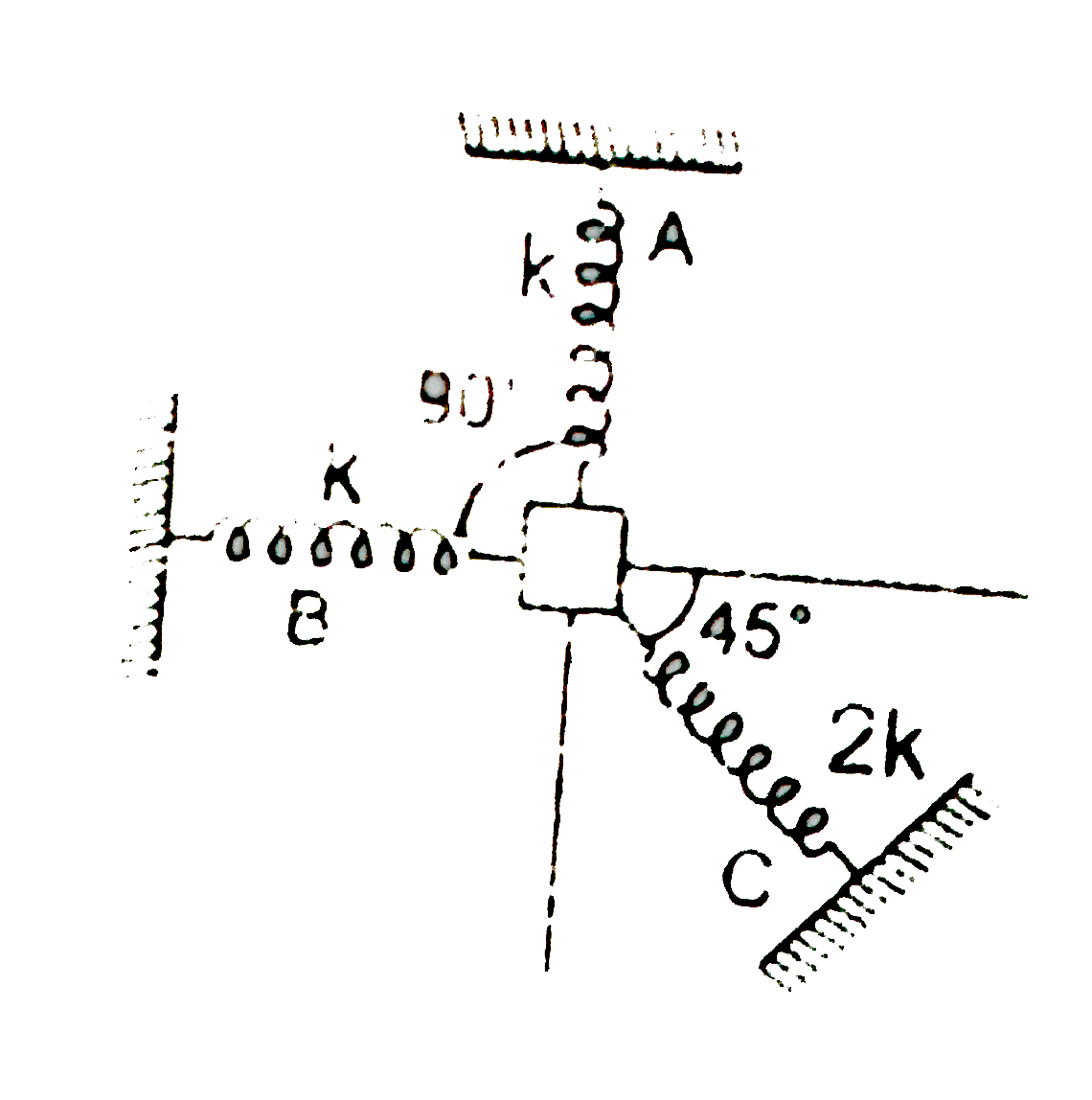
View Solution
