The disk has a weight of 100Nand rolls without slipping on the horizontal surface as it oscillates about its equilibrium position. If the disk is displaced, by rolling it counterclockwise 0.4rad, determine the equation which describes its oscillatory motion when it is released.
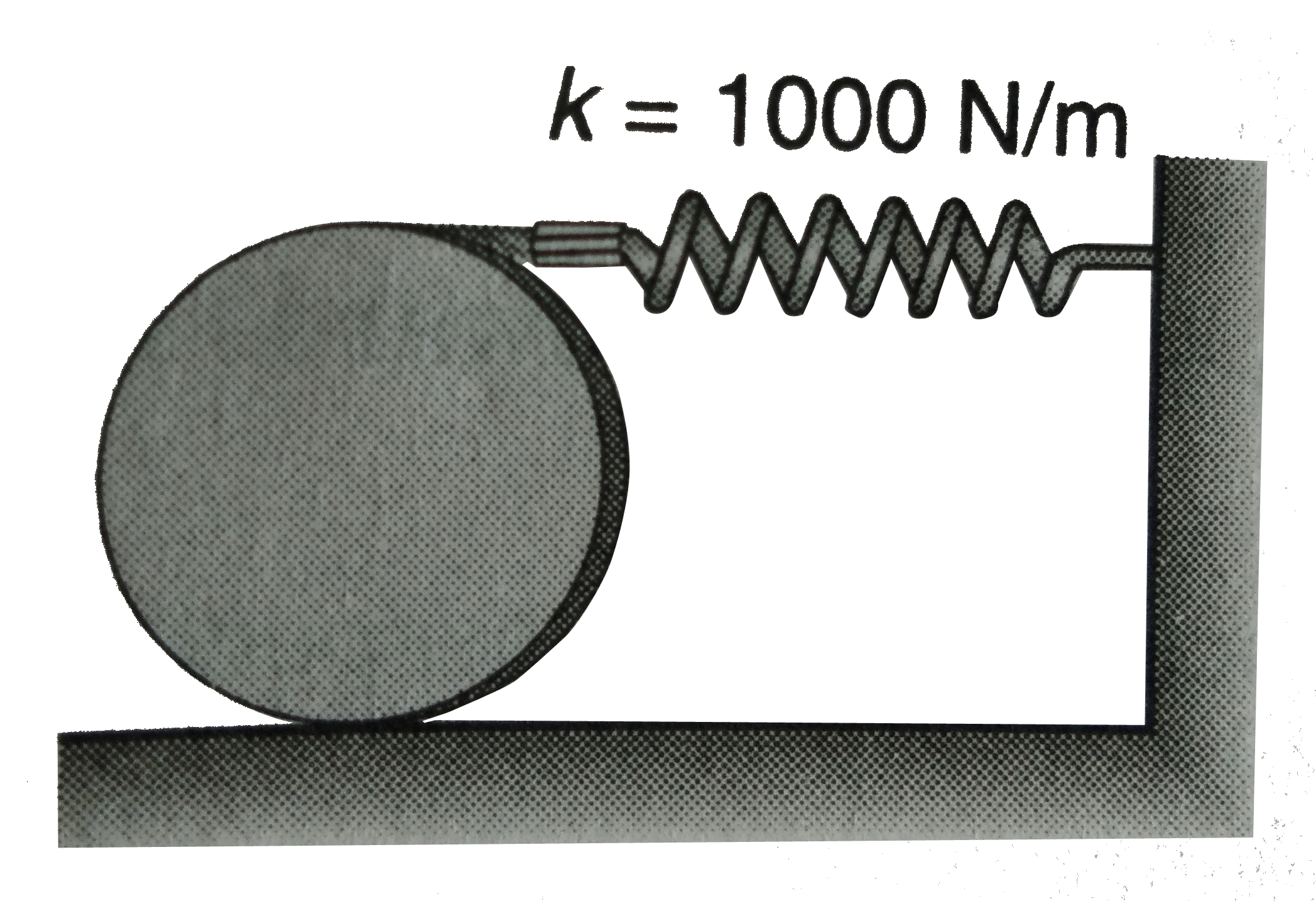
The correct Answer is:A, C, D
In the displaced position,
E=12mv2+12Iω2+12k(2x)2
I=12mR2 and ω=vR
∴E=34mv2+2kx2
E= constant
∴dEdt=0
or 32mvdvdt+4kxdxdt=0
Substituting, dxdt=v and dvdt=a
a=−8k3m.x
Comparing with, a=−ω2x
We have
ω=√8k3m=√8×10003×1009.8=16.16rad/s
∴θ=θ0cosωt
or θ=0.4cos(16.16t).
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBook:DC PANDEY ENGLISHChapter:SIMPLE HARMONIC MOTIONExercise:Exercise 14.1
Explore 5 Videos
- SIMPLE HARMONIC MOTIONBook:DC PANDEY ENGLISHChapter:SIMPLE HARMONIC MOTIONExercise:Intro. Exer.
Explore 1 Video
- SIMPLE HARMONIC MOTIONBook:DC PANDEY ENGLISHChapter:SIMPLE HARMONIC MOTIONExercise:Level 2 Comprehension
Explore 2 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBook:DC PANDEY ENGLISHChapter:SEMICONDUCTORS AND ELECTRONIC DEVICESExercise:More than One Option is Correct
Explore 3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBook:DC PANDEY ENGLISHChapter:SOLVD PAPERS 2017 NEET, AIIMS & JIPMERExercise:Solved paper 2018(JIPMER)
Explore 38 Videos
Similar Questions
A ring rolls without slipping on a horizontal surface. At any instant its position is as shown in the figure.
View Solution
A uniform circular ring rolls without slipping on a horizontal surface. At any instant, its position is as shown in the figure. Then
View SolutionA solid cylinder of mass M and radius R rolls without slipping on a flat horizontal surface. Its moment of inertia about the line of contact is
View SolutionA 4 kg roller is attached to a massless spring of spring constant k = 100 N/m. It rolls without slipping along a frcitionless horizontal road. The roller is displaced from its equilibrium position by 10 cm and then released. It rolls without slipping along a frictionless horizontal road. The roller is displaced from its equilibrium position by 10 cm and then released. Its maximum speed will be
View SolutionA uniform disc of mass m and radius r rolls without slipping along a horizontal surface and ramp, as shown above. The disk has an initial velocity of υ . What is the maximum height h to which the center of mass of the disc rises ?

View SolutionA disc of radius 20CM is rolling without slipping on a flat horizontal surface. At a certain instant the velocity of its centre is 4m/s and its angular velocity is 10rad/s. The lowest contact point is O.
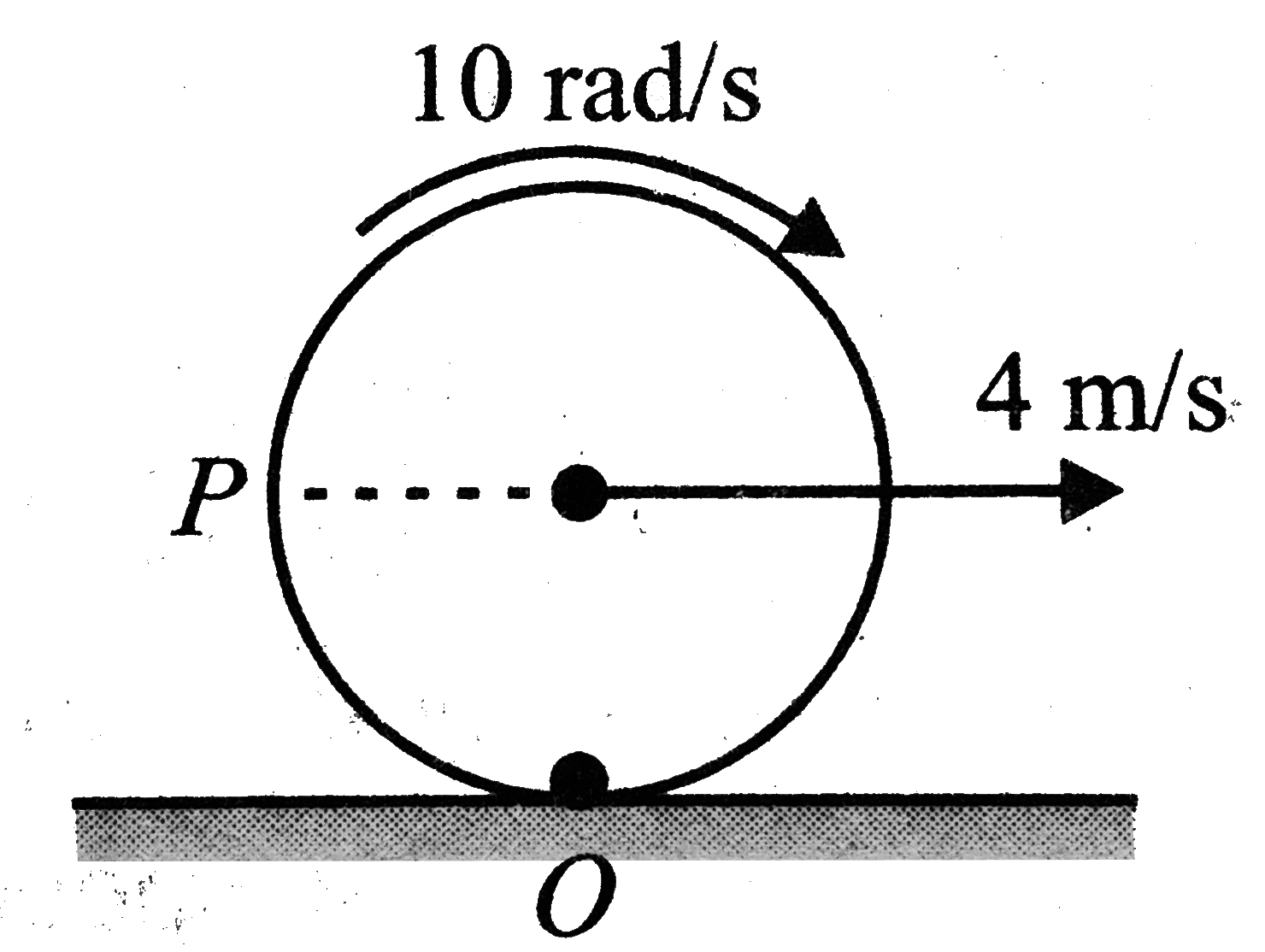
Velocity of point P is
View SolutionA 5kg collar is attached to a spring . It slides without friction over a horizontal surface. It is displaced from its equilibrium position by 10 cm and released , its maximum speed is 1ms−1 Calculate
(a) Spring constant
(b) The period of oscillation
(c ) Maximum acceleration of the collar
Hint :m=5kg,A=0.1m,k=?,T=?or a=?,vm=1ms−1
vm=Aω=A√km
Find k,
T=2π√mk
amax=ω2A=kmA
View SolutionA disc of radius 20CM is rolling with slipping on a flat horizontal surface. At a certain instant the velocity of its centre is 4m/s and its angular velocity is 10rad/s. The lowest contact point is O.
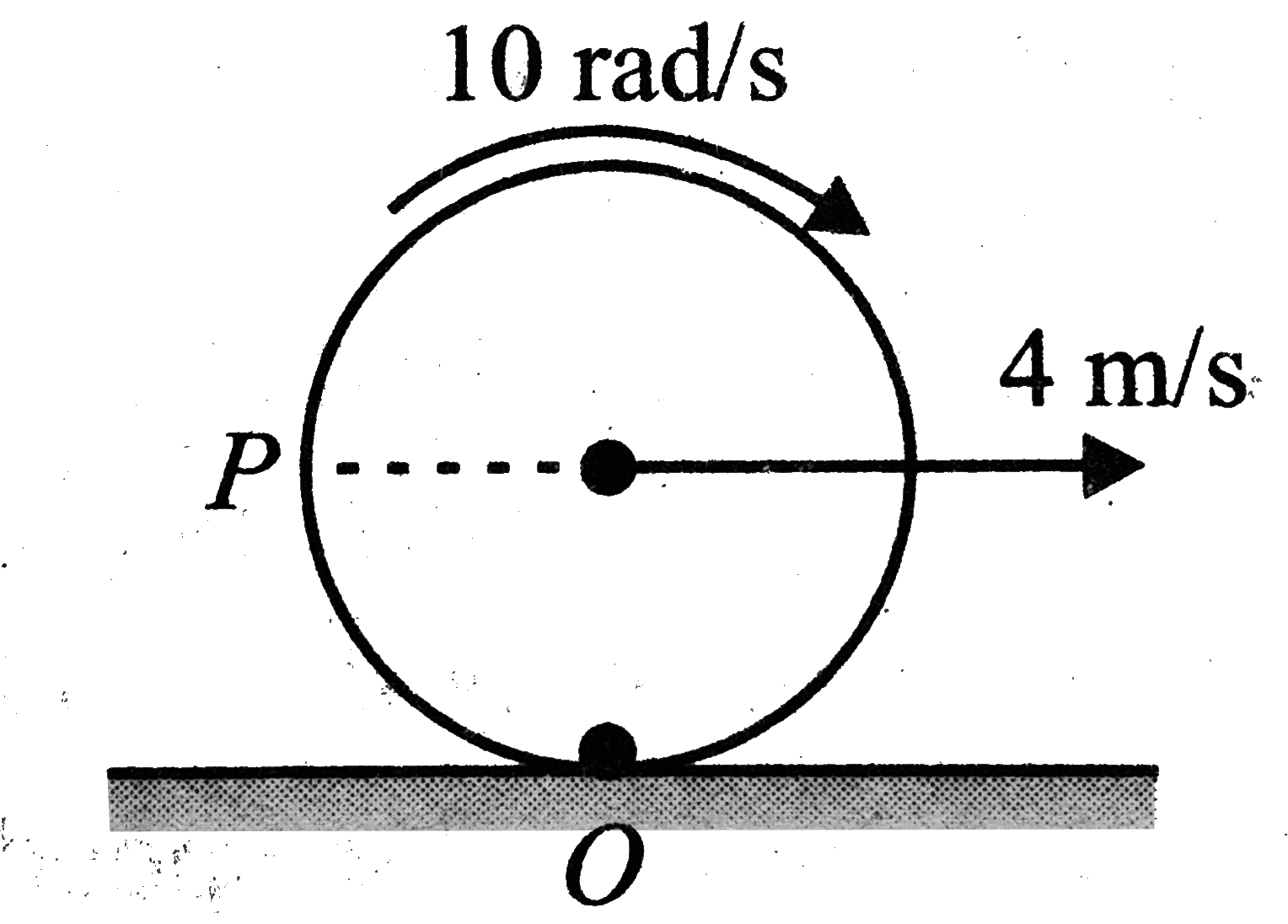
Velocity of point O is
View SolutionA 2.5 kg collar attached to a spring of foce constant 1000 Nm−1 slides without friction on a horizontal rod. The collar is displaced from its equilibrium position by 5.0 cm and released. Calculate (i) the period of oscillation (ii) the maximum speed of the collar and (iii) the maximum acceleration of the collar.
View SolutionThe wheel of radius R rolls wihtout slipping on horizontal rough surface and its centre O has an acceleration a0 in forward direction. A point P on the wheel is a distance r from O and angular position θ from horizontal. Find the angle θ for which point P can have zero acceleration in this position .

View Solution
