A 2.5 kg collar attached to a spring of foce constant 1000 Nm−1 slides without friction on a horizontal rod. The collar is displaced from its equilibrium position by 5.0 cm and released. Calculate (i) the period of oscillation (ii) the maximum speed of the collar and (iii) the maximum acceleration of the collar.
To solve the problem step by step, we will calculate the period of oscillation, the maximum speed of the collar, and the maximum acceleration of the collar.
Given Data:
- Mass of the collar, m=2.5kg
- Spring constant, k=1000N/m
- Displacement from equilibrium (amplitude), A=5cm=0.05m
(i) Calculate the Period of Oscillation
The formula for the period T of a spring-mass system is given by:
T=2π√mk
Substituting the values:
T=2π√2.51000
Calculating the fraction:
2.51000=0.0025
Now, taking the square root:
√0.0025=0.05
Now substituting back into the equation for T:
T=2π×0.05=2π20=π10s
(ii) Calculate the Maximum Speed of the Collar
The maximum speed Vmax in simple harmonic motion is given by:
Vmax=Aω
Where ω (angular frequency) is given by:
ω=√km
Calculating ω:
ω=√10002.5=√400=20rad/s
Now substituting A and ω into the equation for Vmax:
Vmax=0.05×20=1m/s
(iii) Calculate the Maximum Acceleration of the Collar
The maximum acceleration Amax in simple harmonic motion is given by:
Amax=Aω2
Substituting the values we have:
Amax=0.05×(20)2
Calculating (20)2:
(20)2=400
Now substituting back:
Amax=0.05×400=20m/s2
Summary of Results:
1. Period of oscillation, T=π10s
2. Maximum speed of the collar, Vmax=1m/s
3. Maximum acceleration of the collar, Amax=20m/s2
- Mass of the collar, m=2.5kg
- Spring constant, k=1000N/m
- Displacement from equilibrium (amplitude), A=5cm=0.05m
1. Period of oscillation, T=π10s
2. Maximum speed of the collar, Vmax=1m/s
3. Maximum acceleration of the collar, Amax=20m/s2
Similar Questions
A 5 kg collar is attached to a spring of spring constant 500Nm−1 . It slides without friction over a horizontal rod. The collar is displaced from its equilibrium position by 10 cm and released. Calculate (a) The period of oscillations (b) The maximum speed and (c) maximum acceleration of the collar.
View SolutionA 2.5 kg collar is attached to a spring of spring constant 250Nm−1 . It slides without friction over a horizontal surface . It is displaced from its equilibrium position by 20 cm and releasd. Calculate the period of osciallation and the maximum speed.
View Solution
Knowledge Check
A 5 kg collar is attached to a spring of spring constant 500 N m−1. It slides without friction over a horizontal rod. The collar is displaced from its equilibrium position by 10 cm and released. The time period of oscillation is
Aπ5sBπ2sCπsD2πs
A 10 kg collar is attached to a spring of spring constant 1000Nm−1 . It slides without friction over a horizontal surface. If is displaced from its equilibrium position by 20 cm and released . Calculate
(a) The period of oscillation (b) The maximum speed
Hint :T=2π√mk,vm=Aω=A√km
View SolutionA 5kg collar is attached to a spring . It slides without friction over a horizontal surface. It is displaced from its equilibrium position by 10 cm and released , its maximum speed is 1ms−1 Calculate
(a) Spring constant
(b) The period of oscillation
(c ) Maximum acceleration of the collar
Hint :m=5kg,A=0.1m,k=?,T=?or a=?,vm=1ms−1
vm=Aω=A√km
Find k,
T=2π√mk
amax=ω2A=kmA
View SolutionA trolley of mass 3.0kg is connected to two identical spring each of force constant 600Nm−1 as shown in figure. If the trolley is displaced from its equilibrium position by 5.0 cm and released, what is
(a) the period of ensuing oscillation?
(b) the maximum speed of trolley?
(c) How much is the total energy dissipated as heat by the time the trolley comes to rest due to damping forces?

View SolutionA mass of 1.5 kg is connected to two identical springs each of force constant 300Nm−1 as shown in the figure. If the mass is displaced from its equilibrium position by 10cm, then the period of oscillation is

View SolutionA mass of 1.5 kg is connected to two identical springs each of force constant 300Nm−1 as shown in the figure. If the mass is displaced from its equilibrium position by 10 cm, then maximum speed of the trolley is
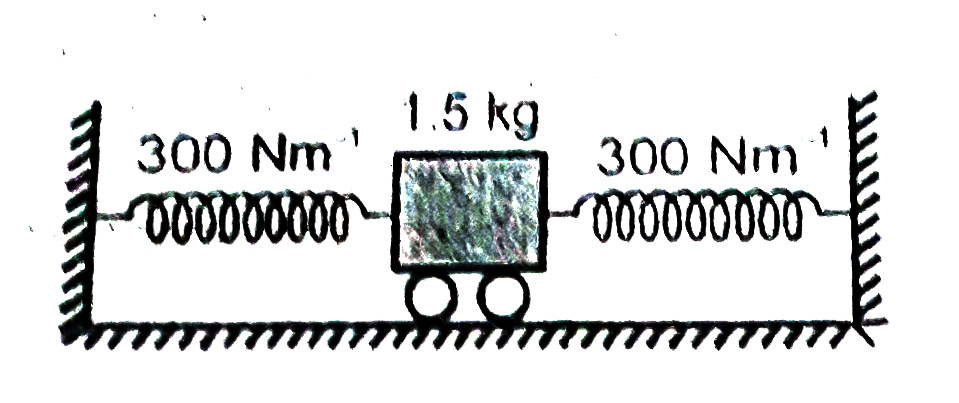
View SolutionA 4 kg roller is attached to a massless spring of spring constant k = 100 N/m. It rolls without slipping along a frcitionless horizontal road. The roller is displaced from its equilibrium position by 10 cm and then released. It rolls without slipping along a frictionless horizontal road. The roller is displaced from its equilibrium position by 10 cm and then released. Its maximum speed will be
View SolutionA 10 kg metal block is attached to a spring constant 1000Nm−1. A block is displaced from equilibrium position by 10 cm and released. The maximum acceleration of the block is
View Solution
