Find the time period of the oscillation of mass m in figure a,b,c what is the equivalent spring constant of the pair oif springs in each case?
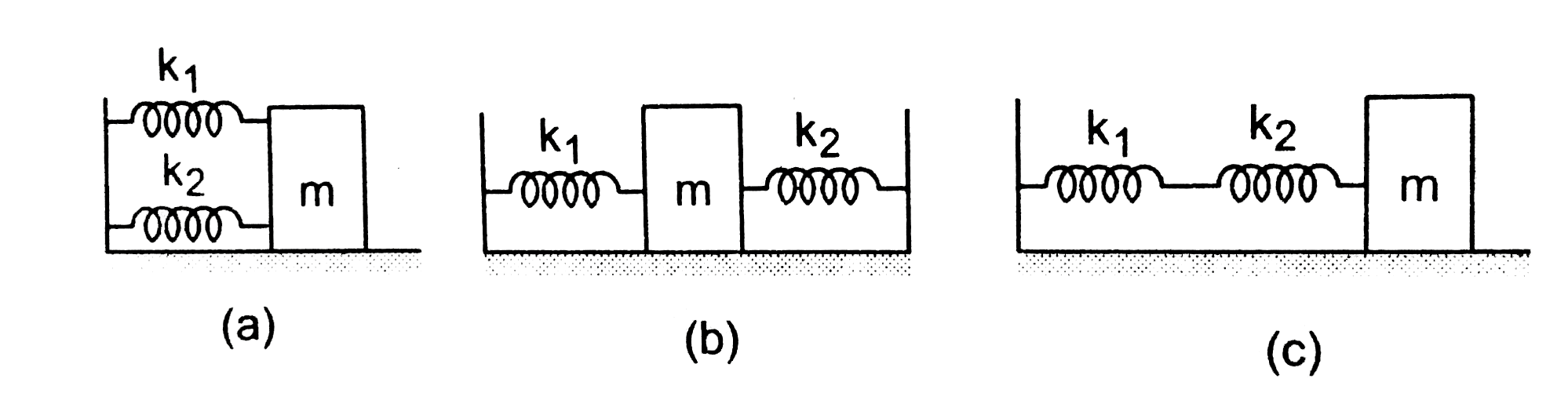
The correct Answer is:=2π√mk1+k2
=2π(√m(k1+k2)k1k2)
a. Equivalent spring constant
=k=k1+k2(parallel)
T=2π√mk=2π√mk1+k2
b. Let us displace theh block m towards left through dislacement x.
Resultant force F=F1+F2=(k1+k2)
Acceleration
(Fm)=(k1+k2)mx
Timeperiod
=T=2π√displacementAe≤ration
→2π√xx(k1+k2m)
=2π√mk1+k2
The equivalent spring constant
k=k1+k2 . c In series connectionn equivalent spring constant be k
So,k 1k=1k1+1k2=k2+k1k1k2
→K=k1k2k1+k2
T=2√mk
=2π(√m(k1+k2)k1k2)
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBook:HC VERMA ENGLISHChapter:SIMPLE HARMONIC MOTIONExercise:Question for short Answer
Explore 15 Videos
- SIMPLE HARMONIC MOTIONBook:HC VERMA ENGLISHChapter:SIMPLE HARMONIC MOTIONExercise:Objective-2
Explore 15 Videos
- ROTATIONAL MECHANICSBook:HC VERMA ENGLISHChapter:ROTATIONAL MECHANICSExercise:Questions for short Answer
Explore 21 Videos
- SOME MECHANICAL PROPERTIES OF MATTERBook:HC VERMA ENGLISHChapter:SOME MECHANICAL PROPERTIES OF MATTERExercise:Objective-2
Explore 7 Videos
Similar Questions
Knowledge Check
What is the mechanical equivalent of spring constant k in LC oscillating circuit?
A1LB1CCLCD1LCIf the period of oscillation of mass M suspended. From a spring is one second, then the period of 4 M will be
A1/2B1/4 secC2 secD4 sec
The pulley shown in figure has a moment of inertias I about its axis and mass m. find the time period of vertical oscillation of its centre of mass. The spring has spring constant k and the string does not slip over the pulley.

View SolutionIf the period of oscillation of mass M suspended from a spring is one second, then the period of 9M will be
View SolutionDerive an experession for the period of oscillation of a mass attached to a spring executing simple harmonic motion. Given that the period of oscillation depends on the mass m and the force constant k, where k is the force required to stretch the spring by unit length?
View SolutionFigure a) shows a spring of force constant k clamped rigidly at once end and a mass m attached to its free end. A force F applied at the free end stretches the spring. Figure b) shows the same spring with both ends free and attached to a mass m at either end. Each end of the spring in figure is stretched by the same force F.
(a) What is the maximum extension of the spring in the two cases ?
(b) If the mass in figure and the two masses in figure are released free, what is the period of oscillation in each case?

View SolutionFigure a) shows a spring of force constant k clamped rigidly at once end and a mass m attached to its free end. A force F applied at the free end stretches the spring. Figure b) shows the same spring with both ends free and attached to a mass m at either end. Each end of the spring in figure is stretched by the same force F.
(a) What is the maximum extension of the spring in the two cases ?
(b) If the mass in figure and the two masses in figure are released free, what is the period of oscillation in each case?

View SolutionSpring constant of a spring is calculated using formule K=4π2MT2, where T is time period of vertical oscillation when mass M is hung with the help of spring to rigid support. If time of oscillation for 10 oscillations is measured to be 5.0 s and mass M=0.20 kg, find possible error in spring constant K.
View Solution