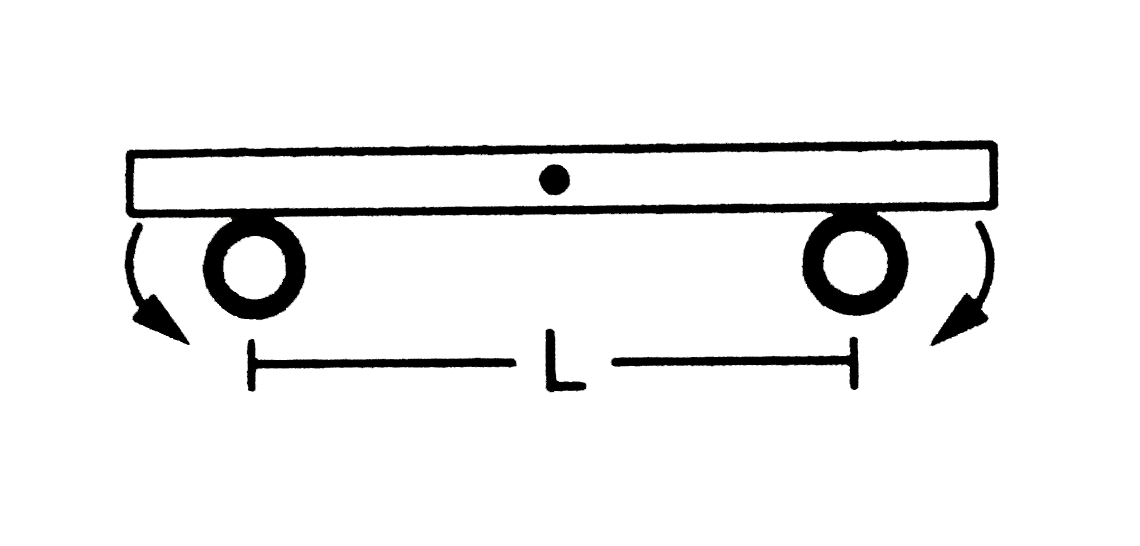
A uniform table of mas M stays horizontally and symmetrically on two wheels rotatig in opposite directions figure. The separsation between the wheels is L. The friction coefficeint between each whee, and the plate is μ. Find the time period of oscilationof the pate if it is slightly displaced along its length and released.
The correct Answer is:B
Let x be the displacement of the plank towards left. Now the centre of gravity is also displaced through x.
R1+R2=mg
Taking moment about g we get
R1(l2−x)=R2(12−x)
=(mg−R1)(l2+x)…………1ltbr>gt S,R1(l2−x)=(mg−R1)(l2+x)
→R112−R1x=
mgl2−R1x+mgx−R1l2
L →R−1l2+R1l2=mg(x+12)
→R1(l2+l2)=mg(2x+12)
→R1l=mg(2x+1)<br>R1=mg(1+2x2l .........i
Now, F1=μR1=μmg((1+2x))2l
similarly F2=μR=μmg((1+2x))2l
similarlty F2=μR2=μMg((1+2x))2l
sin F1>F2
→F1−F2=ma−(2μmgl)x
ax=2μ=mgl=ω2
→=ωμ√gl
:Timeperiod=2pisqrt(l/(2mug))
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Question for short Answer
15 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Objective-2
15 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for short Answer
21 Videos
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMA ENGLISHCHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Objective-2
7 Videos
Similar Questions
Two wheels which are rotated by some external source with constant angular velocity in opposite directions as shown in figure. A uniform plank of mass M is placed on it symmetrically. The friction co-efficient between each wheel and the plank is μ. find the frequency of oscillations, when plank is slightly displaced along its length and released.

View SolutionA uniform chain of length L and mass M overhangs a horizontal table with its two third part n the table. The friction coefficient between the table and the chain is μ. Find the work done by the friction during the period the chain slips off the table.
View SolutionA uniform chain of length L and mass M overhangs a horizontal table with its two third part n the table. The friction coefficient between the table and the chain is μ. Find the work done by the friction during the period the chain slips off the table.
View SolutionA uniform horizontal plank is resting symmetrically in a horizontal position on two cylindrical droms , which are apinning in in opposite direction about their horizontal axes with equal angular velocity . The distance between the axes with equal angular velocity. The distance between the axes is 2L and the coefficient of friction between the plank and cylender is μ . If the plank is displaced slightly from the equilibrium position along its length and released, show that it performs simple horizontal motion. Caculate also the time period of motion.
View SolutionA uniform chain of length L and mass M overhangs a horizontal table with its two third part on the table. The friction coefficient between the table and the chain is µ. The work done by the friction during the period the chain slips off the table is [−2kμMgL]. Find the value of k.
View SolutionA block of mass M is pulled along a horizontal surface by applying a force at angle θ with the horizontal. The friction coefficient between the block and the surface is μ. If the block travels at a uniform velocity, find the work done by this applied force during a displacement d of the block.
View SolutionA block of mass M is pulled along a horizontal surface by applying a force at angle θ with the horizontal. The friction coefficient between the block and the surfasce is μ. If the block travels at a uniform velocity, find the work donen by this applied force during a displacement d of the blcok.
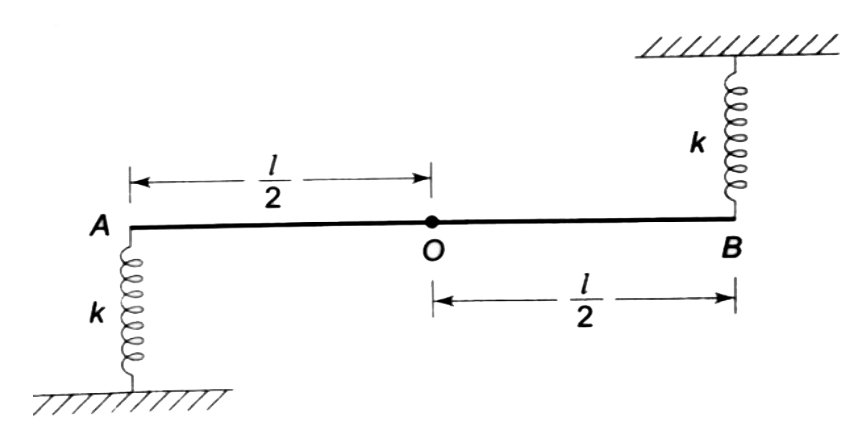
View SolutionThe ends of a rod of length l and mass m are attached to two identical springs as shown in the figure. The rod is free to rotate about its centre O . The rod is depressed slightly at end A and released . The time period of the oscillation is
View SolutionFigure shown a small block A of mass m kept at the left end of a plank B of mass M=2m and length l . The system can slide on a horizontal road. The system is started towards right with the initial velocity v. The friction coefficient between the road and the plank is 1/2 and that between the plank and the block is 1/4 . Find

(a) the time elapsed before the block separates from the plank
(b) displacement of block and plank relative to ground till that moment.
View SolutionTwo particles, each having a mass of 5 g and charge. 1.0×10−7 C, stay in limiting quilibrium on a horizontal. table with a separation of 10 cm between them. The coefficient of friction between each partcle and the table. is the same. Find the value of this coefficient.
View Solution
