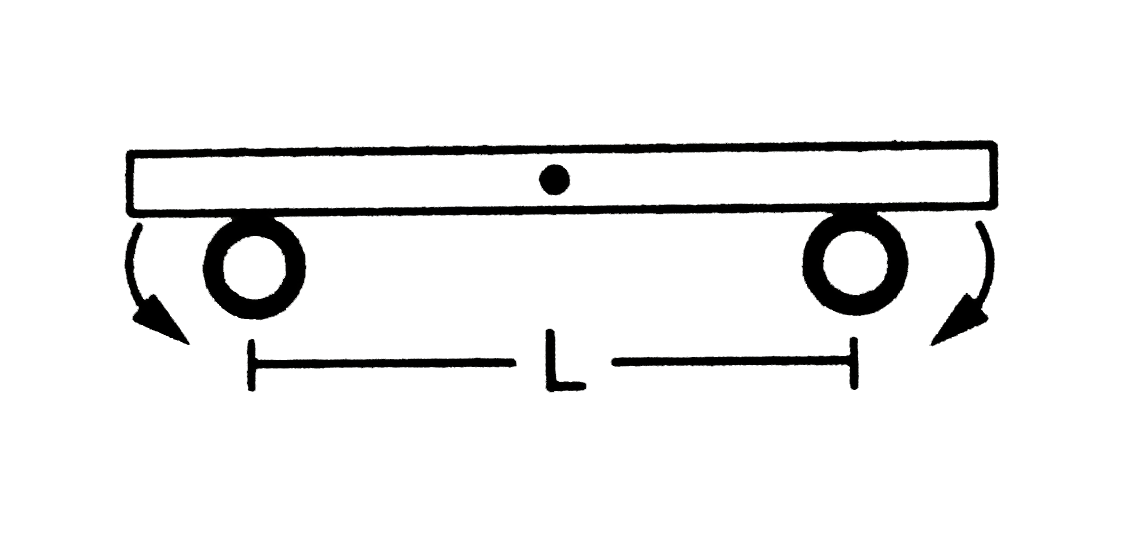
A uniform horizontal plank is resting symmetrically in a horizontal position on two cylindrical droms , which are apinning in in opposite direction about their horizontal axes with equal angular velocity . The distance between the axes with equal angular velocity. The distance between the axes is 2L and the coefficient of friction between the plank and cylender is μ . If the plank is displaced slightly from the equilibrium position along its length and released, show that it performs simple horizontal motion. Caculate also the time period of motion.
To solve the problem step by step, we will analyze the situation of the plank resting on two cylindrical drums and derive the equations governing its motion.
Step 1: Understand the Setup
- We have a uniform horizontal plank resting symmetrically on two cylindrical drums.
- The distance between the axes of the drums is 2L.
- The drums are rotating in opposite directions with equal angular velocity.
- The coefficient of friction between the plank and the cylinders is μ.
Step 2: Analyze the Forces
- When the plank is in equilibrium, the normal forces from the drums (RA and RB) and the weight of the plank (mg) balance each other.
- If the plank is displaced slightly by a distance x from the equilibrium position, the normal forces will change due to the shift in the center of mass.
Step 3: Determine the Normal Forces
- Let RA be the normal force from the left drum and RB be the normal force from the right drum.
- From the equilibrium condition:
RA+RB=mg(1)
- When the plank is displaced by x, the distances from the center of mass to the drums become L+x and L−x respectively.
Step 4: Write the Torque Equations
- The torque about the center of mass due to the normal forces can be expressed as:
RA⋅(L+x)=RB⋅(L−x)(2)
Step 5: Solve the Equations
- From equations (1) and (2), we can express RA and RB in terms of mg and x.
- Substitute RB=mg−RA into equation (2):
RA⋅(L+x)=(mg−RA)⋅(L−x)
- Rearranging gives:
RA(L+x)+RA(L−x)=mg(L−x)
- Simplifying leads to:
2LRA=mg(L−x)
- Thus, we find:
RA=mg(L−x)2LandRB=mg(L+x)2L
Step 6: Calculate the Restoring Force
- The frictional force F acting on the plank due to the normal forces is:
F=μRA−μRB
- Substituting the expressions for RA and RB:
F=μ(mg(L−x)2L)−μ(mg(L+x)2L)
- This simplifies to:
F=−μmgLx
- This is a restoring force proportional to the displacement x, indicating simple harmonic motion.
Step 7: Identify the Motion Type
- Since the restoring force can be expressed as:
F=−kxwhere k=μmgL
- The motion is simple harmonic motion (SHM).
Step 8: Calculate the Time Period
- The time period T of SHM is given by:
T=2π√mk
- Substituting k:
T=2π√mμmgL=2π√Lμg
Final Result
- The plank performs simple harmonic motion, and the time period of the motion is:
T=2π√Lμg
- We have a uniform horizontal plank resting symmetrically on two cylindrical drums.
- The distance between the axes of the drums is 2L.
- The drums are rotating in opposite directions with equal angular velocity.
- The coefficient of friction between the plank and the cylinders is μ.
- When the plank is in equilibrium, the normal forces from the drums (RA and RB) and the weight of the plank (mg) balance each other.
- If the plank is displaced slightly by a distance x from the equilibrium position, the normal forces will change due to the shift in the center of mass.
- Let RA be the normal force from the left drum and RB be the normal force from the right drum.
- From the equilibrium condition:
RA+RB=mg(1)
- When the plank is displaced by x, the distances from the center of mass to the drums become L+x and L−x respectively.
- The torque about the center of mass due to the normal forces can be expressed as:
RA⋅(L+x)=RB⋅(L−x)(2)
- From equations (1) and (2), we can express RA and RB in terms of mg and x.
- Substitute RB=mg−RA into equation (2):
RA⋅(L+x)=(mg−RA)⋅(L−x)
- Rearranging gives:
RA(L+x)+RA(L−x)=mg(L−x)
- Simplifying leads to:
2LRA=mg(L−x)
- Thus, we find:
RA=mg(L−x)2LandRB=mg(L+x)2L
- The frictional force F acting on the plank due to the normal forces is:
F=μRA−μRB
- Substituting the expressions for RA and RB:
F=μ(mg(L−x)2L)−μ(mg(L+x)2L)
- This simplifies to:
F=−μmgLx
- This is a restoring force proportional to the displacement x, indicating simple harmonic motion.
- Since the restoring force can be expressed as:
F=−kxwhere k=μmgL
- The motion is simple harmonic motion (SHM).
- The time period T of SHM is given by:
T=2π√mk
- Substituting k:
T=2π√mμmgL=2π√Lμg
- The plank performs simple harmonic motion, and the time period of the motion is:
T=2π√Lμg
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Exercise 4.1
23 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Exercise 4.2
23 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Single correct anwer type
14 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
Similar Questions
A skater of mass m standing on ice throws a stone of mass M with a velocity of v in a horizontal direction. The distance over which the skater will move back (the coefficient of friction between the skater and the ice is μ)
View SolutionThe friction coefficient between plank and floor is μ. The man applies, the maximum possible force on the string and the system remains at rest. Then

View SolutionA cylinder rests on a horizontal rotating disc, as shown in the figure. Find at what angular velocity, ω, the cylinder falls off the disc, if the distance between the axes of the disc and cylinder is R, and the coefficient of friction μ>D/h where D is the diameter of the cylinder and It is its height.

View SolutionA uniform table of mas M stays horizontally and symmetrically on two wheels rotatig in opposite directions figure. The separsation between the wheels is L. The friction coefficeint between each whee, and the plate is μ. Find the time period of oscilationof the pate if it is slightly displaced along its length and released.
View SolutionA ring of radius R is first rotated with an angular velocity ω and then carefully placed on a rough horizontal surface. The coefficient of friction between the surface and the ring is μ. Time after which its angular speed is reduced to half is
View SolutionA long horizontal plank of mass m is lying on a smooth horizontal surface. A sphere of same mass m and radius r is spinned about its own axis with angular velocity we and gently placed on the plank. The coefficient of friction between the plank and the sphere is μ. After some time the pure rolling of the sphere on the plank will start. Answer the following questions.

Find the displacement of the plank till the sphere starts pure rolling.
View SolutionA long horizontal plank of mass m is lying on a smooth horizontal surface. A sphere of same mass m and radius r is spinned about its own axis with angular velocity we and gently placed on the plank. The coefficient of friction between the plank and the sphere is μ. After some time the pure rolling of the sphere on the plank will start. Answer the following questions.
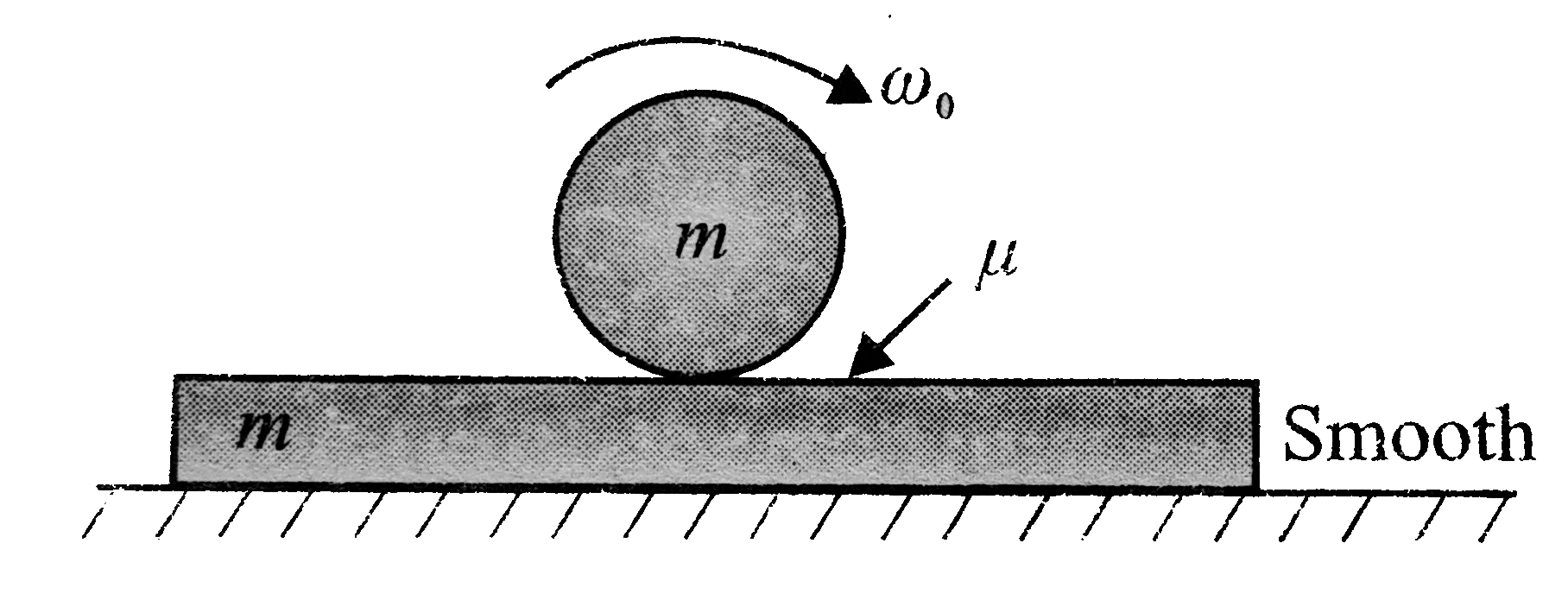
Find the time t at which the pure roiling starts
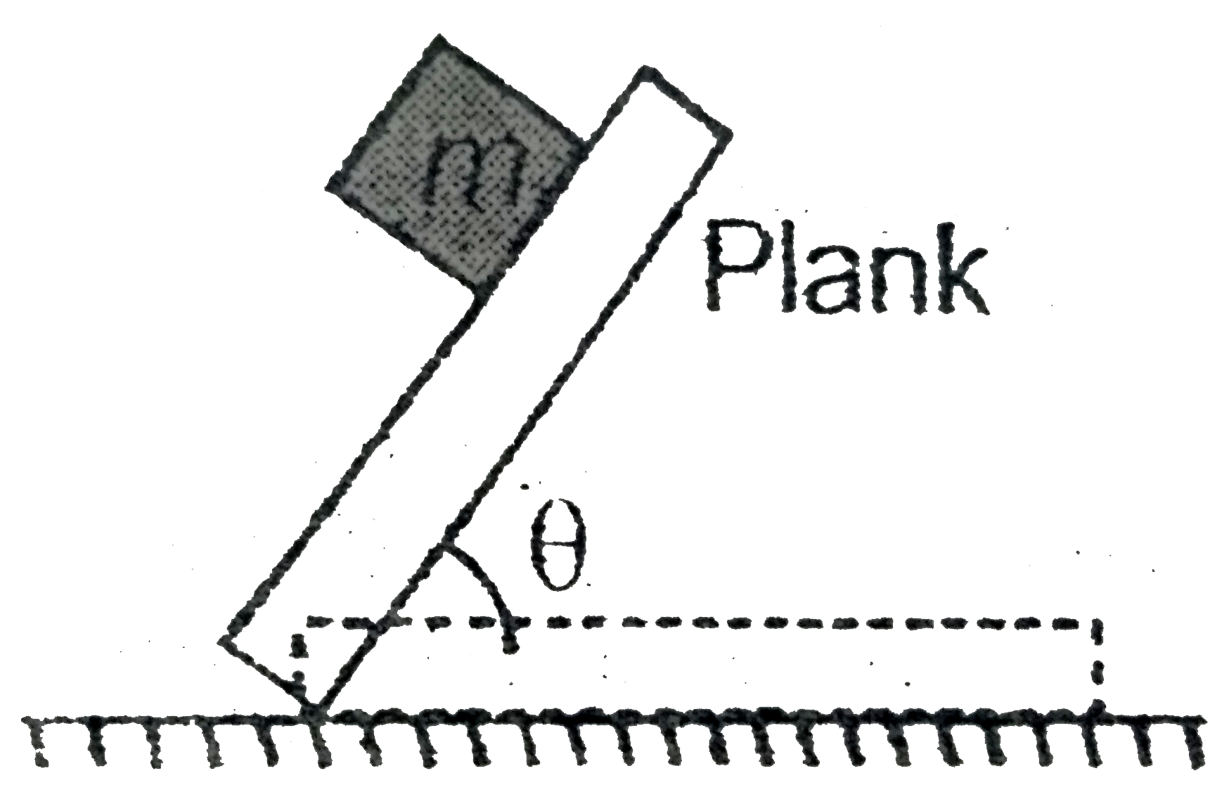
View SolutionA block of mass m is kept on a plank . The coefficient of friction between the plank and block is 1. The plank is slowly raised from one end so that it makes angle θ with horizontal . The forces of friction acting on the plank , when θ=30∘andθ60∘ are respectively,
View SolutionA rough horizontal plate rotates with angular velocity ω about a fixed vertical axis. A particle or mass m lies on the plate at a distance 5a4 from this axis. The coefficient of friction between the plate and the particle is 13 . The largest value of ω2 for which the particle will continue to be at rest on the revolving plate is
View Solution
A horizontal plank having mass m lies on a smooth horizontal surface. A sphere of same mass and radius r is spined to angular frequency ω0 and gently placed on the plank as shown in the figure. If coefficient of friction between the plank and the sphere is μ. Find the distance moved by the plank till sphere starts pure rolling on the plank. the plank is long enough.
View Solution