The pulley shown in figure has a moment of inertias I about its xis and mss m. find the tikme period of vertical oscillastion of its centre of mass. The spring has spring constant k and the string does not slip over the pulley.
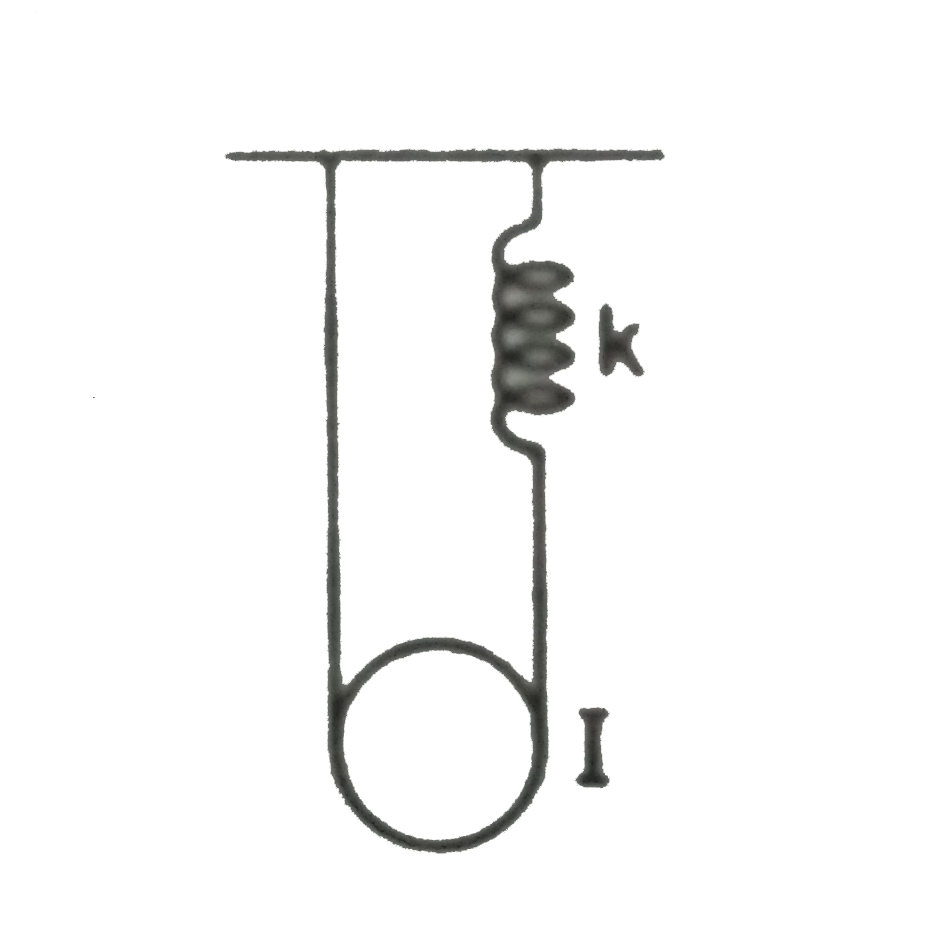
For rotatiobnal equation the tension in spring on both sides must be same .
Let T be the tension in the string in equilibrium position and l0 the extension of spring . Then for equilibrum of any part of spring on RHS.
2T=mg⇒2kl0=mgorl0=mg2K
For translational equation of pulley l0=mg2K
Thus when pulley attains equilibrium , the spring is streched by a distance
l0=mg2K (i)
Now suppose that the pulley is down a little and released. The pulley starts up and down oscillation . Let y be instant neous displacement of center of pulley from equilibrium. Then total increase in length of (string + spring) is 2y (y to the left of pulley and y to the right).
As steing is inextensible, total extension of spring is 2y.
As pulley also ratates energy of system is
E=12lω2+12mv2−mgy+12K(l0+2y)2
But ω=vr
E=12lv2r2+12K(l0+2y)2
=12(lr2+m)v2=mgy+12K(l0+2y)2
Asd total energy is constant (system is conservative)
dEdt=0
12(lr2+m)2vdvdt−mg(dv)dt+12K2(l0+2y),2dydt=0
and dydt=vanddvdt=ae≤rationa
and l0=mg2K
we get (lr2+m)a−mg+2K(mg2k+2y)=0
a∝−y (ii)
As a∝−y, motion of pulley is SHM.
Standard equiation of SHM
a=−ω2y
Comparing Eqs, (ii) and (iii), ω2=4klr2+m
time period.
T=2πω=2π
⎷⎧⎪⎨⎪⎩lr2+m4K⎫⎪⎬⎪⎭=π
⎷⎧⎪⎨⎪⎩m+lr2K⎫⎪⎬⎪⎭
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Exercise 4.1
23 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Exercise 4.2
23 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Single correct anwer type
14 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
Similar Questions
The pulley shown in figure has a moment of inertias I about its axis and mass m. find the time period of vertical oscillation of its centre of mass. The spring has spring constant k and the string does not slip over the pulley.

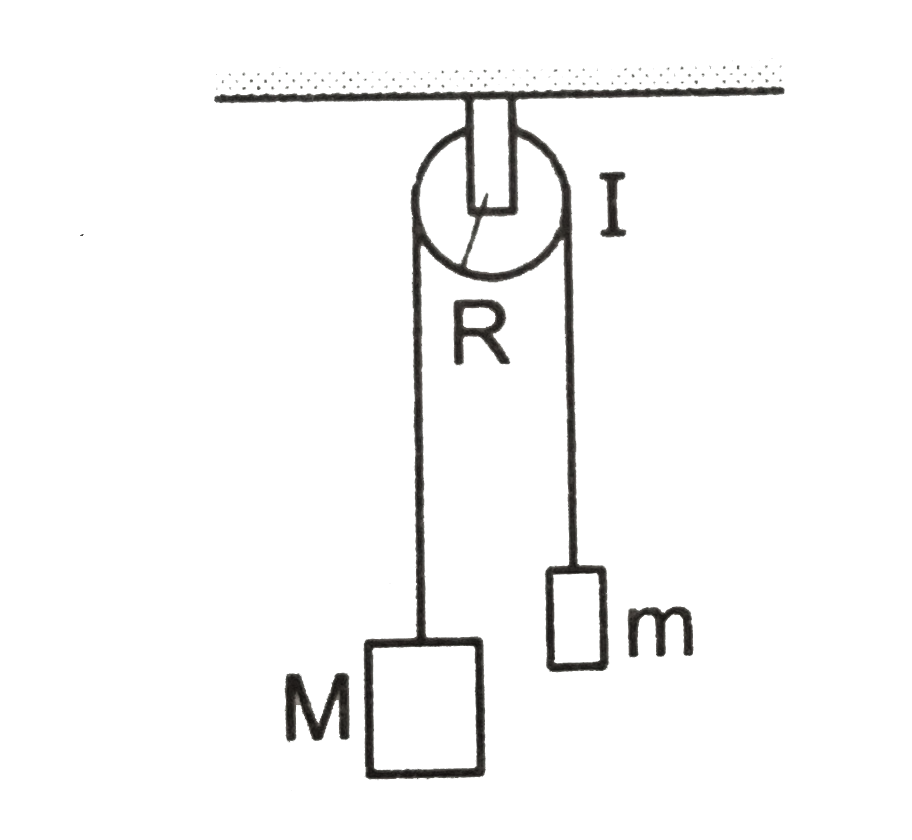
View SolutionThe pulley shown in figure has a moment of inertia I about it's axis and its radius is R. Find the magnitude of the acceleration of the two blocks. Assume that the string is light and does not slip on the pulley.
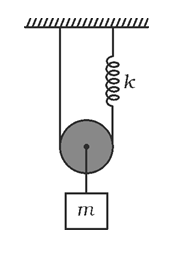
View SolutionFind the time period of oscillation of block of mass m. Spring, and pulley are ideal. Spring constant is k.
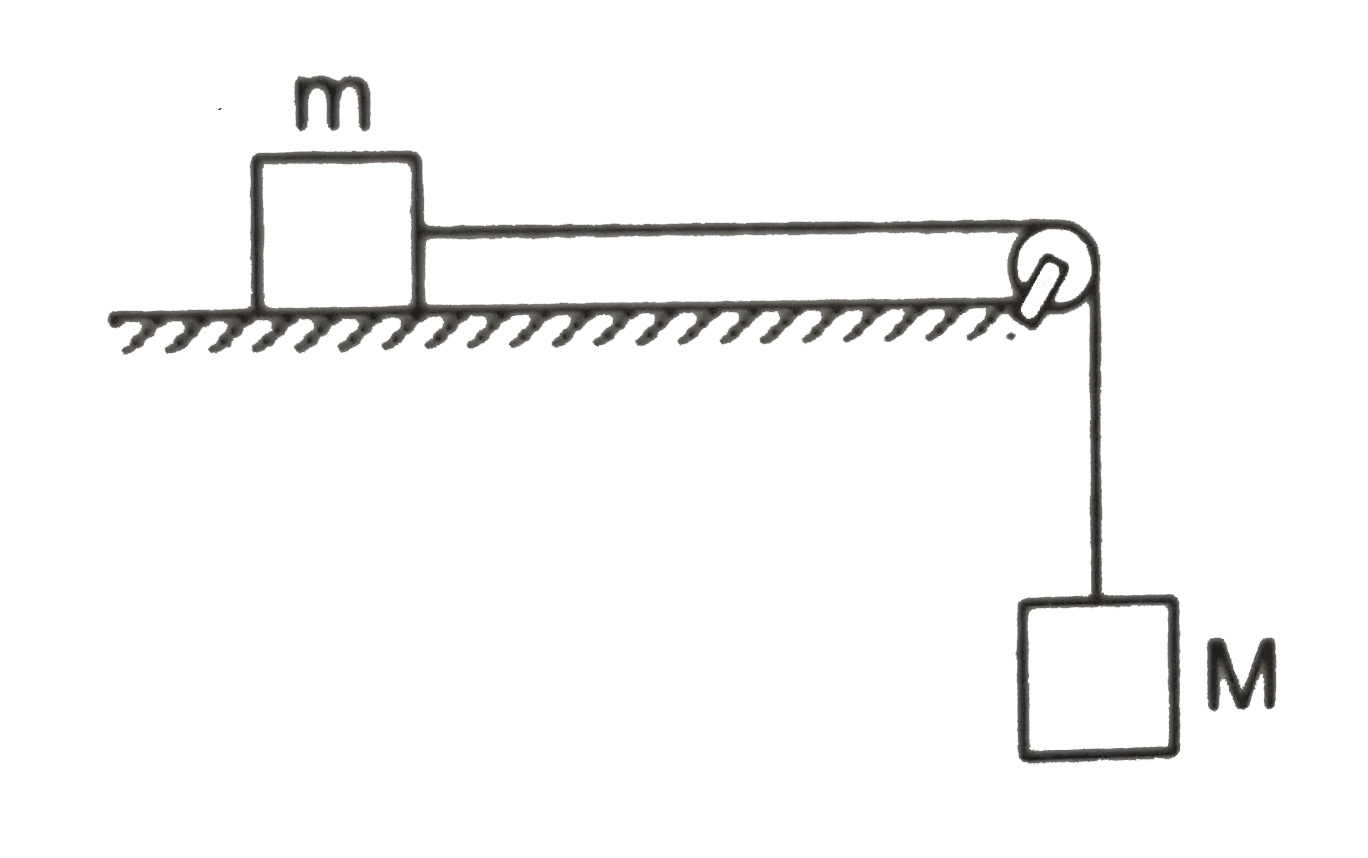
View SolutionFigure shows two blocks of masses m and M connected by a string passing over a pulley. The horizontal table over which the mass m slides is smooth. The pulley has a radius r and moment of inertia I about its axis and it can freely rotate about this axis. Find the acceleration of the mass M assuming that the string does not slip on the pulley.
View SolutionConsider the situation shown in the figure. A mass is hanging from a inextensible string which is passing over a pulley. The pulley itself is attached to a massless spring of stiffness k as shown in the figure. Find the time period of vertical oscillations of mass m if pulley is slightly displaced from its mean position. Assume that string does not slip over pulley.
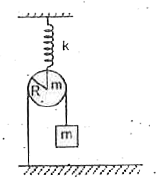
View SolutionIn the situation as shown in figure time period of small vertical oscillation of block will be - (String, springs and pulley are ideal)
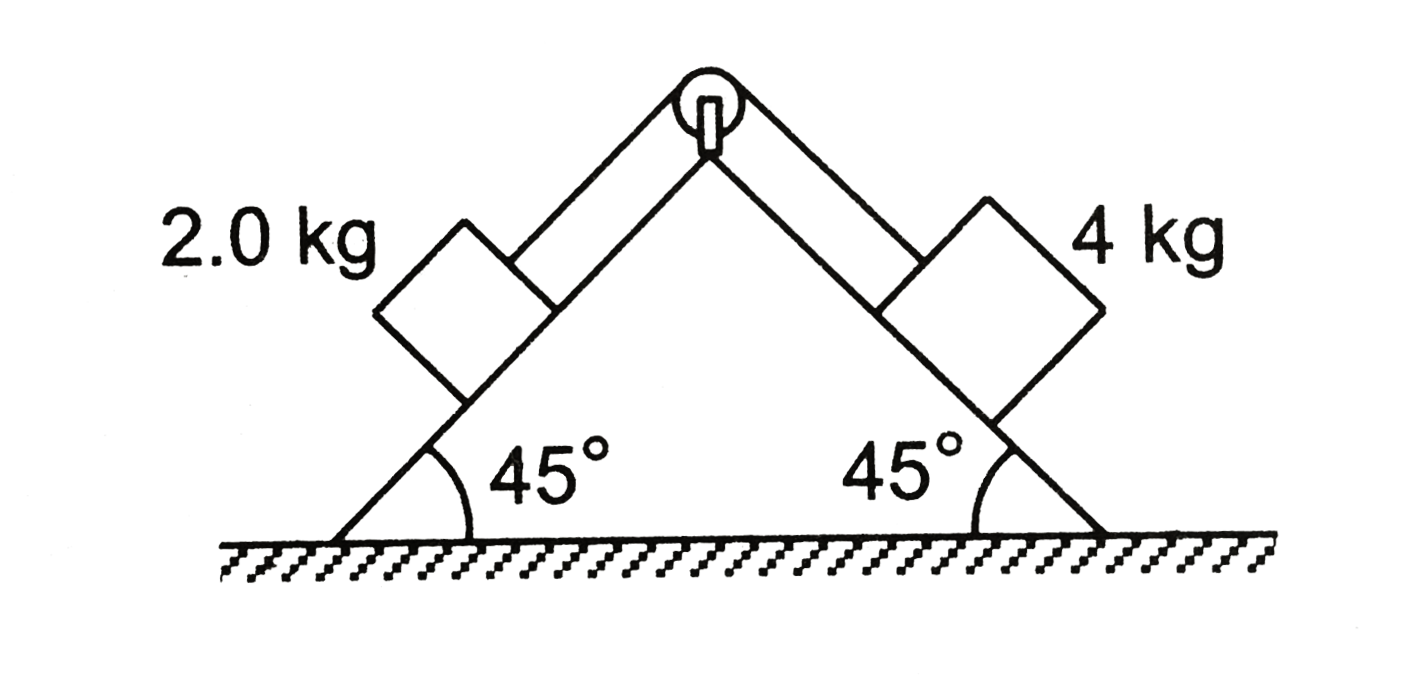
View SolutionThe pulley shown in figure has a radius 10 cm and moment of inertia 0.5 kg-m^2 about its axis. Assuming the inclined planes to be frictionless, calculate the acceleration of the 4.0 kg block.
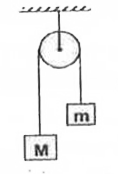
View SolutionTwo masses m and M(m<M) are joined by a light string passing over a smooth and light pulley (as shown)
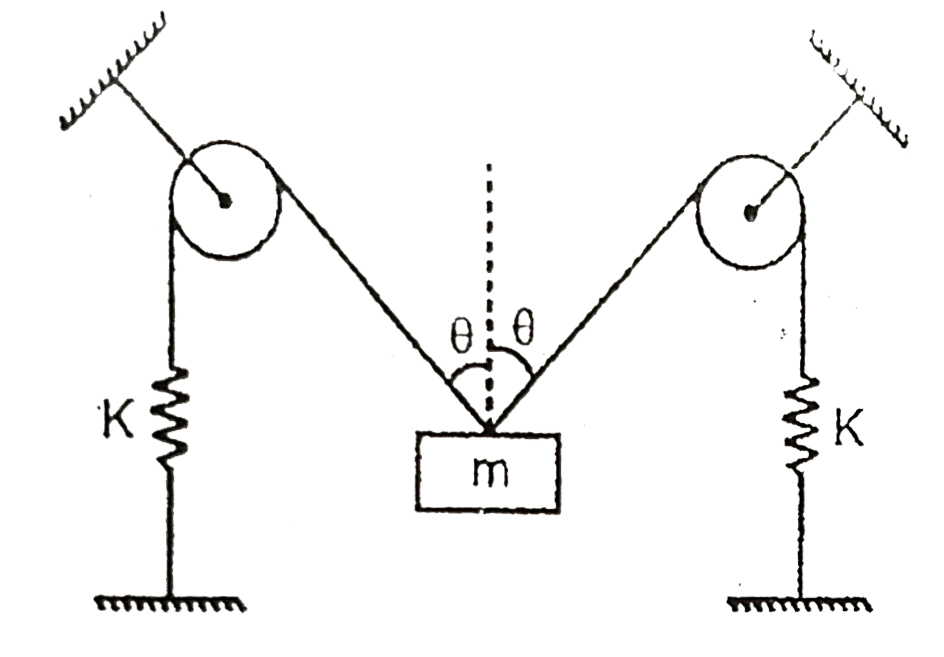
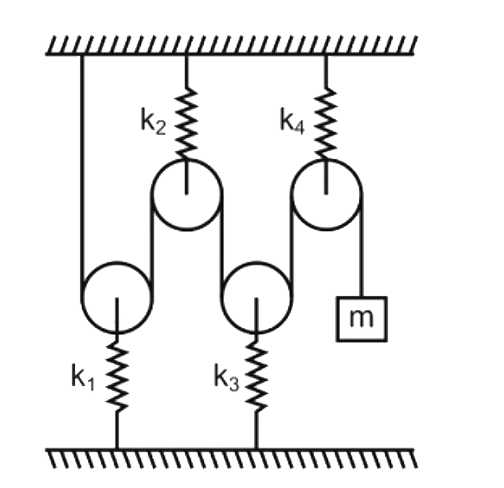
View SolutionIn the arrangement shown in the diagram, pulleys are small and springs are ideal. k1=k2=k3=k4=10Nm−1 are force constants of the springs and mass m=10kg. If the time period of small vertical oscillations of the block of mass m is given by 2πx seconds, then find the value of x.
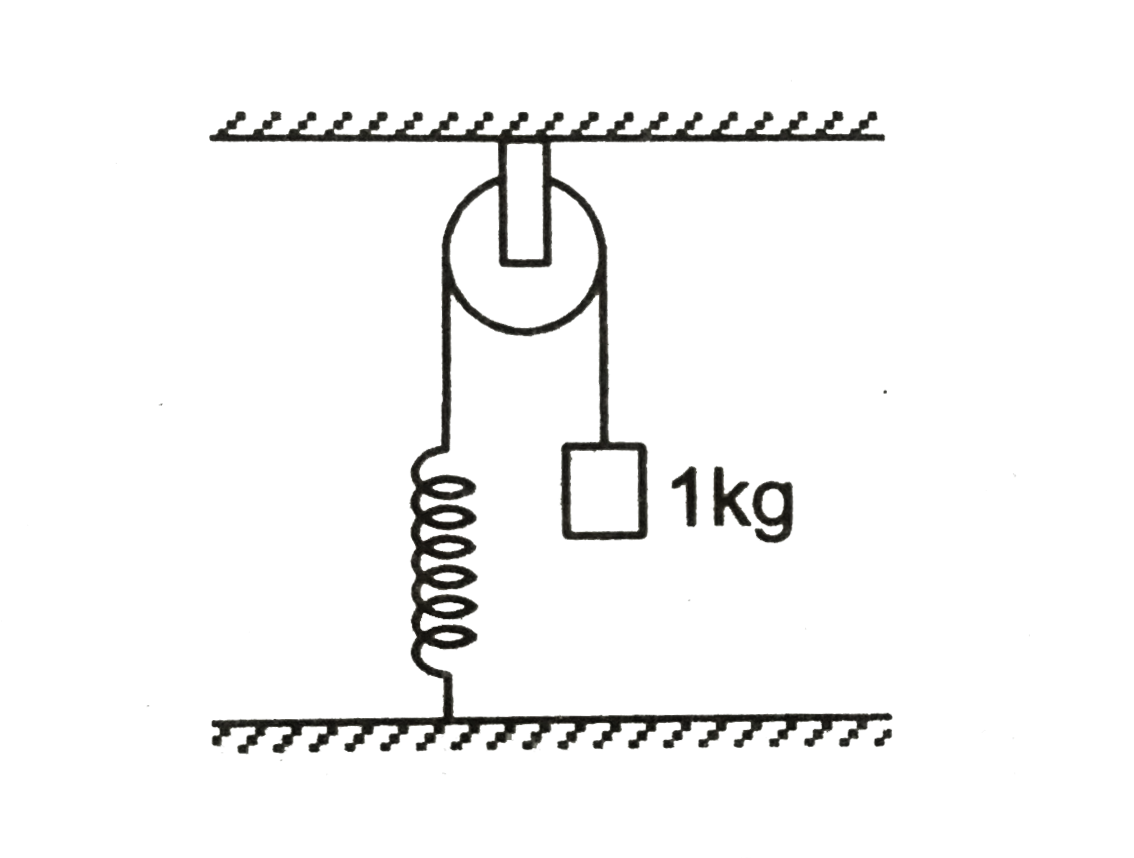
View SolutionThe pulley shown in figure has a radius of 20 cm and moment of inertial 0.2 kg-m^2. The string going over it is attached at one end to a vertical sprign of spring constant 50 N/m fixed from below and supports a 1 kg mas at other end. The system is released from rest with the spring at its natural length. Find the speed of the block when it has desceds through 10 cm. Take g=10ms2.
View Solution
