A simple pendulum of length L and mass m has a spring of force constant k connected to it at a distance h below its point of suspension. Find the frequency of vibrations of the system for small values of amplitude.

Video Solution

Text Solution

Verified by Experts

The frequency of vibration should be greater than that of a simple pendulum since the spring addsan additional restoring force.
$f > \frac{1}{2 π} \sqrt{\frac{g}{l}}$

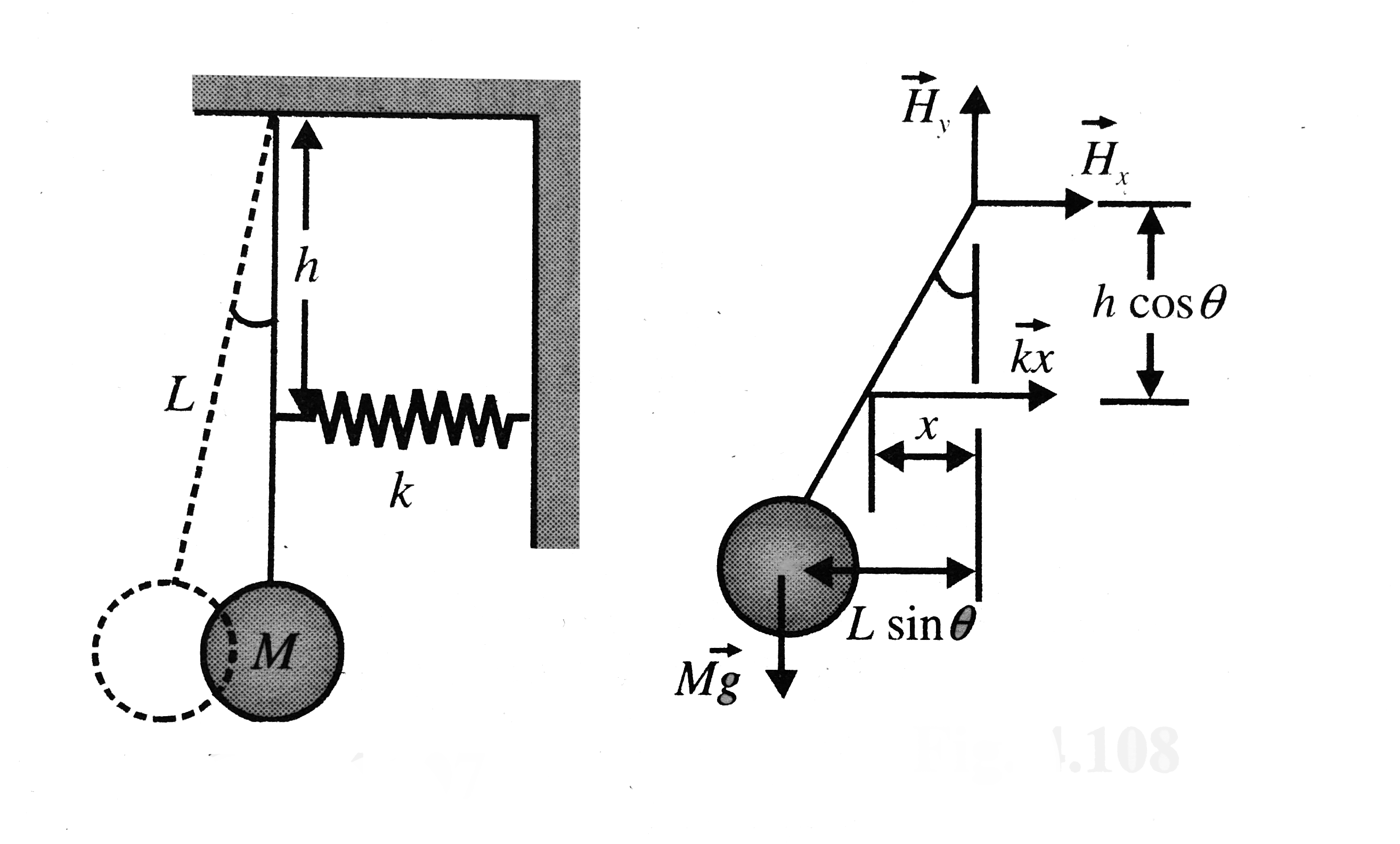
We can find the frequency $ω$ , which is found in equation for angular SHM : $d^{2} θ / {d t}^{2} = - ω^{2} θ$ . The angular acceleration can be found from analysing the tarque acting on the pendulum.
Fior the pendulum (see sketch)
$Σ τ = l α and d^{2} θ / {d t}^{2} = - α$
The negative sign appears because positive $θ$ is measured clockwise in the picture. We take torque around the point of suspension:
$Σ τ = M g L \sin θ + k x h \cos θ = l α$
For small amplitude vibrations, use the approximations:
$\sin θ = \cos θ \approx 1, and x = h \tan θ = h θ$
Therefore, with $l = m L^{2}$ .
$\frac{d^{2} θ}{{d t}^{2}} = - ω^{2} θ$
With angular frequency $ω = \sqrt{\frac{M g L + k h^{2}}{M L^{2}}} = 2 π f$
The frequency is $f = \frac{ω}{2 π} = \frac{1}{2 π} \sqrt{\frac{M g L + k h^{2}}{M L^{2}}}$

|

Updated on:21/07/2023

Class 11 PHYSICS SIMPLE HARMONIC MOTION

Topper's Solved these Questions

Similar Questions

CENGAGE PHYSICS ENGLISH-LINEAR AND ANGULAR SIMPLE HARMONIC MOTION-Solved Example

Home
Ask Doubt
Profile