A certain of a perfect gas is enclosed in a cylinder of volume V0 fitted with a smooth heavy piostion of mass m and area a. The piston is displaced through a small distance downwards so as to compress the gas isother mally , and then it is left free to go show that it performs SHM and also find its period . Take the atmospheric pressure as Pa→m.
To solve the problem, we will follow these steps:
Step 1: Understand the system and initial conditions
We have a cylinder with a piston that contains a perfect gas. The piston is initially at rest, and the system is in equilibrium with atmospheric pressure acting on one side and the gas pressure on the other side. The initial pressure of the gas is denoted as P and the atmospheric pressure as Patm.
Step 2: Establish the equilibrium condition
At the mean position (equilibrium position), the forces acting on the piston are balanced. Therefore, we can write the equation:
Patm⋅A+mg=P⋅A
This can be rearranged to:
P⋅A=Patm⋅A+mg(1)
Step 3: Displace the piston and analyze the new condition
When the piston is displaced downwards by a small distance x, the new volume of the gas becomes:
V=V0−A⋅x
Using the ideal gas law for isothermal conditions, we have:
P1V1=P2V2
Substituting the initial and final conditions:
P⋅V0=P2⋅(V0−A⋅x)
From this, we can solve for P2:
P2=P⋅V0V0−A⋅x
Step 4: Apply the binomial approximation
For small displacements x, we can use the binomial expansion:
1V0−A⋅x≈1V0(1+A⋅xV0)
Thus,
P2≈P+P⋅A⋅xV0
Step 5: Calculate the restoring force
The restoring force acting on the piston when displaced is given by:
Frestoring=P2⋅A−Patm⋅A−mg
Substituting P2:
Frestoring=(P+P⋅A⋅xV0)A−Patm⋅A−mg
Using equation (1) to substitute P⋅A:
Frestoring=P⋅A2V0⋅x
This shows that the restoring force is proportional to −x, confirming that the motion is simple harmonic.
Step 6: Find the acceleration
The acceleration a can be found using Newton's second law:
F=ma⟹a=Frestoringm
Substituting for Frestoring:
a=P⋅A2V0⋅m⋅x
Step 7: Determine the time period of SHM
The time period T of simple harmonic motion is given by:
T=2π√xa
Substituting for a:
T=2π√V0P⋅A2
Final Result
Thus, we have shown that the piston performs simple harmonic motion and the time period T is given by:
T=2π√V0P⋅A2
We have a cylinder with a piston that contains a perfect gas. The piston is initially at rest, and the system is in equilibrium with atmospheric pressure acting on one side and the gas pressure on the other side. The initial pressure of the gas is denoted as P and the atmospheric pressure as Patm.
At the mean position (equilibrium position), the forces acting on the piston are balanced. Therefore, we can write the equation:
Patm⋅A+mg=P⋅A
This can be rearranged to:
P⋅A=Patm⋅A+mg(1)
When the piston is displaced downwards by a small distance x, the new volume of the gas becomes:
V=V0−A⋅x
Using the ideal gas law for isothermal conditions, we have:
P1V1=P2V2
Substituting the initial and final conditions:
P⋅V0=P2⋅(V0−A⋅x)
From this, we can solve for P2:
P2=P⋅V0V0−A⋅x
For small displacements x, we can use the binomial expansion:
1V0−A⋅x≈1V0(1+A⋅xV0)
Thus,
P2≈P+P⋅A⋅xV0
The restoring force acting on the piston when displaced is given by:
Frestoring=P2⋅A−Patm⋅A−mg
Substituting P2:
Frestoring=(P+P⋅A⋅xV0)A−Patm⋅A−mg
Using equation (1) to substitute P⋅A:
Frestoring=P⋅A2V0⋅x
This shows that the restoring force is proportional to −x, confirming that the motion is simple harmonic.
The acceleration a can be found using Newton's second law:
F=ma⟹a=Frestoringm
Substituting for Frestoring:
a=P⋅A2V0⋅m⋅x
The time period T of simple harmonic motion is given by:
T=2π√xa
Substituting for a:
T=2π√V0P⋅A2
Thus, we have shown that the piston performs simple harmonic motion and the time period T is given by:
T=2π√V0P⋅A2
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Exercise 4.123videos
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Exercise 4.223videos
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Single correct anwer type14videos
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger11videos
KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type3videos
MISCELLANEOUS KINEMATICS
Similar Questions
An ideal gas is enclosed in a cylinder fitted with a frictionless piston. The piston is connected with a light rod to one plate of capacitor whose other plate is fixed as shown. Initially volume of the gas inside the cylinder is V0 Atmospheric pressure is P0 separation between the plates is L, area of the piston as well as of the capacitor plates is A and emf of battery is ε . A heater supplies heat to the gas so that pressure of the gas is given as P=P0−nε0ε2L2 when piston is displaced by a distance L2 . Find value of n.
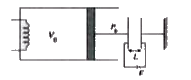 View Solution
View Solution2.00 mole of a monatomic ideal gas (U=1.5nRT) is enclosed in an adiabatic, fixed , vertical cylinder fitted with a smooth, light adiabatic piston. The piston is connected to a vertical spring of spring constant 200Nm−1 as shown in .the area of cross section of the cylinder is 20.0cm2. initially, the spring is at its natural length and the temperature of the gas is 300K at its natural length. the atmosphere pressure is 100 kPa. the gas is heated slowly for some time by means of an electric heater so as to move the position up through 10 cm. find (a) the work done by the gas (b) the final temperature of the gas and (c ) the heat supplied by the heater.
 View Solution
View SolutionA smooth vertical tube having two different cross sections is open from both the ends but closed by two sliding pistions as shown in Fig. and tied with an inextensible string. One mole of an ideal gas is enclosed between the piston The difference in cross-sectional areas of the two pistons is given ΔS. The masses of piston are m1 and m2 for larger and smaller one, respectively. Find the temperature by which tube is raised so that the pistons will be displaced by a distance l. Take atmospheric pressure equal to P0
 View Solution
View SolutionA smooth vertical tube having two different cross sections is open from both the ends but closed by two sliding pistions as shown in Fig. and tied with an inextensible string. One mole of an ideal gas is enclosed between the piston The difference in cross-sectional areas of the two pistons is given ΔS. The masses of piston are m1 and m2 for larger and smaller one, respectively. Find the temperature by which tube is raised so that the pistons will be displaced by a distance l. Take atmospheric pressure equal to P0
 View Solution
View SolutionA vertical thermally insulated cylinder of volume V contain n moles of an ideal monoatomic gas under a weightless piston. A load of weight W is placed on the piston as a result of which the piston is displaced. If the initial temp of the gas is 300K, area of piston is A and atmospheric pressure P0. (take W=P0A). Determine the value of final temperature of the gas
View SolutionA piston of mass m divides a cylinder containing gas into two equal parts. Suppose the piston is displaced to the left to a distance x and let go Fig. Assuming the process to take place at a constant temperature, find the frequency of the piston's oscillations.
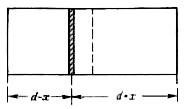 View Solution
View SolutionTwo moles of an ideal gas are contained in a vertical cylinder with a frictionless piston. The piston is slowly displaced so that expansionin gas is isothermal at temperature T0=400K. find the amount of work done in increasing the volume to 3 times.t ake atmospheric pressure =105N/m2
View SolutionThe fixed non-conducting cylinder shown in figure has a noconducting heavy piston of mass M that can slide without friction. The area of piston is S and the cylinder is filled with an ideal gas (λ=1.5) with an initial volume V and an initial pressure P. Assume that the outside pressure on the piston is zero (vaccum). (Neglect acceleration due to gravity).
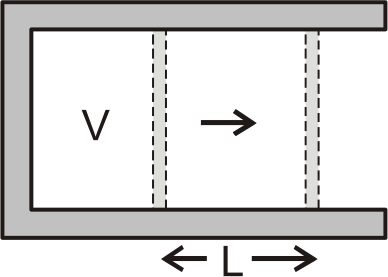
For the temperature of the gas to drop to one half of its original value. the piston will have to move by a distance:View SolutionThe fixed non-conducting cylinder shown in figure has a noconducting heavy piston of mass M that can slide without friction. The area of piston is S and the cylinder is filled with an ideal gas (λ=1.5) with an initial volume V and an initial pressure P. Assume that the outside pressure on the piston is zero (vaccum). (Neglect acceleration due to gravity).
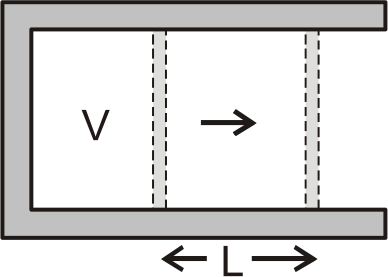
After the piston has moved by distance S. Its velocity is:View SolutionThe fixed non-conducting cylinder shown in figure has a noconducting heavy piston of mass M that can slide without friction. The area of piston is S and the cylinder is filled with an ideal gas (λ=1.5) with an initial volume V and an initial pressure P. Assume that the outside pressure on the piston is zero (vaccum). (Neglect acceleration due to gravity).
The initial acceleration of piston is:View Solution
