2.00 mole of a monatomic ideal gas (U=1.5nRT) is enclosed in an adiabatic, fixed , vertical cylinder fitted with a smooth, light adiabatic piston. The piston is connected to a vertical spring of spring constant 200Nm−1 as shown in .the area of cross section of the cylinder is 20.0cm2. initially, the spring is at its natural length and the temperature of the gas is 300K at its natural length. the atmosphere pressure is 100 kPa. the gas is heated slowly for some time by means of an electric heater so as to move the position up through 10 cm. find (a) the work done by the gas (b) the final temperature of the gas and (c ) the heat supplied by the heater.

(a) the force by the gas on the piston is
F=p0A+ks
Where p0=100kPa is the atmospheric pressure, A=20cm2 is the area of cross section, k=200Nm1 is the spring constant and x is the compression of the spring. The work done by the gas as the piston moves throughl=10cmis<br>W=int_(0)^(l) Fdx<br>=p_(0)Al+(1)/(2)kl^(2)<br>=(100×103Pa)×(20×10−4m2)×(10×10−2m)
+12(200Nm−1)×(100×10−4m2)
=20J+1J=21J.
(b) The initial tempreture is T1=300K. Let the final tempreture be T2 We have
nRT1=p0V0
and nRT2=pV_(2)=(p0+klA)(V0+Al)
=nRT1+p0Al+kl2+(klnRT1)/(Ap_(0))<br>or,T_(2)=T_(1)+(p_(0)Al+kl^(2))/(nR)+(klT_(1))/(Ap_(0))<br>=(300 K)+(20 J+2 J)/((2.0 mol)(8.3 JK^(-1) mol^(-1))<br>+((200 Nm^(-1))xx(10xx10^(-2)m)xx(300 K))/((20xx10^(4)m^(2))xx(100xx10^(3)Pa))<br>=300 K+1.325 K+30 K<br>=331 K.<br>(c)the∫ernale≠rgyisU=1.5nRT.<br>thechan≥∈∫ernale≠rgyis<br>DeltaU=1.5nRDeltaT<br>=1.5xx(2.00 mol)xx(8.3 J K^(-1) mol^(-1)xx(31 K)<br>=772 J
From the first law,
ΔQ=ΔU+ΔW
772J+21J=793J.
Topper's Solved these Questions
Similar Questions
Method 3 of W
Mass of a piston shown in Fig. is m and area of cross-section is A. Initially spring is in its natural length. Find work done by the gas.
 View Solution
View SolutionAn ideal monoatomic gas is enclosed in a fixed horizontal adiabatic cylinder of cross sectional area A. The cylinder is fitted with an adiabatic piston of mass m (attached to one end of a spring as shown) which can move horizontally without friction inside the cylinder. In equilibrium, the spring is in natural length and pressure and volume are P0 and V0 respectively. The piston is slightly displaced from equilibrium and released. Then, frequency of small oscillation is
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Two moles of an ideal monoatomic gas occupy a volume 2V at temperature 300K, it expands to a volume 4V adiabatically, then the final temperature of gas is
Aa.179 KBb.189 KCc.199 KDd.219 K
A diatomic gas is enclosed in a vessel fitted with massless movable piston. Area of cross section of vessel is 1m2. Initial height of the piston is 1m (see the figure). The initial temperature of the gas is 300K. The temperature of the gas is increased to 400K, keeping pressure constant, calculate the new height of the piston. The piston is brought to its initial position with no heat exchange. Calculate the final temperature of the gas. You can leave answer in fraction.
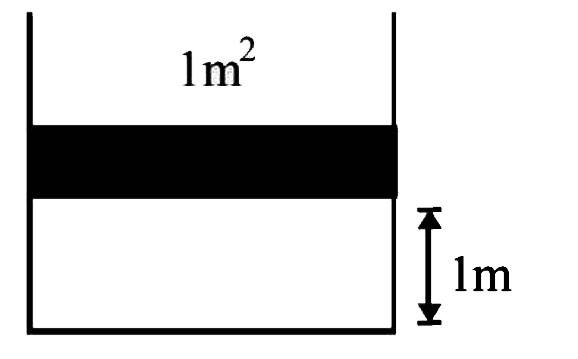 View Solution
View SolutionThe piston cylinder arrangement shown contains a diatomic gas at temperature 300 K The cross sectinal area of the cylinder is 1m2. Initially the height of the piston above th base of the cyclinder is 1 m. The temperature is now raised to 400 K at constant pressure. There is no heat loss in the process..
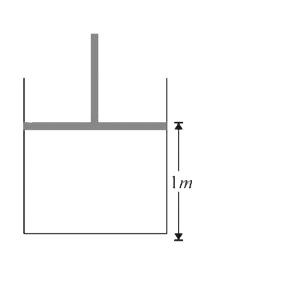
Find the new height (in m) of the piston above the base of the cylinder.View SolutionAn ideal gas enclosed in a cylinder fitted with a frictionless and weightless piston, pushes it outside. What would be the sign convention for the work ?
View SolutionAn ideal gas enclosed in a cylinder fitted with a frictionless and weightless piston, pushes it outside. What would be the sign convention for the work ?
View SolutionThe air tight and smooth piston of a cylindrical vessel are connected with a string as shown. Initially pressure and temperature of the gas are P0 and T0. The atmospheric pressure is also P0. At a later time, tension in the string is 38P0A where A is the cross-sectional are of the cylinder. at this time, the temperature of the gas has become.
 View Solution
View SolutionA fixed container is fitted with a piston which is attached to a spring of spring constant k. The other and of the spring is attached to a rigid wall. Initially the spring is in its natural length and the length of container between the piston and its side wall is L. Now an dideal diatomic gas is slowly filled in the container so that the piston moves quasistatically. It pushed the piston by x so that the spring now is compressed by x. The total rotaional kinetic energy of the gas molecules in terms of the displacement x of the piston is (there is vacuum outside the container)
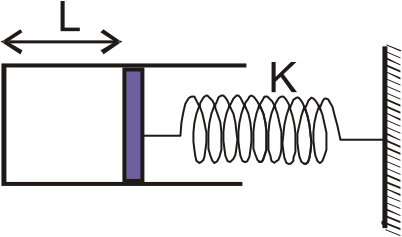 View Solution
View SolutionTwo cylinders A and B fitted with pistons contain equal amounts of an ideal diatomic gas at 300K. The piston of A is free to move, while that B is held fixed. The same amount of heat is given to the gas in each cylinder. If the rise in temperature of the gas in A is 30K, then the rise in temperature of the gas in B is
View Solution
