Figure Shows a process ABCA performed on an ideal gas. Find the net heat given to the system during the process.
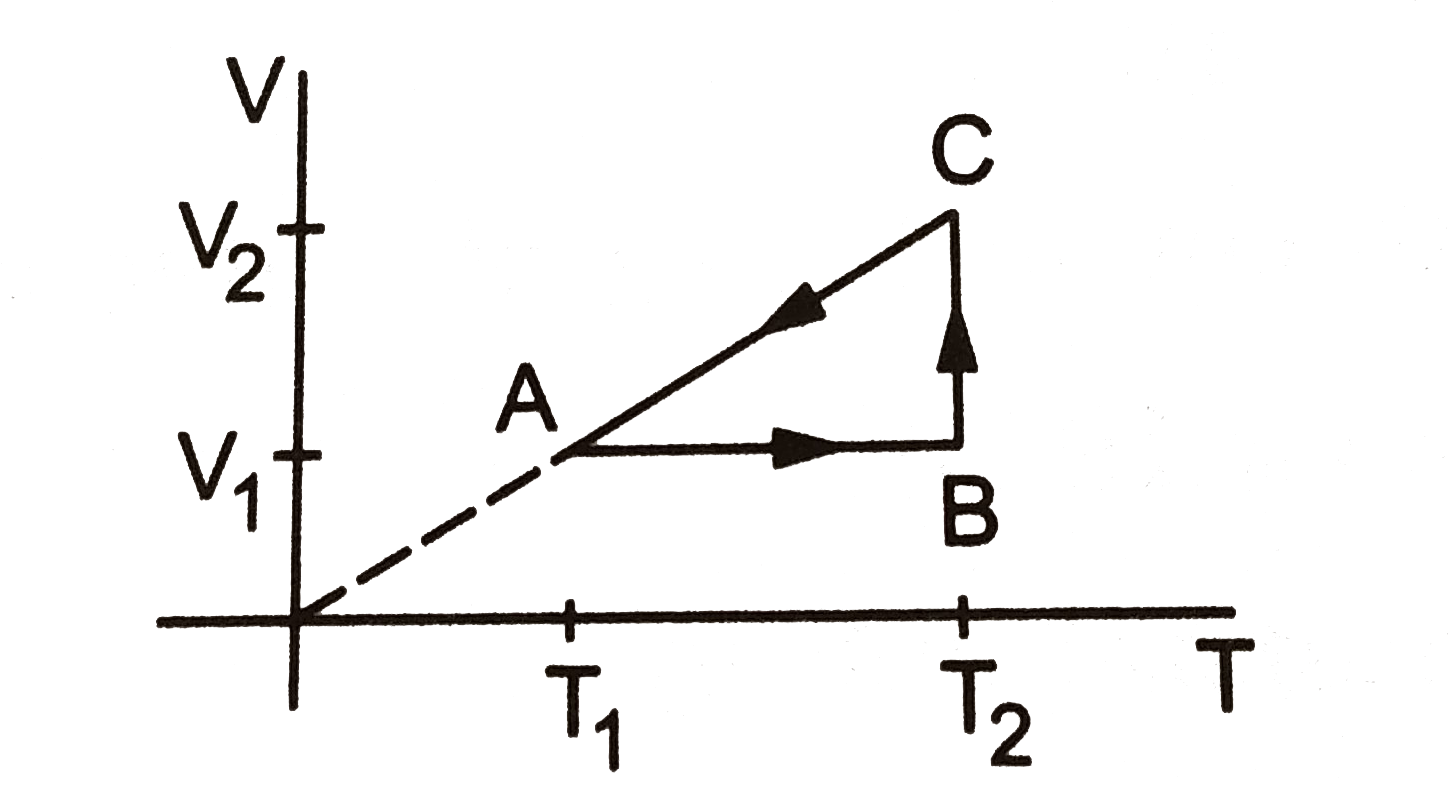
As the process is cycle, the change in internal energy is zero. The heat given to the system is then equal to the work done byh it.
The work done in part ABisW1=0 as the volume remains constant. The part BC represent an isothermal procces so that the work done by the gas during this part is
W2=nRT2In(V2/V1)
during the part CA,
V∝T.
so, V/T is constant and hence,
p=nRTV is constant.
The work done by the gas during the part CA is theworkdo≠bythegasthepartCAis<br>W_(3)=p(V_(1)-V_(2))<br>=nRT_(1)-nRT_(2)<br>=-nR(T_(2)-T-(1).
The net work done by the gas in the process ABCA is
W=W_(1)+W_(2)+W_(3)=nR[T_(2)InV_(2)/V_(1)-(T_(2)-T_(1))].
The same amount of heat is given to the gas.
Topper's Solved these Questions
Similar Questions
Fig. shows a process ABCA performed on 1 mole of an ideal gas. Find the net heat supplied to the gaseous system during the process.

View SolutionDuring the process AB of an ideal gas

View SolutionDuring the process AB of an ideal gas

View SolutionAn ideal gas undergoes a process A→B→C shown in P−V graph. Then total heat given to the gas during the whole process (A→B→C) is n×104J, then n is:
View SolutionA diatomic gas done 80J work when expanded isobarically. Find the heat given to the gas during this process?
View SolutionFor an ideal gas, the specific heat capacity during an isentropic process is always
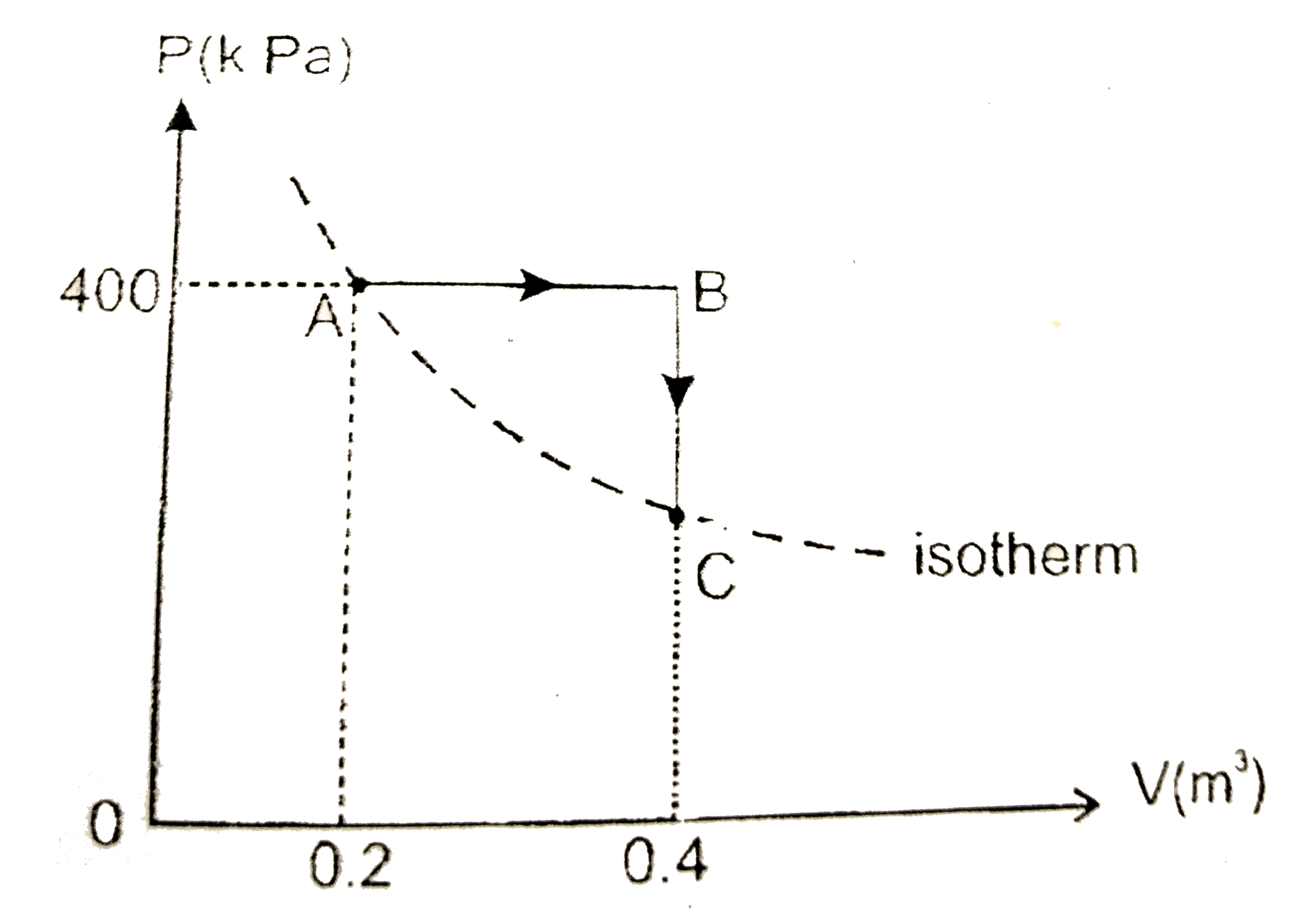
View SolutionIn figure, a cyclic process ABCA of 3 moles of an ideal gas is given. The temperature of the gas at B and C are 500k and 1000K respectively. If work done on the gas in process CA is 2500J then find the net heat absorbed or released by an idela gas. Take R=25/3J/mol−K.
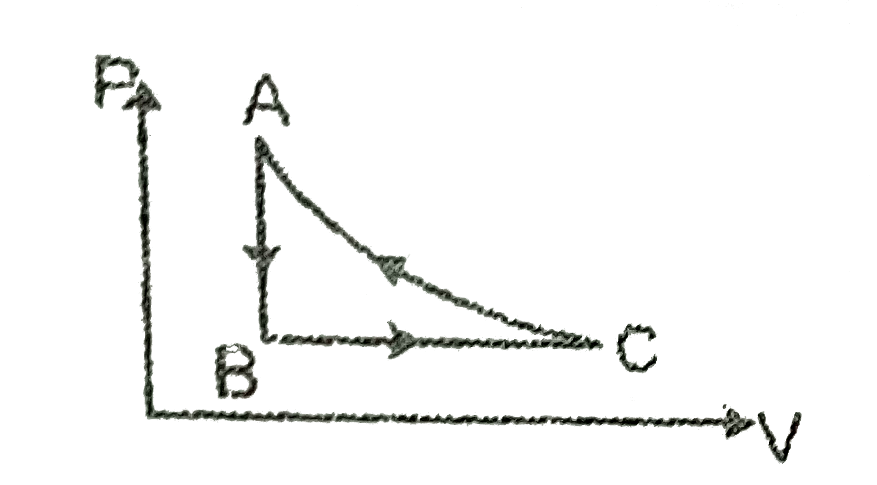
View SolutionA monatomic ideal gas undergoes the shown cyclic process in which path of the process 2→3 is a semicircle. If 2mol of gas is taken, find

Heat given to the system in semicircular process
View Solutiongraph of an ideal gas is as shown in figure.
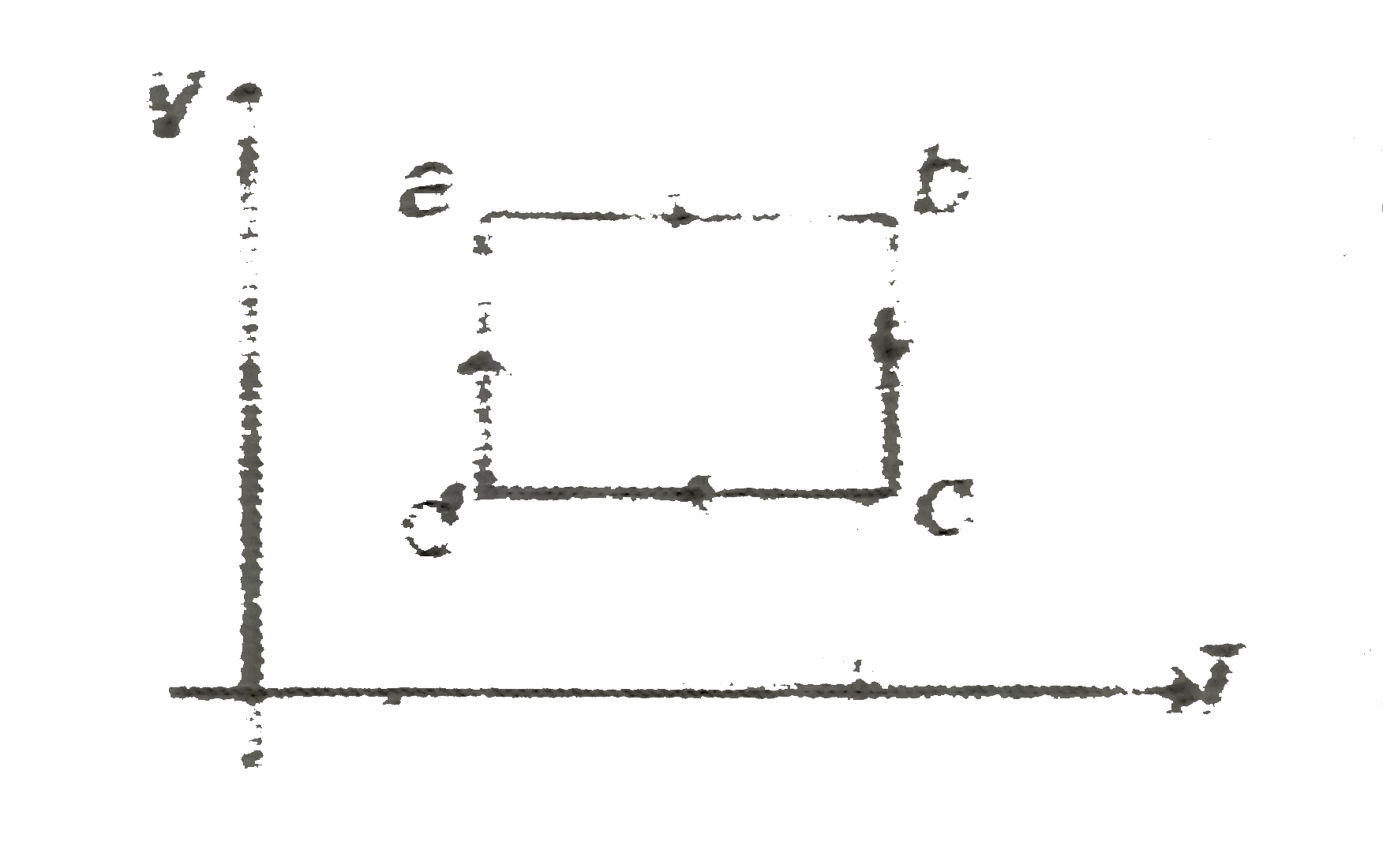
Heat is supplied to the gas in process (s).
View Solutionn' moles of an ideal gas undergoes a process A→B as shown in the figure. The maximum temperature of the gas during the process will be:
View Solution
