Question

A system can be taken from the initial state ${\displaystyle p_1,V_1}$ to the final state ${\displaystyle p_{2,V_2}}$ by two different methods, let ${\displaystyle \Delta Q\text{and}\Delta W}$ represent the heat given to the system and the work done by the system. Which of the following must be the same in both the method?

Options

A. `DeltaQ`
B. `DeltaW`
C. `DeltaQ+DeltaW`
D. `DeltaQ-DeltaW`.

Answer

D

Explanation

To solve the problem, we need to analyze the relationship between heat (ΔQ), work (ΔW), and internal energy (ΔU) as described by the first law of thermodynamics.

1. Understand the First Law of Thermodynamics:
The first law of thermodynamics states that the change in internal energy (ΔU) of a system is equal to the heat added to the system (ΔQ) minus the work done by the system (ΔW). This can be expressed mathematically as:
\( \Delta U = \Delta Q - \Delta W \)

2. Identify Internal Energy as a State Function:
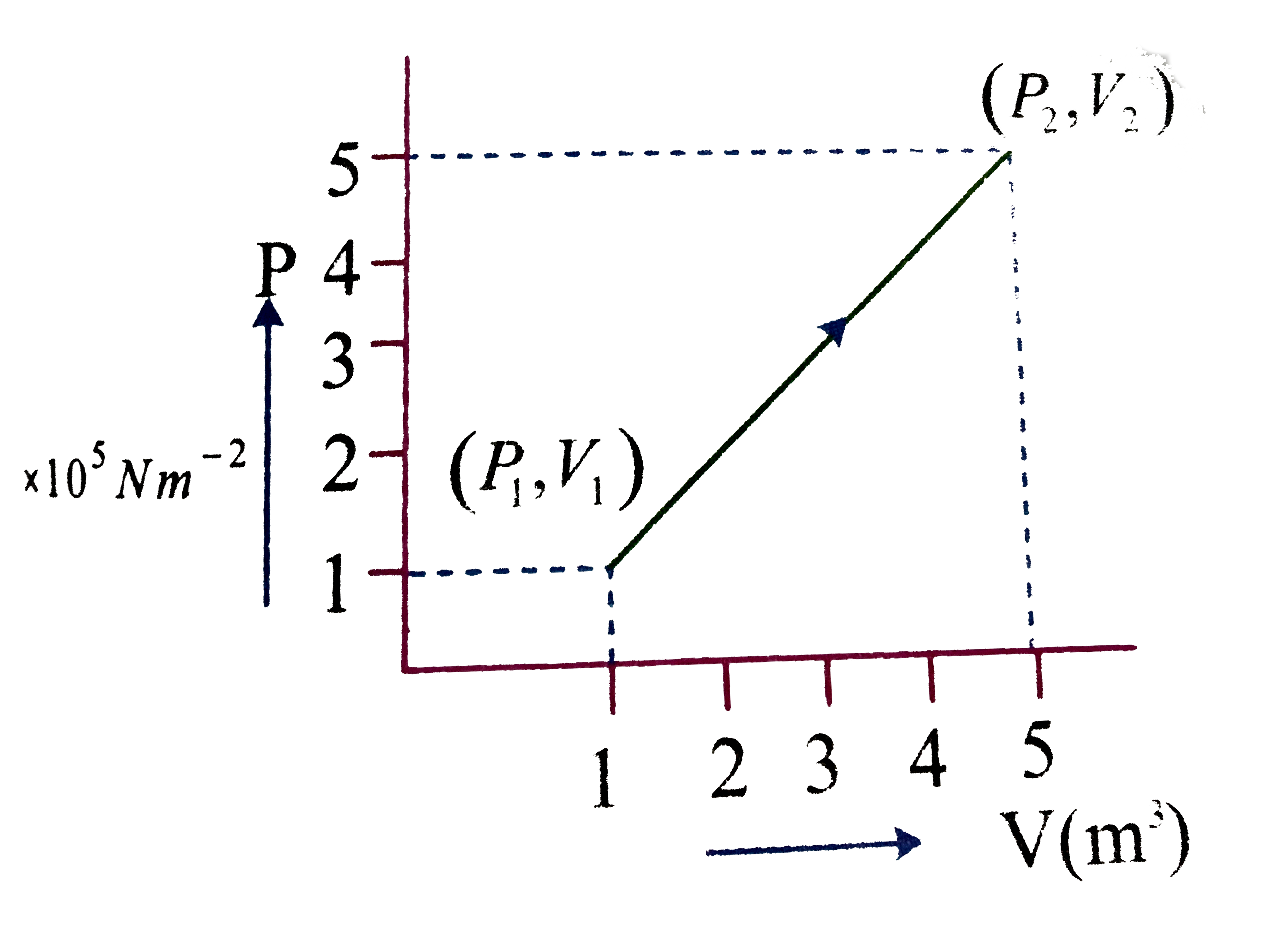
Internal energy (ΔU) is a state function, meaning it depends only on the initial and final states of the system, not on the path taken to get from one state to another. Therefore, if a system transitions from an initial state (p1, V1) to a final state (p2, V2), the change in internal energy will be the same regardless of the path taken.

3. Apply the Concept to Both Paths:
Since the internal energy change (ΔU) is the same for both paths (let's call them Path 1 and Path 2), we can write:
\( \Delta U_{Path1} = \Delta U_{Path2} \)

4. Relate ΔQ and ΔW for Both Paths:
From the first law, we can express the changes in internal energy for both paths:
\( \Delta U_{Path1} = \Delta Q_{Path1} - \Delta W_{Path1} \)
\( \Delta U_{Path2} = \Delta Q_{Path2} - \Delta W_{Path2} \)
Since ΔU is the same for both paths, we can set the two equations equal to each other:
\( \Delta Q_{Path1} - \Delta W_{Path1} = \Delta Q_{Path2} - \Delta W_{Path2} \)

5. Conclude About ΔQ and ΔW:
Rearranging the above equation gives us:
\( \Delta Q_{Path1} - \Delta Q_{Path2} = \Delta W_{Path1} - \Delta W_{Path2} \)
This indicates that ΔQ and ΔW can vary depending on the path taken, but the difference between the heat added and the work done must remain constant.

6. Final Conclusion:
Therefore, the only quantity that must be the same for both methods is the change in internal energy (ΔU), which can also be expressed as:
\( \Delta U = \Delta Q - \Delta W \)
Thus, the correct answer is:
\( \Delta Q - \Delta W \text{ must be the same for both methods.} \)

Answer:
The quantity that must be the same in both methods is \( \Delta Q - \Delta W \).

---