An ideal gas is taken from an initial state i to a final state f in such a way that the ratio of the pressure to the absolute temperature remains constant. What will be the work done by the gas ?
To solve the problem, we need to analyze the situation where an ideal gas is taken from an initial state (i) to a final state (f) while maintaining a constant ratio of pressure (P) to absolute temperature (T).
1. Understanding the Given Condition:
We are given that the ratio of pressure to absolute temperature remains constant. This can be mathematically expressed as:
PT=k
where k is a constant.
2. Using the Ideal Gas Law:
The ideal gas law is given by:
PV=nRT
Rearranging this, we can express pressure as:
P=nRTV
3. Relating Pressure and Temperature:
Since we have the condition PT=k, we can substitute for P:
nRT/VT=k
Simplifying this gives:
nRV=k
This implies that the volume V must also be constant since n and R are constants.
4. Change in Volume:
Since the volume remains constant during the process, we have:
ΔV=Vf−Vi=0
5. Calculating Work Done:
The work done by the gas during a process is given by the formula:
W=PΔV
Substituting ΔV=0 into the equation:
W=P×0=0
Conclusion:
The work done by the gas during this process is:
W=0
We are given that the ratio of pressure to absolute temperature remains constant. This can be mathematically expressed as:
PT=k
where k is a constant.
The ideal gas law is given by:
PV=nRT
Rearranging this, we can express pressure as:
P=nRTV
Since we have the condition PT=k, we can substitute for P:
nRT/VT=k
Simplifying this gives:
nRV=k
This implies that the volume V must also be constant since n and R are constants.
Since the volume remains constant during the process, we have:
ΔV=Vf−Vi=0
The work done by the gas during a process is given by the formula:
W=PΔV
Substituting ΔV=0 into the equation:
W=P×0=0
The work done by the gas during this process is:
W=0
Topper's Solved these Questions
Similar Questions
Knowledge Check
An ideal gas undergoes isothermal process from some initial state i to final state f. Choose the correct alternatives.
A1.dU=dQB2. dU=-dWC3. dU=0D4. dU=dW
An ideal gas change from state a to state b as shown in Fig. what is the work done by the gas in the process?

View SolutionWhen a sample of ideal gas is changed from an initial state to a final state, various curves can be plotted for the process like P-V curve, V-T curve,P-T curve etc.
For example, P-V curve for a fixed amount of an ideal gas at constant temperature is a rectangular hyperbola, V-T curve for a fixed amount of an ideal gas at constant volume is again a straight line. However, the shapes may vary if the constant parameters are also changed.
Now, answer the following questions :
Two moles of an ideal gas is changed from its initial state (16 atm, 6L) to final state (4 atm, 15L) in such a way that this change can be represented by a straight line in P-V curve.The maximum temperature attained by the gas during the above change is :(Take : R=112LatmK−1mol−1)
View SolutionTwo moles of an ideal monatomic gas is heated at constant pressure so that its temperature increases from 127∘C to 227∘C , then work done by gas
View SolutionAn ideal gas can be taken form initial state 1 to final state 2 by two different process. Let ΔQ and W represent the heat given and work done by the system. Then which quantities is/are same in both process (where ΔU= internal energy of gas)
View SolutionFor an ideal gas, consider only P−V work in going from an initial state X to the final state Z. The final state Z can be reached by either of the two paths shown in the figure. Which of the following choice(s) is (are) correct? [Take ΔS as change in entropy and w as work done]
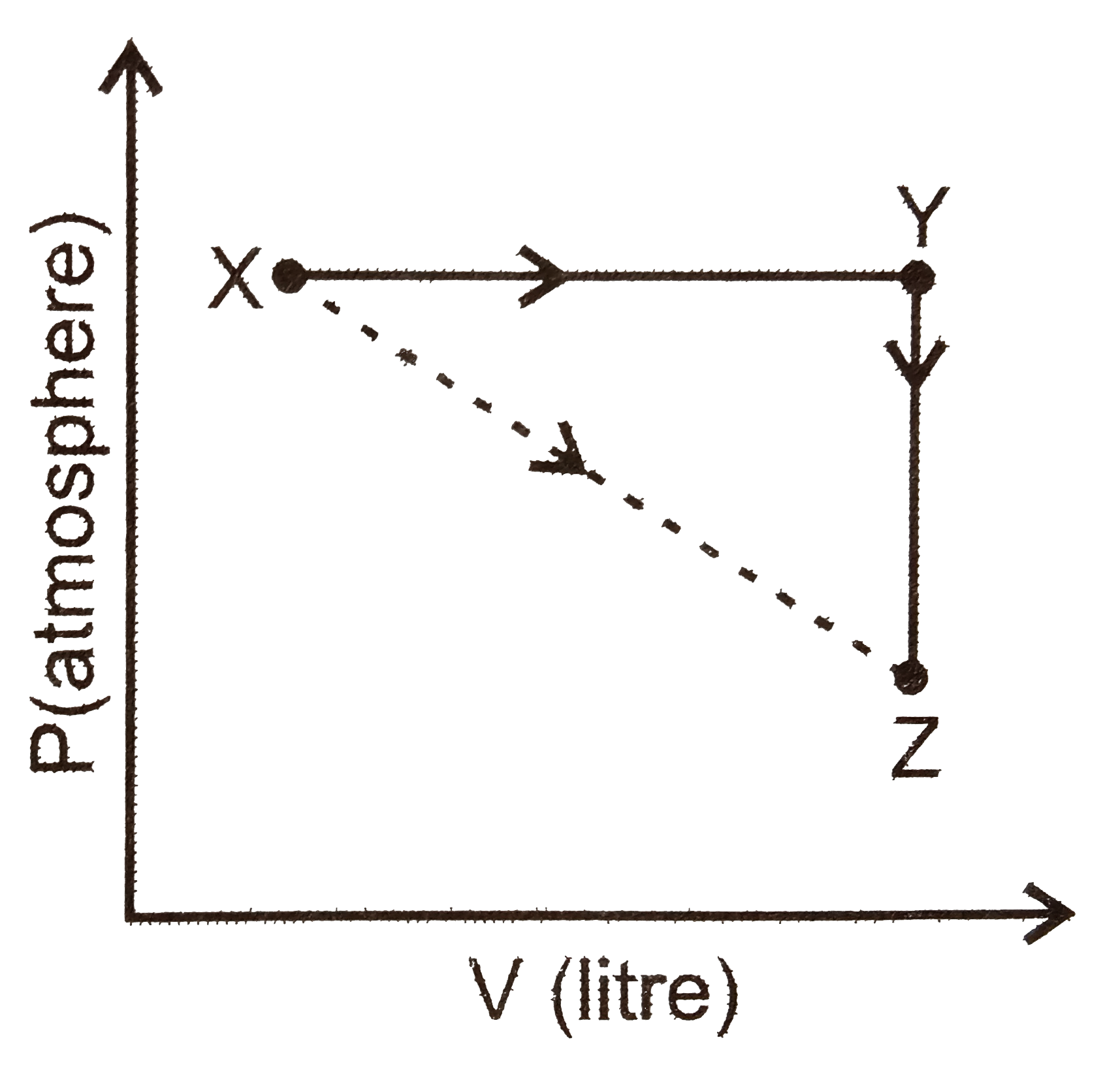
View SolutionFor an ideal gas, consider only P-V work in going from an initial state X to the final state Z. The final state Z can be reached by either of the two paths shown in the figure. Which of the following choice(s) is(are) correct? [Take ΔS as change in entropy and w as work done]

View SolutionFor an ideal gas the fractional change in its volume per degree rise in temperature at constant pressure is equal to [T is absolute temperature of gas]
View Solution

