A fixed container is fitted with a piston which is attached to a spring of spring constant k. The other and of the spring is attached to a rigid wall. Initially the spring is in its natural length and the length of container between the piston and its side wall is L. Now an dideal diatomic gas is slowly filled in the container so that the piston moves quasistatically. It pushed the piston by x so that the spring now is compressed by x. The total rotaional kinetic energy of the gas molecules in terms of the displacement x of the piston is (there is vacuum outside the container)
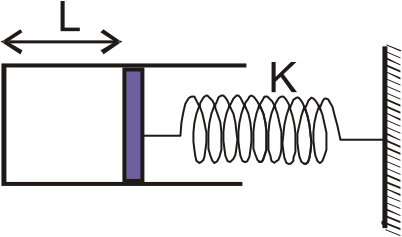
kxL
4kxL
kx(x+L)
2kx2L
Rotational K.E= Rotational degree of freedom×12nRT
2×12nRT=nRT=PV
=PA,VA= force on piston (L+X)=kx(L+x)
Topper's Solved these Questions
Similar Questions
Which of the following graph depicts spring constant k versus length l of the spring correctly
View SolutionA block of mass m is attached to a spring of force constant k whose other end is fixed to a horizontal surface. Initially the spring is in its natural length and the block is released from rest. The average force acting on the surface by the spring till the instant when the block has zero acceleration for the first time is

View SolutionA block of mass m, attached to a spring of spring constant k, oscilltes on a smooth horizontal table. The other end of the spring is fixed to a wall. If it has speed v when the spring is at its naturla lenth, how far will it move on the table before coming to an instantaneous rest?
View SolutionTwo equal masses are attached to the two ends of a spring of spring constant k. The masses are pulled out symmetrically to stretch the spring by a length x over its natural length. The work done by the spring one each mass is
View SolutionMethod 3 of W
Mass of a piston shown in Fig. is m and area of cross-section is A. Initially spring is in its natural length. Find work done by the gas.

View SolutionA block of mass m is attached with a spring in vertical plane as shown in the figure. If initially spring is in its natural length and the block is released from rest, then maximum extension in the spring will be
View Solution"A mass is attached to one end of a spring and by holding the other end in hand, the spring is whirled in a horizontal circle" What happens to the length of the spring ?
View SolutionFind the maximum tension in the spring if initially spring at its natural length when block is released from rest.

View SolutionA block of mass m, attacted to a string of spring constant k, oscillates on a smooth horizontal table. The other end of the spring is fixed to a wall. The block has a speed v when the spring is at its natural length. Before coming to an instantaneous rest. If the block moves a distance x from the mean position, then
View SolutionA block of mass 2kg is attached with a spring of spring constant 4000Nm−1 and the system is kept on smooth horizontal table. The other end of the spring is attached with a wall. Initially spring is stretched by 5cm from its natural position and the block is at rest. Now suddenly an impulse of 4kg−ms−1 is given to the block towards the wall.
Find the velocity of the block when spring acquires its natural length
View Solution
