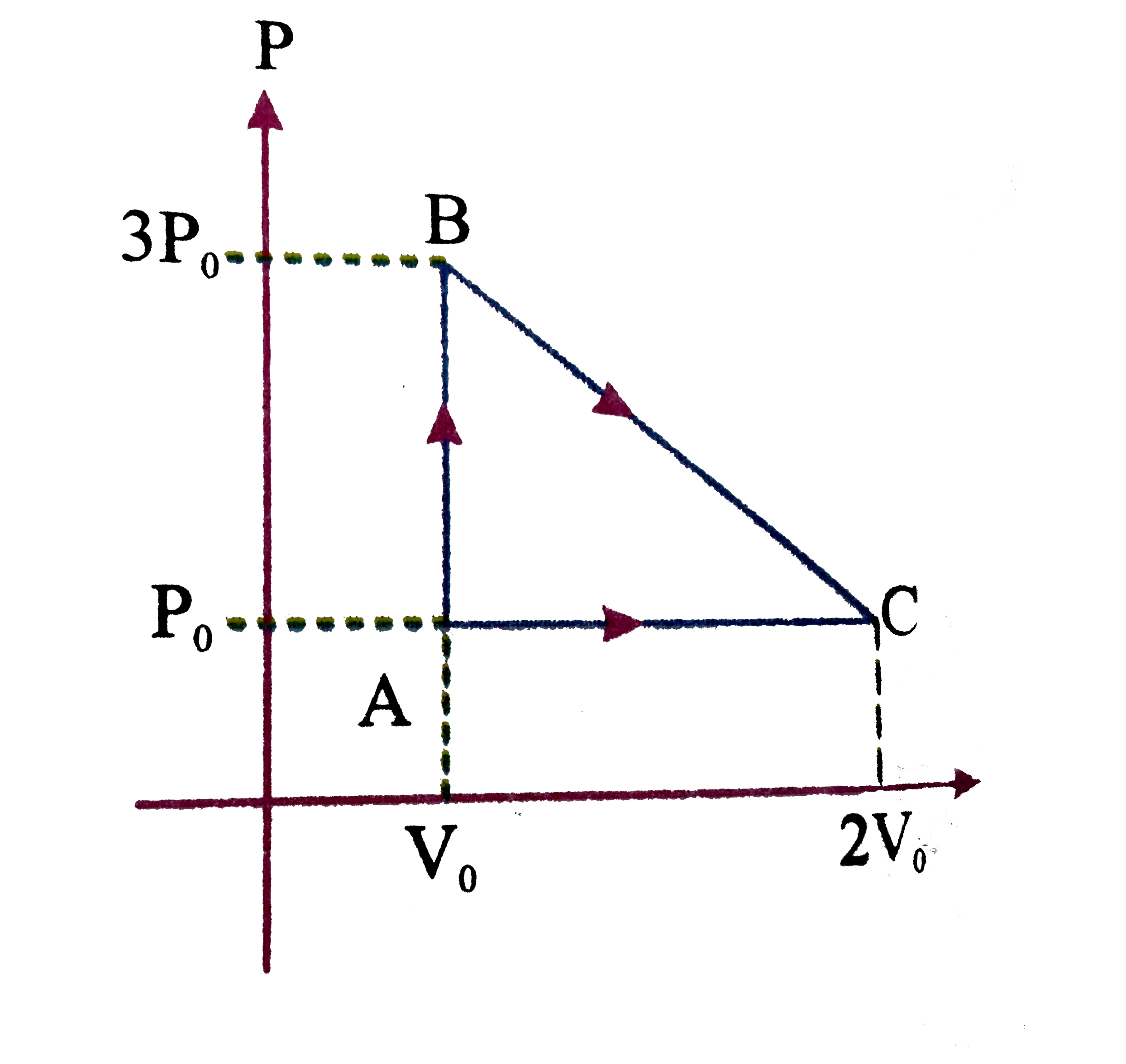
One mole of an ideal monatomic gas (intial temperature T0) is made to go through the cycle abca as shown in the figure. If U denotes the internal energy, then choose the correct alternatives
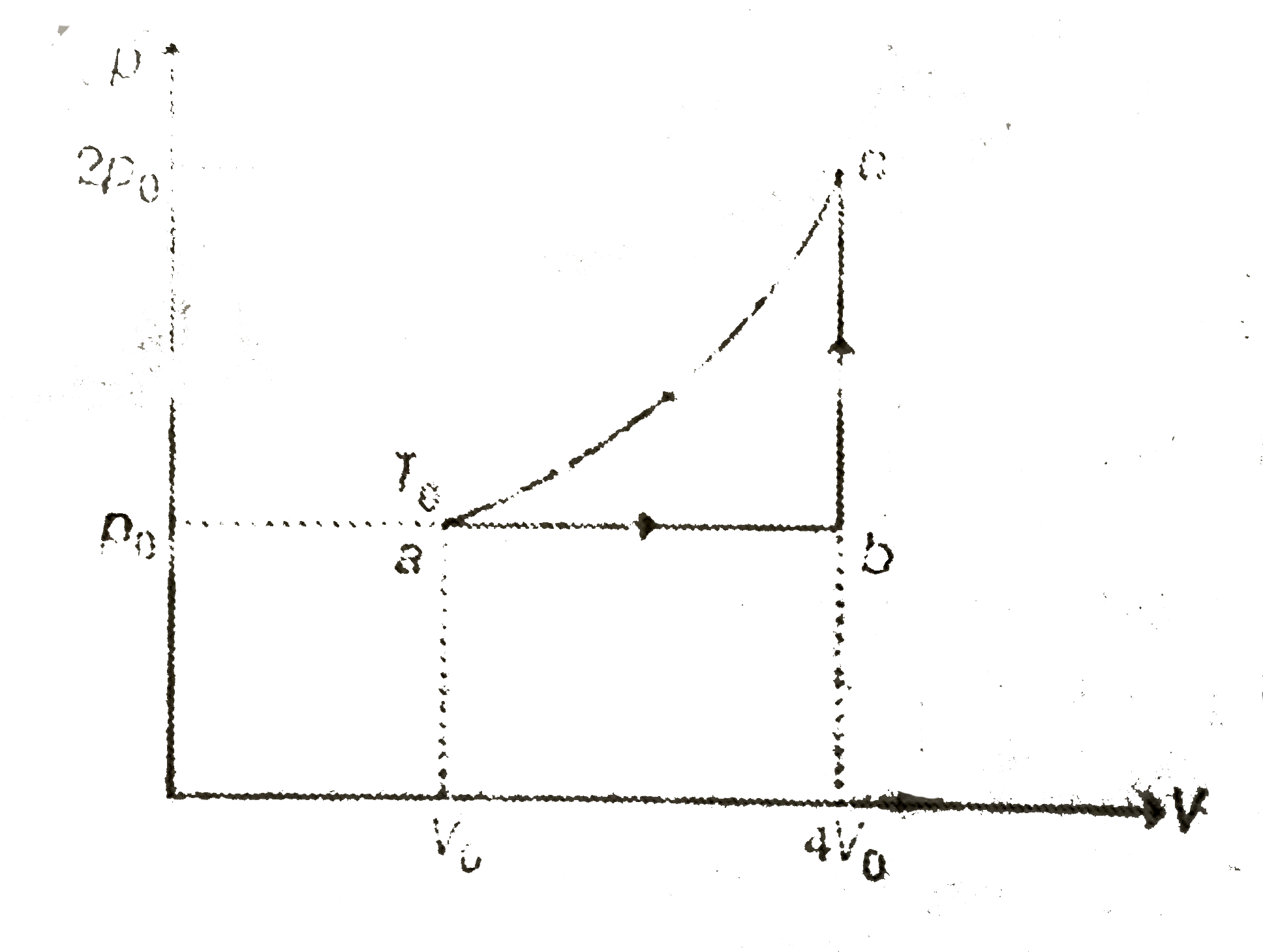
Uc−Ua=10.5RT0
Ub−Ua=+4RT0
Wc→a=−3P0V0
Uc>Ub>Ua
(a) Uc−Ua=nCvdT=(1)3R2(8T0−T0)=212RT0
(b) Ub−Ua=nCvdT
=(1)3R2(3T0−T0)=4.5RT0 (wrong)
(c) Wc→a cannot be determined, but
|Wc→a|>∣Wa→b∣
|Wc→a|>3P0V0' Hence (C) is wrong

Topper's Solved these Questions
Similar Questions
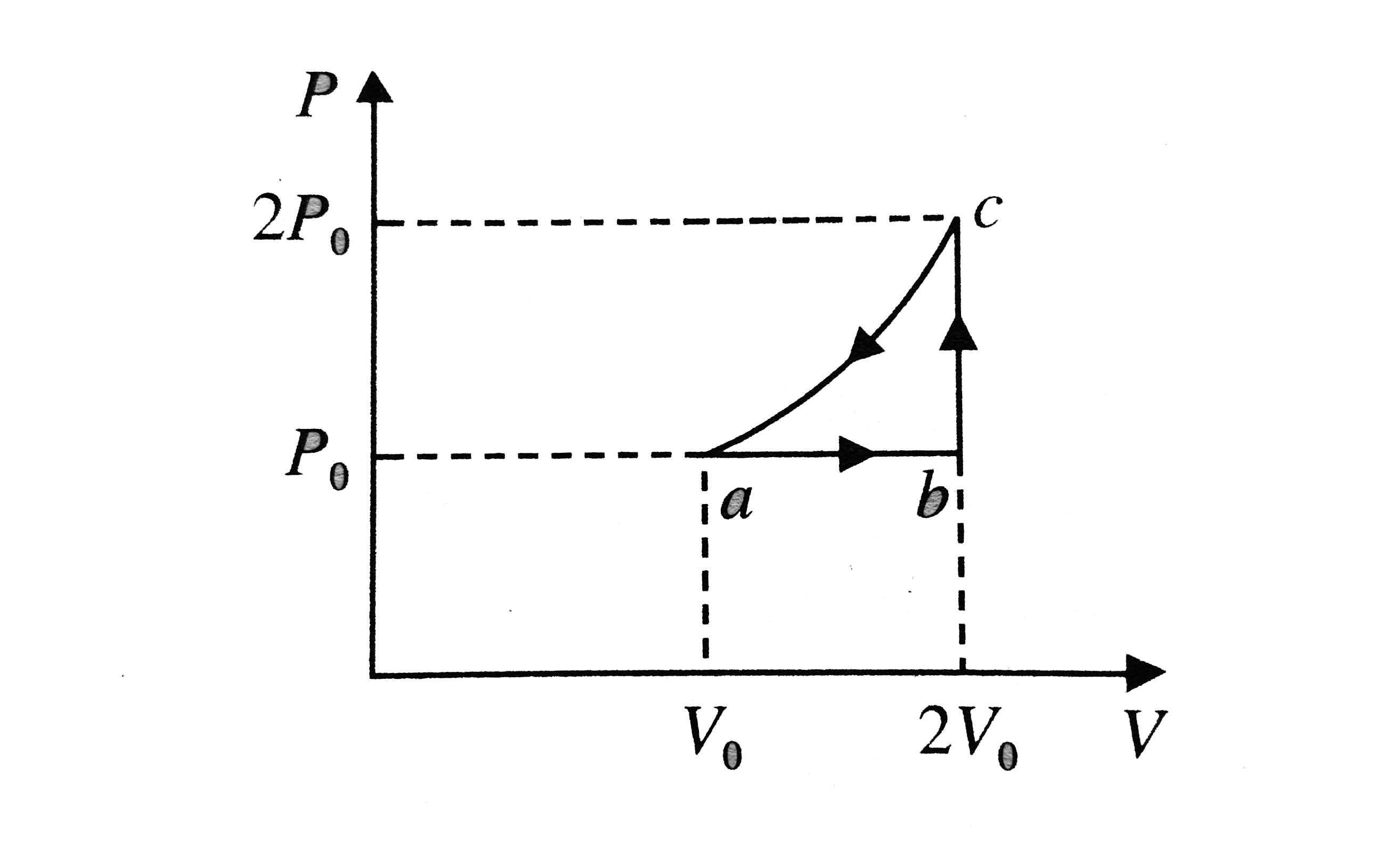
One mole of an ideal monatomic gas has initial temperature T0, is made to go through the cycle abca shown in Fig. If U denotes the internal energy, then choose the correct alternative
View SolutionOne mole of an ideal monoatomic gas is caused to go through the cycle shown in figure. Then the change in the internal energy of gas from a to b and b to c is respectively
View SolutionOne mole of an ideal mono-atomic gas is caused to go through the cycle shown in the figure below. Then the change in the internal enegry in expanding the gas from a to c along the path abc is:

View SolutionOne mole of an ideal diatomic gas undergoes a transition from A to B along a path AB as shown in the figure
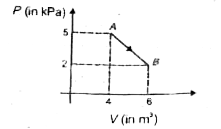
The change to internal energy of the gas during the transition is
View SolutionA sample of an ideal monoatomic gas is taken round the cycle ABCA as shown in the figure the work done during the cycle is

View SolutionOne mole of an ideal diatomic gas undergoes a transition from A to B along a path AB as shown in the figure,
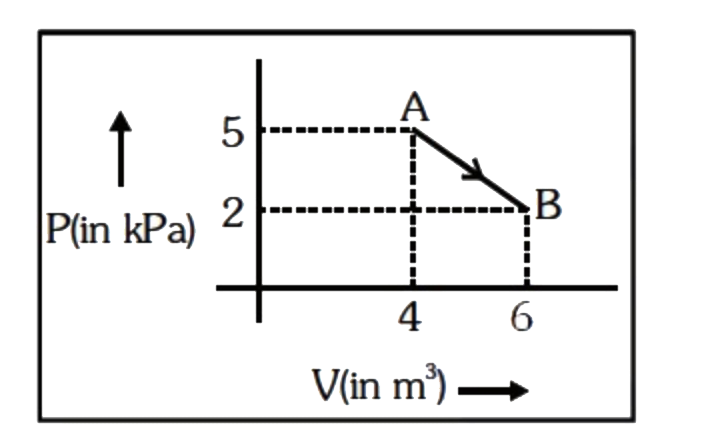
The change in internal energy of the gas during the transition is :
View SolutionOne mole of an ideal monoatomatic gas is taken round the cylic process ABCA as shown Then
View SolutionOne mole of an ideal monoatomic gas is taken at a temperature of 300K. Its volume is doubled keeping its pressure constant. Find the change in internal energy.
View SolutionOne mole of ideal monatomic gas is carried through the reversible cyclic process as shown in figure. Calculate the max temperature attained by the gas during the cycle.

View SolutionOne mole of an ideal monatomic gas at temperature T0 expands slowly according to the law P=kV (k is constant). If the final temperature is 4T0 then heat supplied to gas is
View Solution
