A block of mass 2kg is attached with a spring of spring constant 4000Nm−1 and the system is kept on smooth horizontal table. The other end of the spring is attached with a wall. Initially spring is stretched by 5cm from its natural position and the block is at rest. Now suddenly an impulse of 4kg−ms−1 is given to the block towards the wall.
Find the velocity of the block when spring acquires its natural length
(a) 5ms−1
(b) 3ms−1
(c) 6ms−1
(d) None of these
The correct Answer is:B
To solve the problem, we will follow these steps:
Step 1: Understand the given data
- Mass of the block, m=2kg
- Spring constant, k=4000N/m
- Initial stretch of the spring, xi=5cm=0.05m
- Impulse given to the block, J=4kg m/s
- Initial velocity of the block, u=0m/s (since it is at rest)
Step 2: Calculate the change in velocity due to the impulse
The impulse-momentum theorem states:
J=mΔv
Where Δv=v−u. Since the initial velocity u=0:
4=2(v−0)
v=42=2m/s
So, the velocity of the block after the impulse is v=2m/s.
Step 3: Apply the work-energy theorem
When the spring returns to its natural length, the work done by the spring will equal the change in kinetic energy of the block. The work done by the spring can be expressed as:
W=12kx2i−12kx2f
Where xf=0 (natural length of the spring). Thus:
W=12kx2i
Substituting the values:
W=12×4000×(0.05)2=12×4000×0.0025=5J
Step 4: Calculate the change in kinetic energy
The initial kinetic energy KEi when the spring is stretched is:
KEi=12mu2=12×2×02=0J
The final kinetic energy KEf when the spring reaches its natural length is:
KEf=12mv2f
Using the work-energy theorem:
W=KEf−KEi
5=12×2×v2f−0
5=v2f
vf=√5≈3.16m/s
Step 5: Conclusion
The velocity of the block when the spring acquires its natural length is approximately 3m/s.
- Mass of the block, m=2kg
- Spring constant, k=4000N/m
- Initial stretch of the spring, xi=5cm=0.05m
- Impulse given to the block, J=4kg m/s
- Initial velocity of the block, u=0m/s (since it is at rest)
The impulse-momentum theorem states:
J=mΔv
Where Δv=v−u. Since the initial velocity u=0:
4=2(v−0)
v=42=2m/s
So, the velocity of the block after the impulse is v=2m/s.
When the spring returns to its natural length, the work done by the spring will equal the change in kinetic energy of the block. The work done by the spring can be expressed as:
W=12kx2i−12kx2f
Where xf=0 (natural length of the spring). Thus:
W=12kx2i
Substituting the values:
W=12×4000×(0.05)2=12×4000×0.0025=5J
The initial kinetic energy KEi when the spring is stretched is:
KEi=12mu2=12×2×02=0J
The final kinetic energy KEf when the spring reaches its natural length is:
KEf=12mv2f
Using the work-energy theorem:
W=KEf−KEi
5=12×2×v2f−0
5=v2f
vf=√5≈3.16m/s
The velocity of the block when the spring acquires its natural length is approximately 3m/s.
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Comprehension Based Questions
3 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective
21 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 More Than One Correct
8 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Medical entrances s gallery
19 Videos
Similar Questions
A block of mass 2kg is attached with a spring of spring constant 4000Nm−1 and the system is kept on smooth horizontal table. The other end of the spring is attached with a wall. Initially spring is stretched by 5cm from its natural position and the block is at rest. Now suddenly an impulse of 4kg−ms−1 is given to the block towards the wall.
Approximate distance travelled by the block when it comes to rest for a second time (not including the initial one) will be (Take √45=6.70)
View SolutionA block of mass 2kg is attached with a spring of spring constant 4000Nm−1 and the system is kept on smooth horizontal table. The other end of the spring is attached with a wall. Initially spring is stretched by 5cm from its natural position and the block is at rest. Now suddenly an impulse of 4kg−ms−1 is given to the block towards the wall.
Approximate distance travelled by the block when it comes to rest for a second time (not including the initial one) will be (Take √45=6.70)
View SolutionA block of mass m, attached to a spring of spring constant k, oscilltes on a smooth horizontal table. The other end of the spring is fixed to a wall. If it has speed v when the spring is at its naturla lenth, how far will it move on the table before coming to an instantaneous rest?
View SolutionA block of mass m, attacted to a string of spring constant k, oscillates on a smooth horizontal table. The other end of the spring is fixed to a wall. The block has a speed v when the spring is at its natural length. Before coming to an instantaneous rest. If the block moves a distance x from the mean position, then
View Solutiona block of mass 0.1 kg attached to a spring of spring constant400Nm pulled horizontally from x=0 tox1=10mm. Find the work done by the spring force
View SolutionA block of mass 0.1 kg attached to a spring of spring constant 400 N/m is putted rightward from x0=0 to x1=15 mm. Find the work done by spring force.
View SolutionA block attached with an ideal spring is kept on a smooth horizontal surface. Now the free end of the spring is pulled with a constant velocity u horizontally. Then the maximum energy stored in the spring and bock system during subsequent motion is :
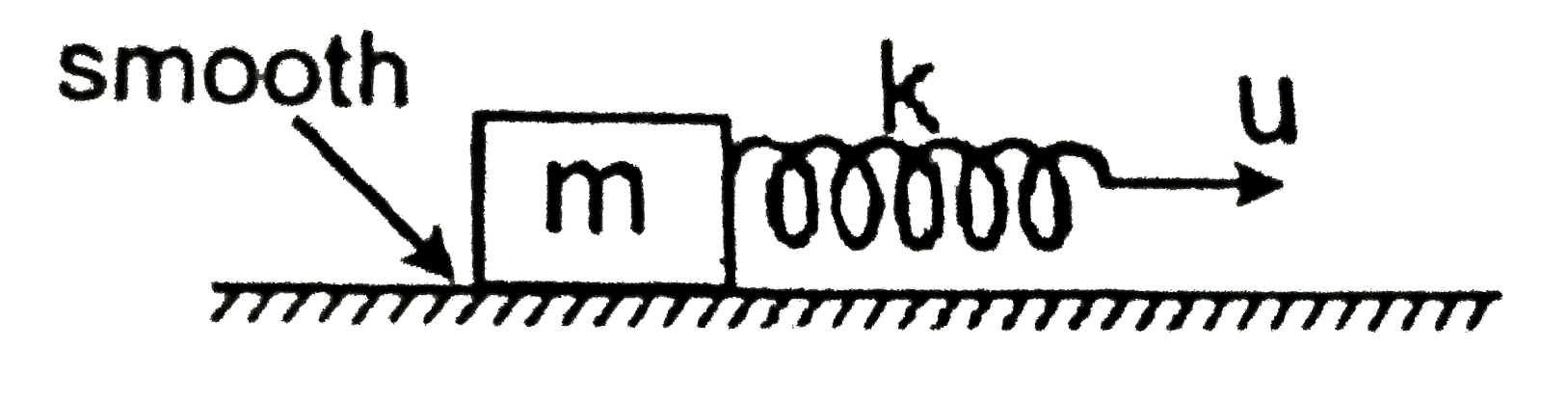
View SolutionA block of mass m is connected to another block of mass M by a massless spring of spring constant k. the blocks are kept of a smooth horizontal plane and are at rest. The spring is unstretched when a constant force F starts acting on the block of mass M of pull it. Find the maximum extension of the spring

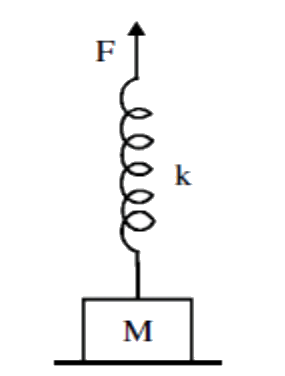
View SolutionA block of mass m is kept on a rough horizontal surface and is attached with a massless spring of force constant k. The minimum constant force applied on the other end of the spring of lift the block is
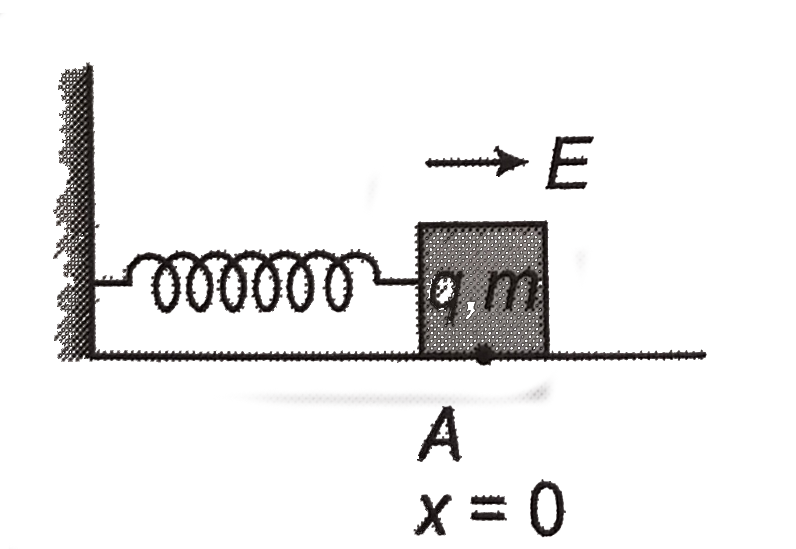
View SolutionA block of mass m having charge q is attached to a spring of spring constant k. This arrangement is placed in uniform electric field E on smooth horizontal surface as shown in the figure. Initially spring in unstretched. Find the extension of spring in equilibrium position and maximum extension of spring.
View Solution
