A block of mass m, attached to a spring of spring constant k, oscilltes on a smooth horizontal table. The other end of the spring is fixed to a wall. If it has speed v when the spring is at its naturla lenth, how far will it move on the table before coming to an instantaneous rest?
To solve the problem step by step, let's analyze the situation involving the block, spring, and the conservation of energy.
Step 1: Understand the initial conditions
- The block of mass m is attached to a spring with spring constant k.
- The spring is at its natural length when the block has a speed v.
- The table is smooth, meaning there is no friction acting on the block.
Hint: Identify the initial state of the system where the spring is unstretched, and the block is moving with speed v.
Step 2: Apply the conservation of mechanical energy
Since there are no non-conservative forces acting on the system (like friction), the mechanical energy is conserved. The total mechanical energy at the initial state (when the spring is at its natural length) is equal to the total mechanical energy at the final state (when the block comes to instantaneous rest).
Hint: Write down the equation for conservation of energy: initial potential energy + initial kinetic energy = final potential energy + final kinetic energy.
Step 3: Write the energy equations
- Initial kinetic energy when the spring is at its natural length:
KEi=12mv2
- Initial potential energy when the spring is at its natural length:
PEi=0(since the spring is unstretched)
- Final kinetic energy when the block comes to rest:
KEf=0
- Final potential energy when the spring is stretched by a distance x:
PEf=12kx2
Hint: Set up the equation: KEi+PEi=KEf+PEf.
Step 4: Substitute the energy values into the equation
Substituting the values we have:
12mv2+0=0+12kx2
Hint: Simplify the equation by eliminating the zero terms.
Step 5: Rearrange the equation
This simplifies to:
12mv2=12kx2
Multiplying both sides by 2 to eliminate the fractions:
mv2=kx2
Hint: Isolate x2 on one side of the equation.
Step 6: Solve for x
Rearranging gives:
x2=mv2k
Taking the square root of both sides:
x=v√mk
Hint: Remember that x represents the distance the block moves before coming to rest.
Final Answer
The distance x that the block will move on the table before coming to instantaneous rest is:
x=v√mk
- The block of mass m is attached to a spring with spring constant k.
- The spring is at its natural length when the block has a speed v.
- The table is smooth, meaning there is no friction acting on the block.
Since there are no non-conservative forces acting on the system (like friction), the mechanical energy is conserved. The total mechanical energy at the initial state (when the spring is at its natural length) is equal to the total mechanical energy at the final state (when the block comes to instantaneous rest).
- Initial kinetic energy when the spring is at its natural length:
KEi=12mv2
- Initial potential energy when the spring is at its natural length:
PEi=0(since the spring is unstretched)
- Final kinetic energy when the block comes to rest:
KEf=0
- Final potential energy when the spring is stretched by a distance x:
PEf=12kx2
Substituting the values we have:
12mv2+0=0+12kx2
This simplifies to:
12mv2=12kx2
Multiplying both sides by 2 to eliminate the fractions:
mv2=kx2
Rearranging gives:
x2=mv2k
Taking the square root of both sides:
x=v√mk
The distance x that the block will move on the table before coming to instantaneous rest is:
x=v√mk
Topper's Solved these Questions
- WORK AND ENERGYBook:HC VERMA ENGLISHChapter:WORK AND ENERGYExercise:Worked out Examples
Explore 14 Videos
- WORK AND ENERGYBook:HC VERMA ENGLISHChapter:WORK AND ENERGYExercise:Objective -1
Explore 10 Videos
- WAVE MOTION AND WAVES ON A STRINGBook:HC VERMA ENGLISHChapter:WAVE MOTION AND WAVES ON A STRINGExercise:Question for short Answer
Explore 7 Videos
Similar Questions
A block of mass m, attacted to a string of spring constant k, oscillates on a smooth horizontal table. The other end of the spring is fixed to a wall. The block has a speed v when the spring is at its natural length. Before coming to an instantaneous rest. If the block moves a distance x from the mean position, then
View SolutionA block of mass 2kg is attached with a spring of spring constant 4000Nm−1 and the system is kept on smooth horizontal table. The other end of the spring is attached with a wall. Initially spring is stretched by 5cm from its natural position and the block is at rest. Now suddenly an impulse of 4kg−ms−1 is given to the block towards the wall.
Approximate distance travelled by the block when it comes to rest for a second time (not including the initial one) will be (Take √45=6.70)
View SolutionA block of mass 2kg is attached with a spring of spring constant 4000Nm−1 and the system is kept on smooth horizontal table. The other end of the spring is attached with a wall. Initially spring is stretched by 5cm from its natural position and the block is at rest. Now suddenly an impulse of 4kg−ms−1 is given to the block towards the wall.
Approximate distance travelled by the block when it comes to rest for a second time (not including the initial one) will be (Take √45=6.70)
View SolutionA block of mass 2kg is attached with a spring of spring constant 4000Nm−1 and the system is kept on smooth horizontal table. The other end of the spring is attached with a wall. Initially spring is stretched by 5cm from its natural position and the block is at rest. Now suddenly an impulse of 4kg−ms−1 is given to the block towards the wall.
Find the velocity of the block when spring acquires its natural length
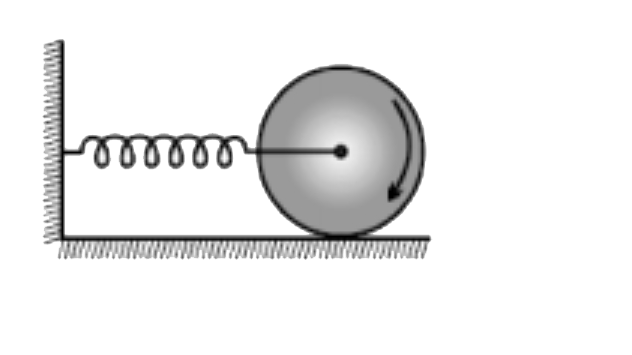
View SolutionA disc of mass M and radius R has a spring of constant k attached to its center , the other end of the spring being fixed to a vertical wall. If the disk rolls without slipping on a level floor, how far to the right does the centre of mass move , if Initially the spring was unstretched and the angular speed of the disc was ω0
View SolutionA block of mass m is attached to a spring of force constant k whose other end is fixed to a horizontal surface. Initially the spring is in its natural length and the block is released from rest. The average force acting on the surface by the spring till the instant when the block has zero acceleration for the first time is
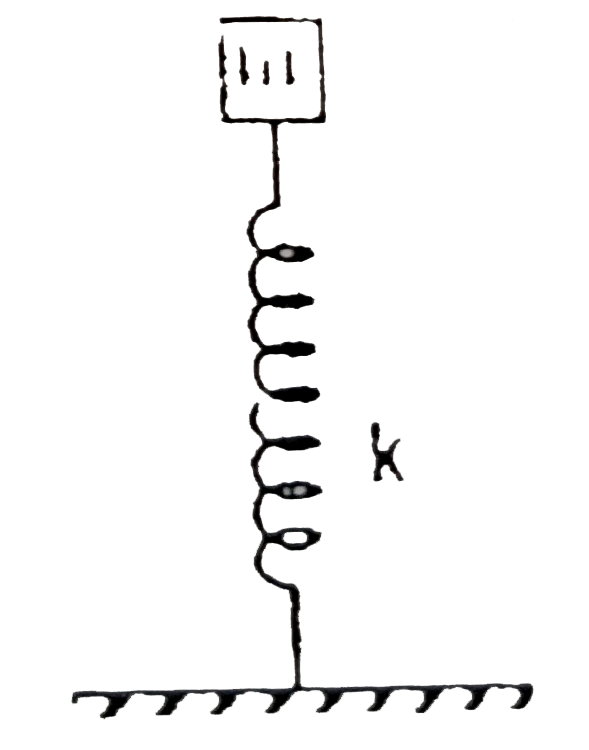
View SolutionA ball of mass m is attached to the lower end of a light vertical spring of force constant K. The upper end of the spring is fixed. The ball is released from rest with the spring at its normal ( unstretched ) length, and comed to rest again after descending through a distance x.
View Solution"A mass is attached to one end of a spring and by holding the other end in hand, the spring is whirled in a horizontal circle" What happens to the length of the spring ?
View SolutionA block of mass m is attached to one end of a mass less spring of spring constant k. the other end of spring is fixed to a wall the block can move on a horizontal rough surface. The coefficient of friction between the block and the surface is μ then the compession of the spring for which maximum extension of the spring becomes half of maximum compression is .
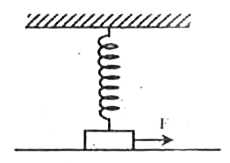
View SolutionA spring is attached with a block of mass m and a fixed horizontal roof as shown. The block is lying on a smooth horizontal table and initially the spring is vertical and unstretched. Natural length of spring is 3l0. A constant horizontal force F is applied on the block so that block moves in the direction of force. When length of the spring becomes 5l0, block leaves contact with the table. Find the constant force F, if initial and final velocity of block is zero.
View Solution

