Figure shown a block P of mass m resting on a smooth horizontal surface, attached to a spring of force constant k which is rigidly fixed on the wall on left side, shown in the figure . At a distance l to the right of the block there is a rigid wall. If block is pushed towards left so that spring is compressed by a distance 5l/3 and when released, if will starts its oscillations. If collision of block with the wall is considered to be perfectly elastic. Find the time period of oscillation of the block.

As shown in figure , as the block its released from rest at a distance 5/3 from its mean position, this will be the amplitude of oscillation. But on the other side of mean position block can move only up to a distance l from mean position and then it will return from this point with equal velocity due to elastic collision . Consider figure . If no right wall is present during oscillation, block P will excute complete SHM on right side of mean position also up t its amplitude 5l/3 . Thus, we can observe the block P at a point X at distance l from mean position (where in our case wall is present) . if block passes this position at speed v (which is the speed with , which block bites the wall in our case) after reaching its exterme position y, it willl return and during return path it will cross the position X with the same speed v (as displacement from mean position is same).

Thus, we can state that in our case of given problem , that block P is executing SHm but it skips a XYX on right half of its motion due to electric collision of the block with the wall. if T0 is the time period of this oscillation we look at figure which shown the corresponding circular motion repersantation. Here during oscillation of point P partical P0 covers its circular motion along ECDAF, and from F it instantly jumps to E (due to elastic collision of P with wall at X) and again carry out ECDAF and so on thus we can find the time of this total motion as

t=π+2θω=π+2sin−1(3/5)√km
=√mk[π+2sin−1(32)]
We can also find the time period of this motion by sub-tracting the time FYE from the total time period as
t=2π−2cos−1(35)ω
=√mk[π+2cos1(35)]
Equations (i) and (ii) will result same numerical value.
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Exercise 4.1
23 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Exercise 4.2
23 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Single correct anwer type
14 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
Similar Questions
A block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. The maximum compression in spring is

View SolutionA bullet of mass m embeds itself in a block of mass M resting on a smooth horizontal surface, attached to a spring of force constant k. If the initial speed of the bullet is v0 along horizontal, find (a) the maximum compression of the spring and (b) the time for the bullet - block system to come to rest.
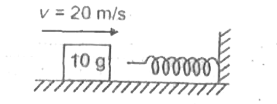
View SolutionA block of 10 g slides on smooth horizontal surface with 20 m/s towards a spring of spring constant 100 N/m placed horizontally (as shown in figure). The maximum compression in spring is
View SolutionA block of mass m, lying on a smooth horizontal surface, is attached to a spring (of negligible mass) of spring constant k. The other end of the spring is fixed, as shown in the figure. The block is initally at rest in its equilibrium position. If now the block is pulled withe a constant force F, the maximum speed of the block is :

View SolutionIn the figure, the block of mass m, attached to the spring of stiffness k is in correct with the completely elastic wall, and the compression in the spring is e. The spring is compressed further by e by displacing the block towards left and is then released. If the collision between the block and the wall is completely eleastic then the time period of oscillation of the block will be

View SolutionAs shown in figure, the left block rests on a table at distance l from the edge while the right block is kept at the same level so that thread is unstrectched and does not sah and then released. What will happen first?
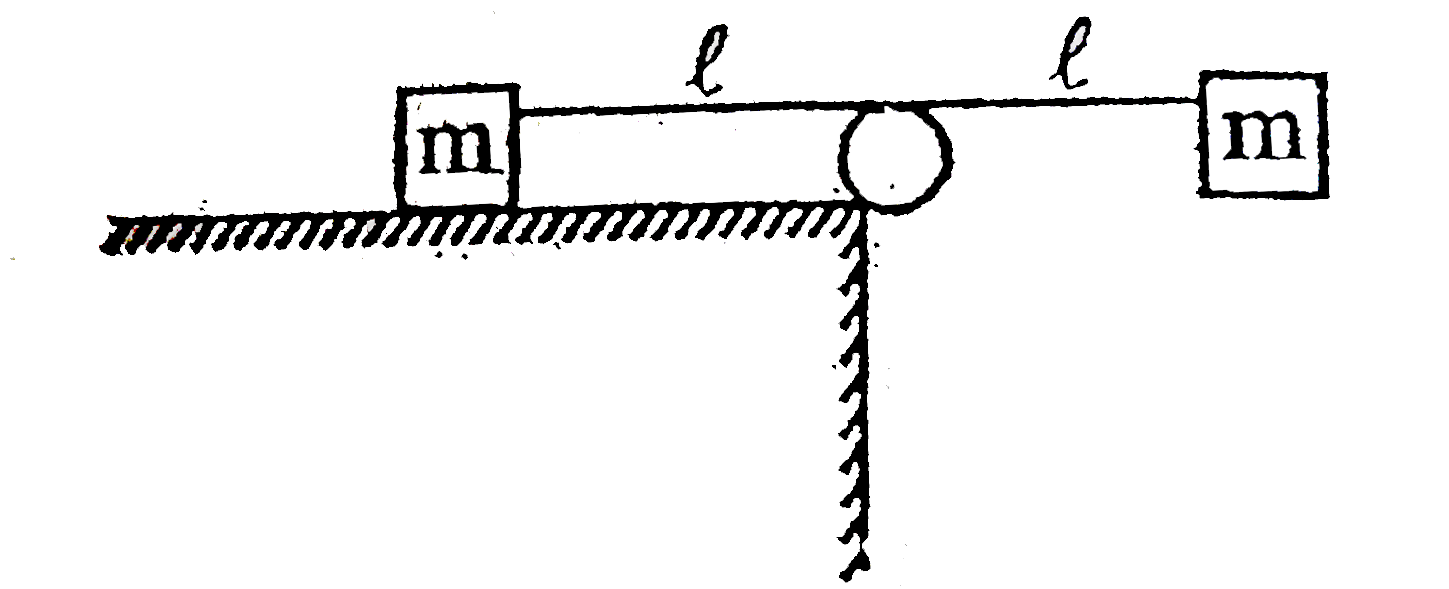
View SolutionA block of mass m held touching the upper end of a light spring of force constant K as shown in figure. Find the maximum potential energy stored in the spring if the block is released suddenly on the spring.

View SolutionA block of mass m sliding n a smooth horizontal surface with velocity →v meets a long horizontal spring fixed ast one end and having spring constant k as shown n figure. Find the maximum compression of the spring. Will the velocity of the block be the same as v whenit comes back to the original position shown?

View SolutionA block of mass m compresses a spring iof stifffness k through a distacne l/2 as shown in the figure .If the block is not fixed to the spring the period of motion of the block is

View SolutionFigure shown a block P of mass m resting on a smooth floor at a distance l from a regid wall. Block is pushed towards right by a distance 3/2 and released. When block passes from its mean position another block of mass m1 so that the combined block just collides with the left wall.

View Solution
