A bullet of mass m embeds itself in a block of mass M resting on a smooth horizontal surface, attached to a spring of force constant k. If the initial speed of the bullet is v0 along horizontal, find (a) the maximum compression of the spring and (b) the time for the bullet - block system to come to rest.
To solve the problem step by step, we will break it down into two parts: finding the maximum compression of the spring and calculating the time for the bullet-block system to come to rest.
Part (a): Maximum Compression of the Spring
1. Conservation of Momentum:
When the bullet of mass m embeds itself into the block of mass M, we can use the conservation of momentum to find the velocity v of the bullet-block system immediately after the collision.
Initial momentum=Final momentum
mv0=(M+m)v
Rearranging gives:
v=mv0M+m
2. Kinetic Energy of the System:
The kinetic energy of the bullet-block system right after the collision is given by:
KE=12(M+m)v2
Substituting the expression for v:
KE=12(M+m)(mv0M+m)2=12m2v20M+m
3. Work Done by the Spring:
The work done on the spring when it is compressed by a distance x is given by:
W=12kx2
Setting the kinetic energy equal to the work done by the spring:
12kx2=12m2v20M+m
Canceling the 12 from both sides:
kx2=m2v20M+m
4. Solving for Maximum Compression x:
Rearranging gives:
x2=m2v20k(M+m)
Taking the square root:
x=mv0√k(M+m)
Part (b): Time for the Bullet-Block System to Come to Rest
1. Simple Harmonic Motion (SHM):
After the maximum compression, the bullet-block system will start oscillating back and forth due to the spring. The system will undergo SHM with angular frequency ω:
ω=√kM+m
2. Time to Come to Rest:
In SHM, the time taken to go from maximum compression to the point where the velocity is zero (the equilibrium position) is a quarter of the period T:
T=2πω=2π√M+mk
Therefore, the time to come to rest (from maximum compression to equilibrium) is:
t=T4=π2√M+mk
Final Answers:
(a) The maximum compression of the spring is:
x=mv0√k(M+m)
(b) The time for the bullet-block system to come to rest is:
t=π2√M+mk
When the bullet of mass m embeds itself into the block of mass M, we can use the conservation of momentum to find the velocity v of the bullet-block system immediately after the collision.
Initial momentum=Final momentum
mv0=(M+m)v
Rearranging gives:
v=mv0M+m
The kinetic energy of the bullet-block system right after the collision is given by:
KE=12(M+m)v2
Substituting the expression for v:
KE=12(M+m)(mv0M+m)2=12m2v20M+m
The work done on the spring when it is compressed by a distance x is given by:
W=12kx2
Setting the kinetic energy equal to the work done by the spring:
12kx2=12m2v20M+m
Canceling the 12 from both sides:
kx2=m2v20M+m
Rearranging gives:
x2=m2v20k(M+m)
Taking the square root:
x=mv0√k(M+m)
After the maximum compression, the bullet-block system will start oscillating back and forth due to the spring. The system will undergo SHM with angular frequency ω:
ω=√kM+m
In SHM, the time taken to go from maximum compression to the point where the velocity is zero (the equilibrium position) is a quarter of the period T:
T=2πω=2π√M+mk
Therefore, the time to come to rest (from maximum compression to equilibrium) is:
t=T4=π2√M+mk
(a) The maximum compression of the spring is:
x=mv0√k(M+m)
t=π2√M+mk
Topper's Solved these Questions
- OSCILLATIONSBook:AAKASH INSTITUTE ENGLISHChapter:OSCILLATIONSExercise:ASSIGNMENT ( SECTION-J )
Explore 8 Videos
- OSCILLATIONSBook:AAKASH INSTITUTE ENGLISHChapter:OSCILLATIONSExercise:EXAMPLE
Explore 21 Videos
- OSCILLATIONSBook:AAKASH INSTITUTE ENGLISHChapter:OSCILLATIONSExercise:ASSIGNMENT ( SECTION-H ( MULTIPLE TRUE-FALSE TYPE QUESTIONS) )
Explore 3 Videos
- NUCLEIBook:AAKASH INSTITUTE ENGLISHChapter:NUCLEIExercise:ASSIGNMENT (SECTION-D)
Explore 10 Videos
- PHYSICAL WORLDBook:AAKASH INSTITUTE ENGLISHChapter:PHYSICAL WORLDExercise:ASSIGNMENT (Section-B)
Explore 4 Videos
Similar Questions
A bullet of mass m leaves a gun of mass M kept on a smooth horizontal surface . If the speed of the bullet relative to the gun is v , the magnitude of recoil speed of the gun will be
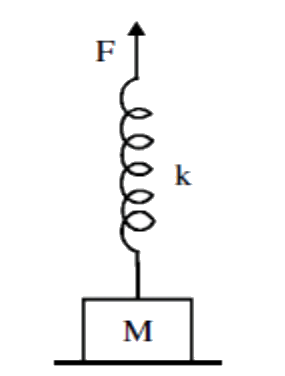
View SolutionA block of mass m is kept on a rough horizontal surface and is attached with a massless spring of force constant k. The minimum constant force applied on the other end of the spring of lift the block is
View SolutionA block of mass m is placed at rest on a smooth wedge of mass M placed at rest on a smooth horizontal surface. As the system is released

View SolutionA block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. The maximum compression in spring is

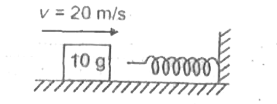
View SolutionA block of 10 g slides on smooth horizontal surface with 20 m/s towards a spring of spring constant 100 N/m placed horizontally (as shown in figure). The maximum compression in spring is
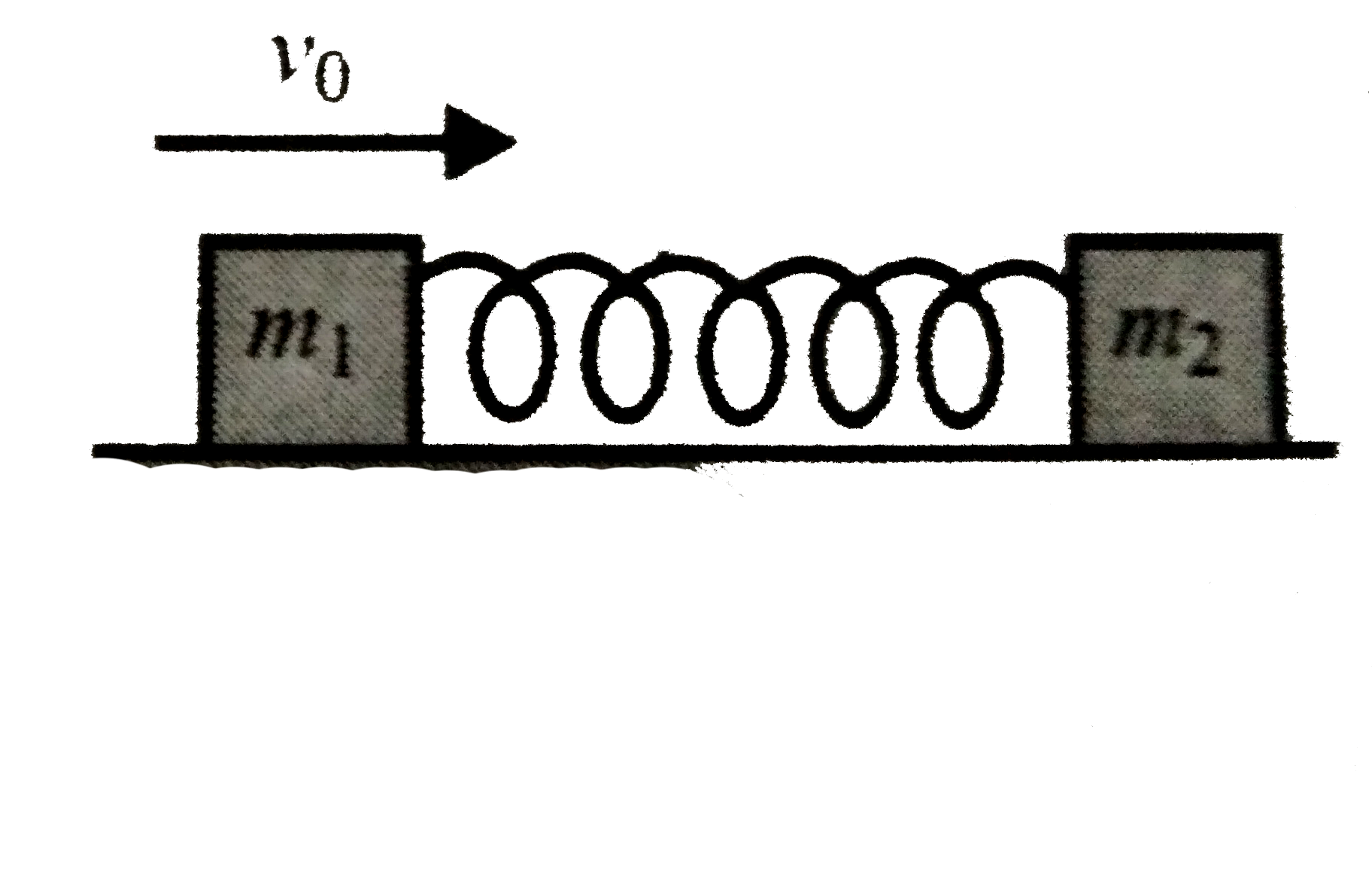
View SolutionTwo smooth blocks of mases m1andm2 attached with an ideal spring of stiffness k and kept on hrozontal surface. If m1 is projected with a horizontal velocity v0. Find the maximum compression of the spring.
View SolutionA block of mass m is moving with an initial velocity v0 towards a stationary spring of stiffness k attached to the wall as shown in figure

a. Find the maximum compression in the spring.
b. Is the work done by the spring negative or positive?
View SolutionA block of mass m sliding n a smooth horizontal surface with velocity →v meets a long horizontal spring fixed ast one end and having spring constant k as shown n figure. Find the maximum compression of the spring. Will the velocity of the block be the same as v whenit comes back to the original position shown?

View SolutionTwo blocks A and B of mass 16kg and 64kg are placed on a smooth horizontal surface. Blocks are connected by a spring of spring constant 100N/m. Find the ratio of maximum speed of block A to maximum speed of block B.

View SolutionA block of mass m, lying on a smooth horizontal surface, is attached to a spring (of negligible mass) of spring constant k. The other end of the spring is fixed, as shown in the figure. The block is initally at rest in its equilibrium position. If now the block is pulled withe a constant force F, the maximum speed of the block is :

View Solution

