As a result of adding two mutually perpendicular oscillations of equal frequency the motion of an object occurs alongan ellipse, in one case the motion is clockwise, while in the other it is counter clockwise . Write the equations of motion along each coordinate axis, assuming that the initial phase along the x-axis is zero.
To solve the problem, we need to derive the equations of motion for two mutually perpendicular oscillations of equal frequency, resulting in elliptical motion. We will assume that the initial phase along the x-axis is zero.
Step 1: Define the Oscillations
We have two oscillations along the x-axis and y-axis. Let:
- The amplitude of the oscillation along the x-axis be A.
- The amplitude of the oscillation along the y-axis be B.
- The angular frequency for both oscillations be ω.
Step 2: Write the Equations of Motion
1. For the x-axis, since the initial phase is zero, the equation of motion can be written as:
x(t)=Asin(ωt)
2. For the y-axis, we need to consider two cases: one for clockwise motion and the other for counterclockwise motion.
Case 1: Clockwise Motion
In the case of clockwise motion, the equation for the y-axis can be represented as:
y(t)=Bsin(ωt+π2)
This can be simplified using the sine addition formula:
y(t)=Bcos(ωt)
Case 2: Counterclockwise Motion
In the case of counterclockwise motion, the equation for the y-axis can be represented as:
y(t)=Bsin(ωt−π2)
This can also be simplified:
y(t)=−Bcos(ωt)
Step 3: Final Equations
Thus, the final equations of motion for both cases are:
- Clockwise Motion:
x(t)=Asin(ωt)
y(t)=Bcos(ωt)
- Counterclockwise Motion:
x(t)=Asin(ωt)
y(t)=−Bcos(ωt)
Summary
The equations of motion for the object moving in an elliptical path due to the superposition of two perpendicular oscillations of equal frequency are derived for both clockwise and counterclockwise motions.
We have two oscillations along the x-axis and y-axis. Let:
- The amplitude of the oscillation along the x-axis be A.
- The amplitude of the oscillation along the y-axis be B.
- The angular frequency for both oscillations be ω.
1. For the x-axis, since the initial phase is zero, the equation of motion can be written as:
x(t)=Asin(ωt)
In the case of clockwise motion, the equation for the y-axis can be represented as:
y(t)=Bsin(ωt+π2)
This can be simplified using the sine addition formula:
y(t)=Bcos(ωt)
In the case of counterclockwise motion, the equation for the y-axis can be represented as:
y(t)=Bsin(ωt−π2)
This can also be simplified:
y(t)=−Bcos(ωt)
Thus, the final equations of motion for both cases are:
- Clockwise Motion:
x(t)=Asin(ωt)
y(t)=Bcos(ωt)
x(t)=Asin(ωt)
y(t)=−Bcos(ωt)
The equations of motion for the object moving in an elliptical path due to the superposition of two perpendicular oscillations of equal frequency are derived for both clockwise and counterclockwise motions.
Topper's Solved these Questions
- OSCILLATIONSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - OSCILLATIONSEXERCISE - EXAMPLE
21 Videos
- OSCILLATIONSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - OSCILLATIONSEXERCISE - Exercise
18 Videos
- OSCILLATIONSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - OSCILLATIONSEXERCISE - ASSIGNMENT ( SECTION-I(SUBJECTIVE TYPE QUESTIONS) )
7 Videos
- NUCLEIBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - NUCLEIEXERCISE - ASSIGNMENT (SECTION-D)
10 Videos
- PHYSICAL WORLDBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - PHYSICAL WORLDEXERCISE - ASSIGNMENT (Section-B)
4 Videos
Similar Questions
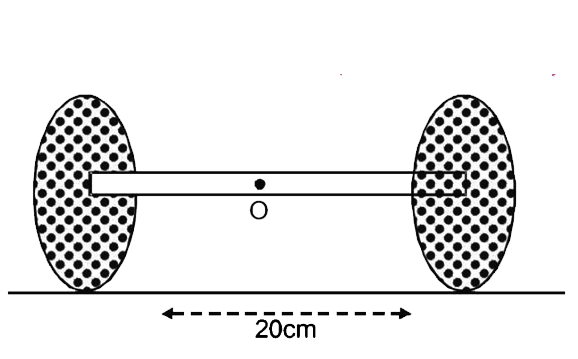
Two thin circular disks of mass 2kg and radius 10 cm each are joined by a rigid massless rod of length 20 cm. the axis of the rod is along the perpendicular to the planes of the disk through their centres. This object is kept on a truck in such a way that the axis of the object is horizontal and perpendicular to the direction of the motion of the truck. Its friction with the floor of the truck is large enough so that the object can roll on the truck without slipping. Take x axis as the direction of motion of the truck and z-axis as the vertically upwards direction. if the truck has an acceleration of 9m/s2 Calculate:
(i) The force fo friction on each disk,
(ii) The magnitude and the direction of the frictional torque acting on each disk about the centre of mass O of the object. Express the torque in the vector form in terms of unit vectors ˆi,ˆjandˆk in the x,y, and z directions.
View SolutionTwo boats A and B moved away from a buoy anchored in the middle of a river along the mutually perpendicular straight lines. A moved along the river and B at fight angle to it Having moves off equal distances from the boy, the boats returned. Find the ratio of the times of motion of the boats, if the velocity of each boat with respect to still water in η=1.2 times greater than the velocity of water current.
View SolutionTwo simple harmonic motions with the same frequency act on a particle at right angles i.e., along X-axis and Y-axis. If the two amplitudes are equal and the phase difference is π/2, the resultant motion will be
View SolutionTwo circular coils mounted parallel to each other on the same axis carry steady currents. If an observer between the coils reports. that one coil is carrying a clockwise current i1 While the other is carrying a counter - clockwise current i2 then the two coils experience
View SolutionTwo linear simple harmonic motions of equal amplitude and frequency are impressed on a particle along x and y axis respectively. The initial phase difference between them is π2. The resultant path followed by the particle is
View SolutionA particle is subjected to two simple harmonic motions, one along the X-axis and the other on a line making an angle of 45∘ with the X-axis. The two motions are given by
x=x0sinωt and s=s0sinωt.
find the amplitude of the resultant motion.
View SolutionTwo particles execute simple harmonic motion of the same amplitude and frequency along close parallel lines. They pass each other moving in opposite directions each time their displacement is half their amplitude. Their phase difference is
View SolutionTwo short dipoles, each of diple moment p , are placed at origin. The dipole moment of one dipole is along x-axis, while that of other is along y-axis . The electric field at a point (a,0) is given by
View Solutionx=x1+x2 (where x1=4cosωt and x2=3sinωt) is the equation of motion of a particle along x-axis. The phase different between x1 and x is
View SolutionTwo wires carrying equal currents i each, are placed
perpendicular to each other, just avoiding a contact. If
one wire is held fixed and the other is free to move under
magnetic forces, what kind of motion wil results?
View Solution
