Two thin circular disks of mass 2kg and radius 10 cm each are joined by a rigid massless rod of length 20 cm. the axis of the rod is along the perpendicular to the planes of the disk through their centres. This object is kept on a truck in such a way that the axis of the object is horizontal and perpendicular to the direction of the motion of the truck. Its friction with the floor of the truck is large enough so that the object can roll on the truck without slipping. Take x axis as the direction of motion of the truck and z-axis as the vertically upwards direction. if the truck has an acceleration of $9 m / s^{2}$ Calculate:
(i) The force fo friction on each disk,
(ii) The magnitude and the direction of the frictional torque acting on each disk about the centre of mass O of the object. Express the torque in the vector form in terms of unit vectors $ˆ i, ˆ j and ˆ k$ in the x,y, and z directions.

Video Solution

Text Solution

Verified by Experts

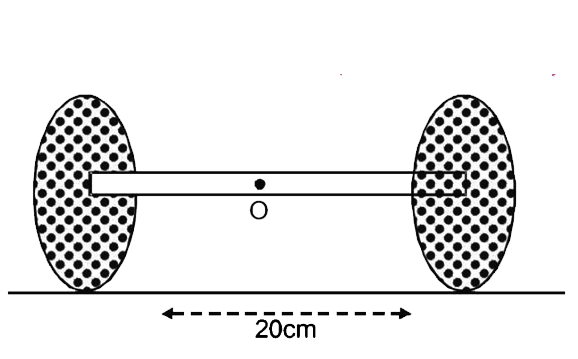
a. $F B D$ of the object with respect to truck

In the reference frame of truck it experiences a pseudoforce
$\to F = - 2 m a ˆ i$
where $a =$ acceleration of the truck.
Pseudoforce does not provide torque about the centre of the disc. Because of this force, object has tendency to side along $- v e$ $x$ -axis. Hence frictional force will act along $+ v e$ $x$ -axis.
For translational motion
$2 m a - f = 2 m a'$ ..........i
Here a'=acceleratioin of the centre of mass of the object.
For rotational motion $fR = I α$
for on slipping $α = a \frac{'}{R}$
Hence $f . R = 2 (\frac{m R^{2}}{2}) (\frac{a'}{R})$
$\Rightarrow a' = \frac{f}{m}$ .........ii
From eqn i and ii we get $f = \frac{2}{3} m a ˆ i$
Therefore force of friction on each disc is
$\frac{f}{2} = \frac{m a}{ˆ i} = 6 ˆ i$

b. ${\to f}_{1} = \frac{m a}{3} ˆ i$
${\to r}_{1} = - l ˆ j - R ˆ k \Rightarrow τ_{(f_{1})} = {\to r}_{1} \times {\to f}_{1}$
$= - (l ˆ j + R ˆ k) \times \frac{m a}{3} ˆ i$
$- \frac{m a R}{3} ˆ j + \frac{m a l}{3} ˆ k$
$= 6 \times 0.1 ˆ j + 6 \times 0.1 ˆ k$
$= - 0.6 ˆ j + 0.6 ˆ k$
$τ_{(f_{2})} = - 0.6 ˆ j - 0.6 ˆ j k$
c. Maximum value of frictional force is $2 μ m g$
$\Rightarrow \frac{2}{3} m \leq 2 μ m g \Rightarrow \geq \frac{a}{3 g}$

Updated on:21/07/2023

Two thin discs each of mass M and radius r metre are attached to form a rigid body as shown in figure. The rotational inertia of this body about an axis perpendicular to the plane of disc B and passing through its centre is

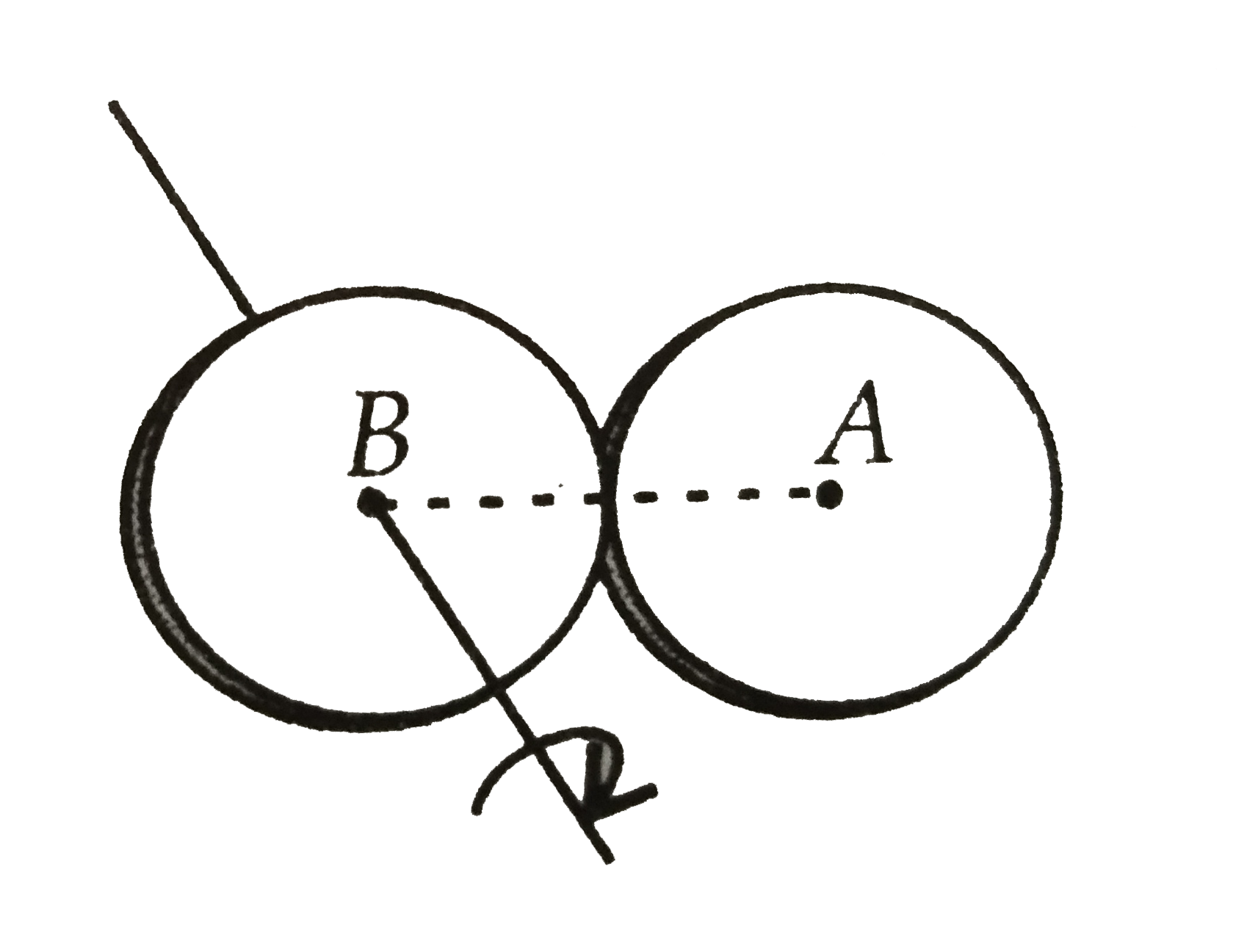A $2 M r^{2}$
B $3 M r^{2}$
C $4 M r^{2}$
D $5 M r^{2}$
Two masses each of mass $M$ are attached to the end of a rigid massless rod of length $L$ . The moment of interia of the system about an axis passing centre of mass and perpendicular to its length is.
A $M L^{2}$ /4
B $M L^{2}$ /2
C $M L^{2}$
D $2 M L^{2}$
The radius of gyration of an uniform rod of length $l$ about an axis passing through one of its ends and perpendicular to its length is.
A $\frac{l}{\sqrt{2}}$
B $\frac{l}{3}$
C $\frac{l}{\sqrt{3}}$
D $\frac{l}{2}$