A circular disc of mass M1 and radius R, initially moving, With a constant angular speed ω is gently placed coaxially on a stationary circular disc of mass M2 and radius R, as shown in Fig. There is a frictional force between the two discs.
If disc M2 is placed on a smooth surface, then 'determine' the final angular speed of each disc.
b. Determine the work done by friction.
c. Determine the fractional loss in kinetic energy. i.e. △K/Ki
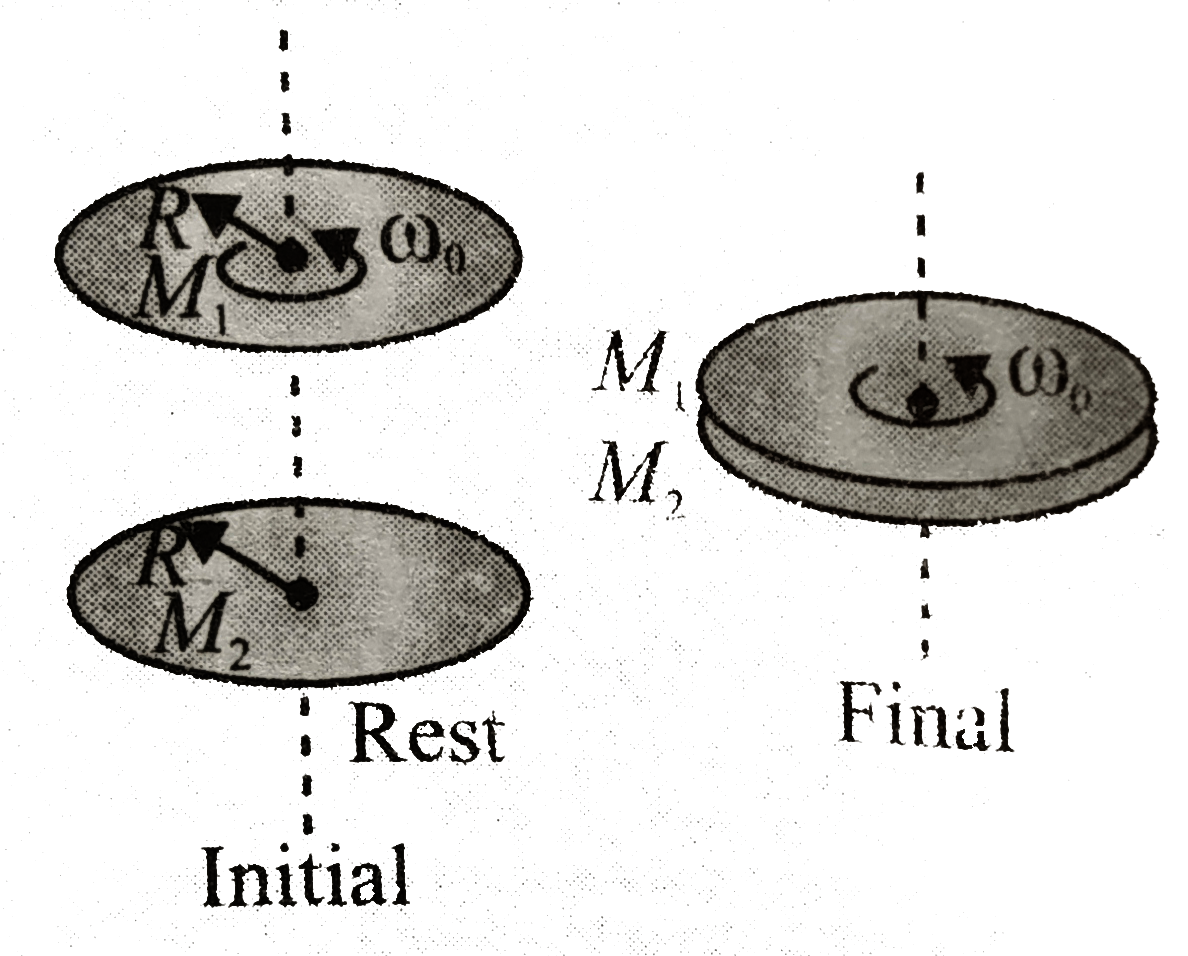
The frictional force between the two discs exerts a retarding torque on M1 and an accelerating torque on M2. Till both the discs start moving together with a common angular speed ω, the angular momentum of each disc changes but the angular momentum o the whole system (M1+M2) remains conserved as there is no torque acint on the system.
A rotating disc is gently placed on a momentum, we get
Li=Lf
(M1R22)ω0=(M1R22+M2R22)ω
ω=M1ω0M1+M2
b. The work done by frictioln done by friction is equal to te change in kinetic energy of the system.
Wf=Kf−Ki
Ki=12I1ω20=12(M1R22)ω20=14M1R2ω20
Kf=12(I1+I2)ω2=12(M1+M2)R22[M1ω0M1+M2]2
=14M21(M1+M2)R2ω22
Wf=Kf−Ki=−14(M1+M2M1+M2)R2ω20
Note that the negative sign shows that work done by friction reduces the kinetic energy of the system.
c. The fractional loss in kinetic energy is
△KKi=M2M1+M2
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.321videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.413videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.111videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer11videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer16videos
SOUND WAVES AND DOPPLER EFFECT
Similar Questions
A disc of mass m and radius R rotating with angular speed ω0 is placed on a rough surface (co-officient of friction =μ). Then
 View Solution
View SolutionA disc of mass M and Radius R is rolling with an angular speed ω on the horizontal plane. The magnitude of angular momentum of the disc about origin is:
View SolutionA circular disc of mass 2 kg and radius 10 cm rolls without slipping with a speed 2 m/s. The total kinetic energy of disc is
View SolutionA force F acts tangentially on a part of a uniform disc of mass 'm' and radius 'R' hinged at point O. The force exerted by hinge on the portion of disc initially.
 View Solution
View SolutionA circular disc of mass M and radius R rotating with speed of ω and another disc of same mass M and radius R/2 placed co axially on first disc, after sometime disc-2 also attain constant speed w2 . Find loss of percentage in energy
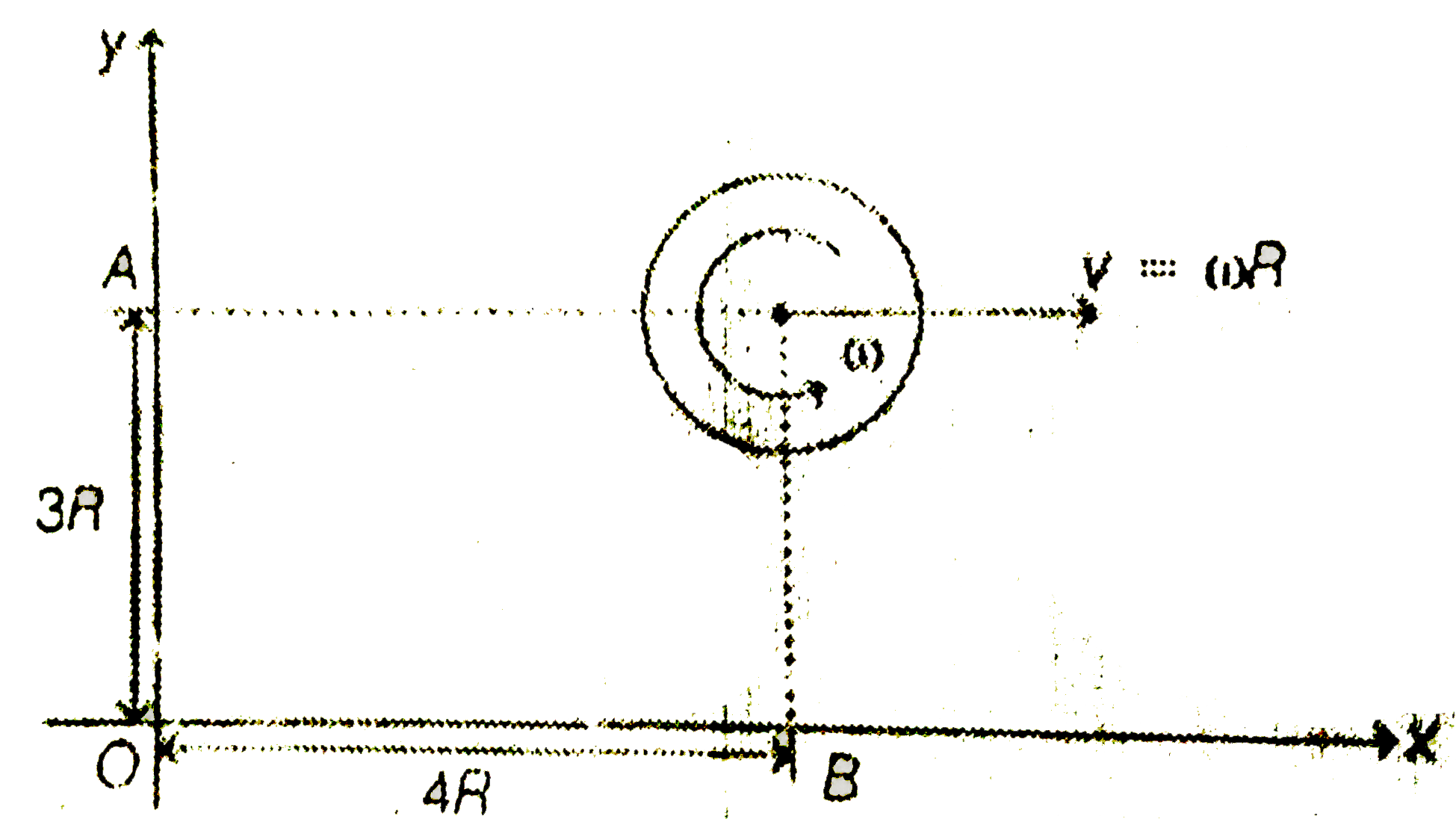
View SolutionA disc of mass m and radius R moves in the x−y plane as shown in Fig. The angular momentum of the disc about the origin O at the instant shown is
 View Solution
View SolutionA disc of mass M and radius R moves in the x-y plane as shown in the figure. The angular momentum of the disc at tihe instant shows is
 View Solution
View SolutionA circular hole of radius R/2 is cut from a circular disc of radius R. The disc lies in the xy-plane and its centre coincides with the origin. If the remaining mass of the disc is M, then
a. determine the initial mass of the disc and
b. determine its moment of inertia about the z-axis.
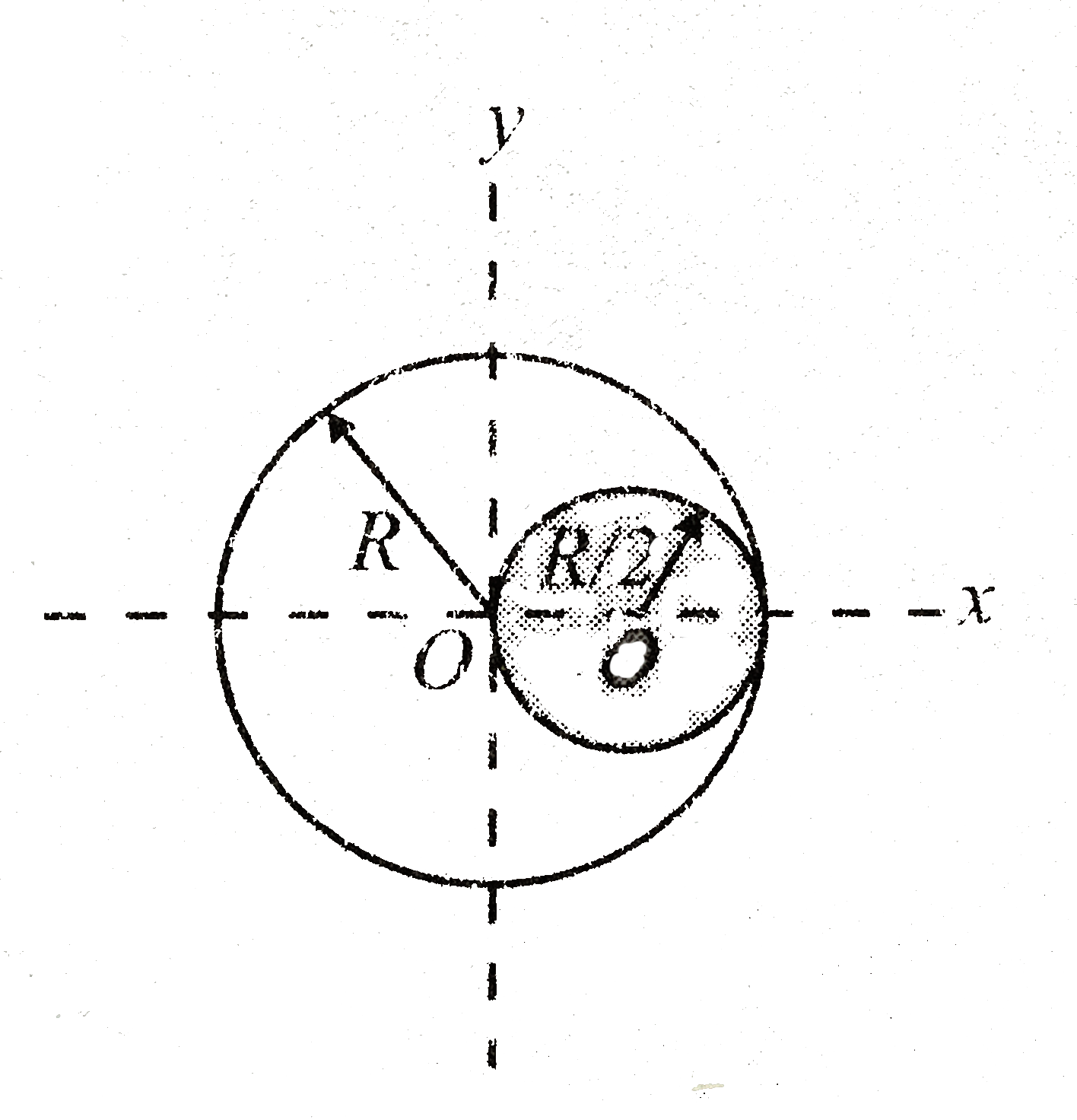 View Solution
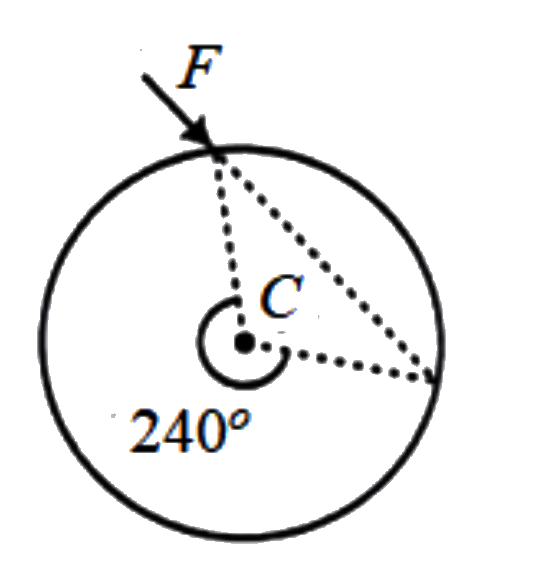
View SolutionA uniform disc of mass M and radius R is hinged at its centre C . A force F is applied on the disc as shown . At this instant , angular acceleration of the disc is
 View Solution
View SolutionInitial angular velocity of a circular disc of mass M is ω1. Then two small spheres of mass m are attached gently to two diametrically opposite points on the edge of the disc. What is the final angular velocity of the disc -
View Solution
