A sphere rolling on a horizontal rough surface Collides elastically with a smooth vertical wall, as shown in Fig. State which of the following statements is true or false.
 a. After collision, the velocity of the centre of mass gets reversed.
a. After collision, the velocity of the centre of mass gets reversed.
b. Angular momentum of the sphere about the point of contact with the wall is conserved.
c. Angular momentum of the sphere about a stationary point on the horizontal surface is conserved.
d. Just after collision the point of contact with the horizontal surface is moving towards the wall.
e. After collision the friction force acts on the sphere such that it decreases the linear speed and increases the angular speed.
f. Finally, when the sphere starts rolling, it is moving away from the wall.
a. True: collision is elastic and the friction impulse is not generated.
b. True: The net impulse passes through the point of contact with the wall. Therefore,angular impulse about the point of contact with the wall is zero and hence the angular momentum is conserved.
c. False: Angular momentum is not conserved because the net impulse exerts torque about a stationary point on the floor.
d.False: The point of contact with the horizontal surface moves away from the wall.
e. False: Friction fore decreases both the speeds.
f. True: Wen the sphere starts rolling, it is moving away from the wall because the angular velocityy becomes zero before the linear velocity. The linear acceleration of the CM of the sphere is
a=−μg
The angular acceleration about the CM is
α=−52μgR
The negative sign shows that both the acceleration have the retarding effect. The time after which the linear velocity will become zero is
t1=vμg

and the time after which the angular velocity will become zero is
t2=25ωRμg=25vμgh (∴v=ωR)
Note that t2<t1

Topper's Solved these Questions
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Subjective
19 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Single Correct
142 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.3
21 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
Similar Questions
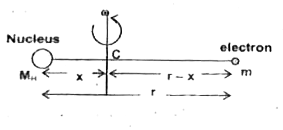
The angular momentum of the atom about the centre of mass will be
View SolutionA sphere rolling on a horizontal rough surface collides elastically with a smooth vertical wall, as shown in figure. During collision, angular momentum of the sphere is conserved about ____________. (Any point O on the surface/point of contact P)

View SolutionA thin ring of mass m and radius R is in pure rolling over a horizontal surface. If v0 is the velocity of the centre of mass of the ring, then the angular momentum of the ring about the point of contact is
View SolutionA sphere moving with a velocity v0 on a smooth surface suddenly enters on a rough horizontal surface as shown in Fig. State which of the following statements are true or false
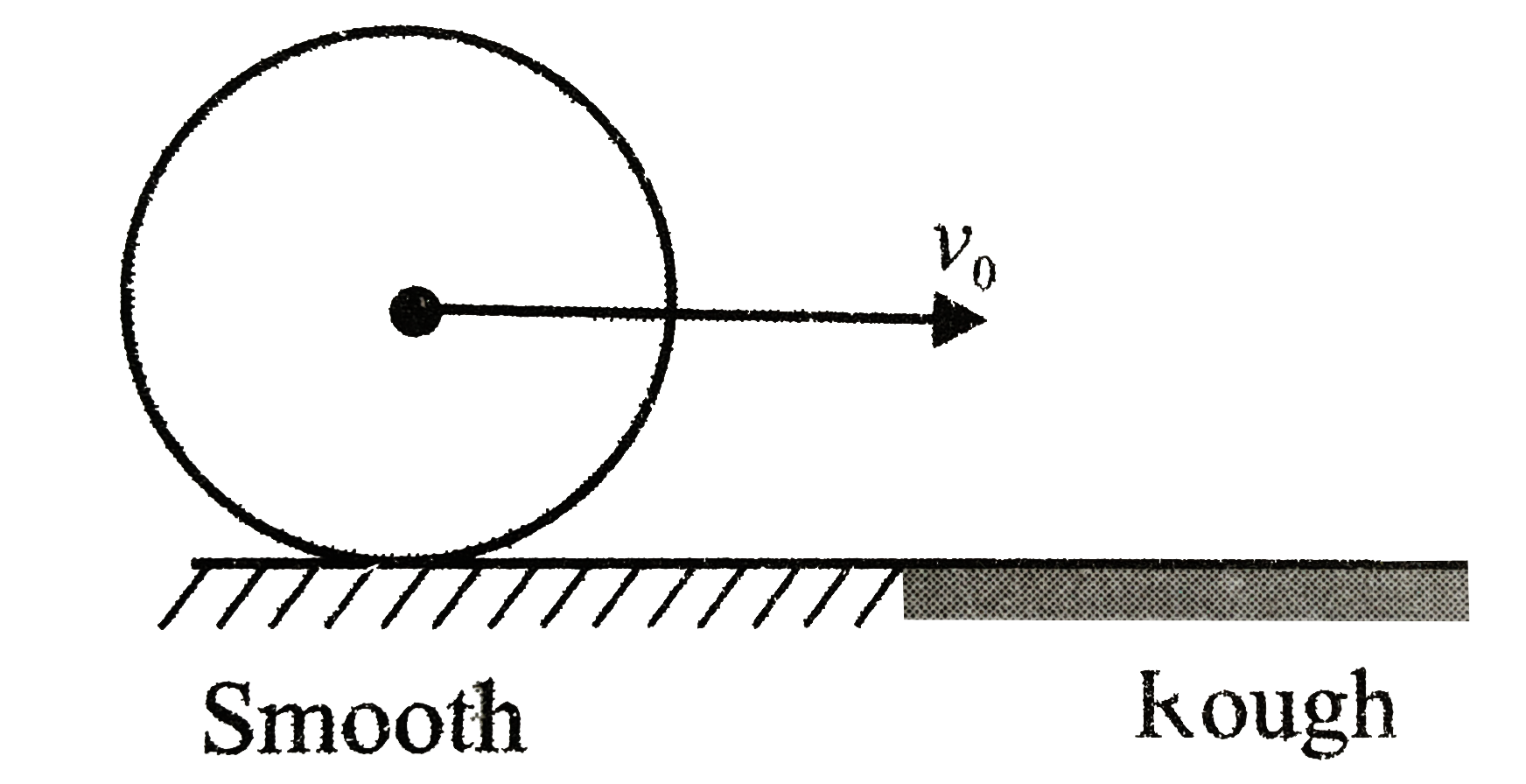
a. The sphere loses translational kinetic energy and gains rotational kinetic energy.
b. The total energy of the sphere is conserved.
c. The angular momentum of the sphere about any point OD the surface is conserved.
d. The final velocity attained by the centre of mass is 2v0/3.
View SolutionA solid sphere rolling on a rough horizontl surface with a lilner speed v collides elastically with a fixed, smooth, vertical wall. Find the speed of the sphere after it has started pure rolling in the backward direction.
View SolutionA ball, rolling purely on a horizontal floor with centre's speed v, hits a smooth vertical wall surface elastically. Answer the following questions.

Just after the collision is over, the velocity of the lowest point of the ball is
View SolutionA sphere rolls on a horizontal surface. Is there any point of the sphere which has a vertical velocity?
View SolutionA sphere of mass M rolls without slipping on rough surface with centre of mass has constant speed v0. If its radius is R, then the angular momentum of the sphere about the point of contact is.
View SolutionA sphere of mass M rolls without slipping on rough surface with centre of mass has constant speed v0. If mass of the sphere is m and its radius be R, then the angular momentum of the sphere about the point of contact is.
View SolutionA metal sphere is hung by a string fixed to a wall. The forces acting on the sphere are shown in fig Which of the following statements are correct?
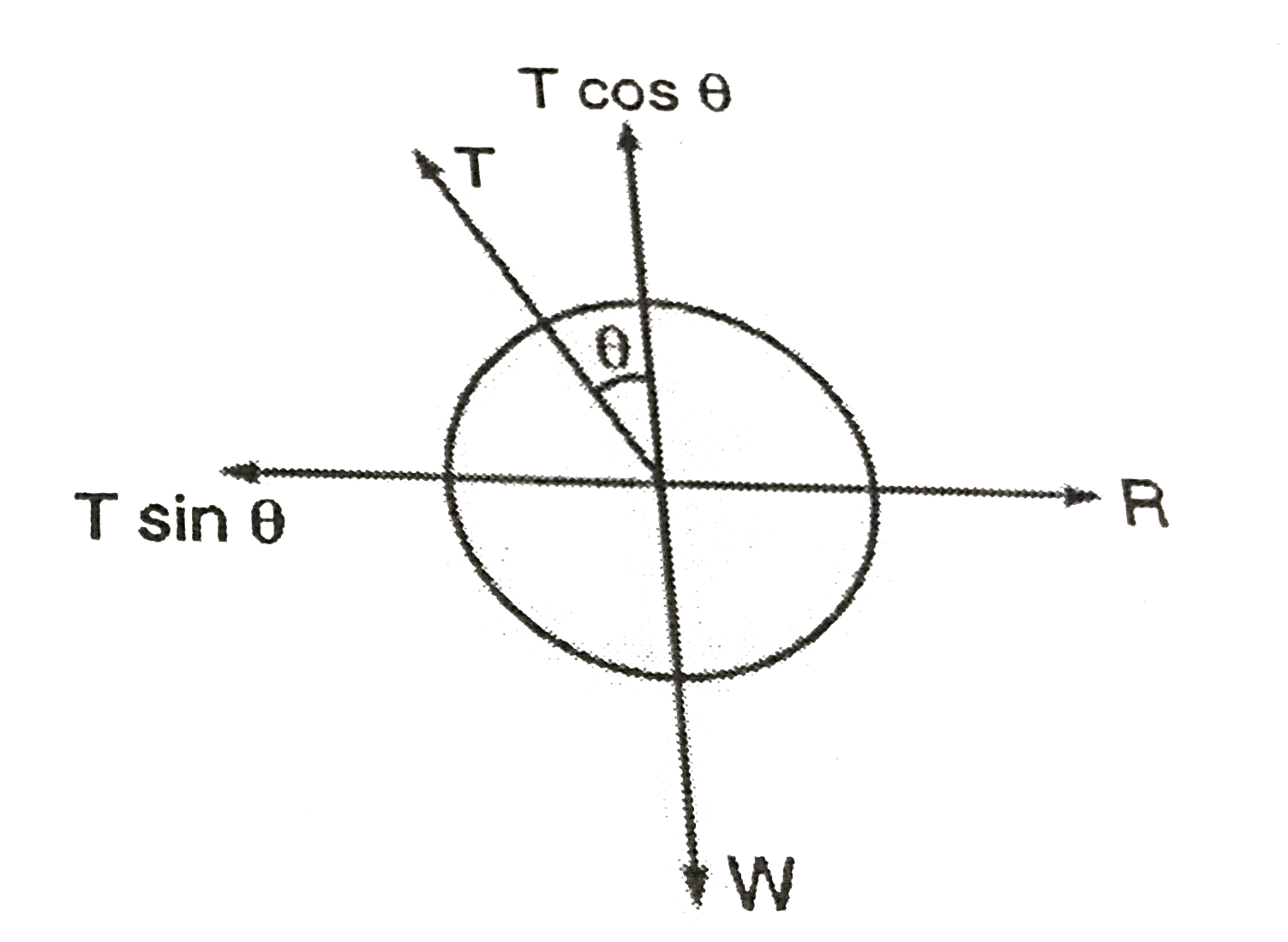
View Solution