A ball, rolling purely on a horizontal floor with centre's speed , hits a smooth vertical wall surface elastically. Answer the following questions.

Just after the collision is over, the velocity of the lowest point of the ball is
, leftward
, leftward
, rightward
, rightward
The correct Answer is:B
Just after collision
Velocity of lowest potential
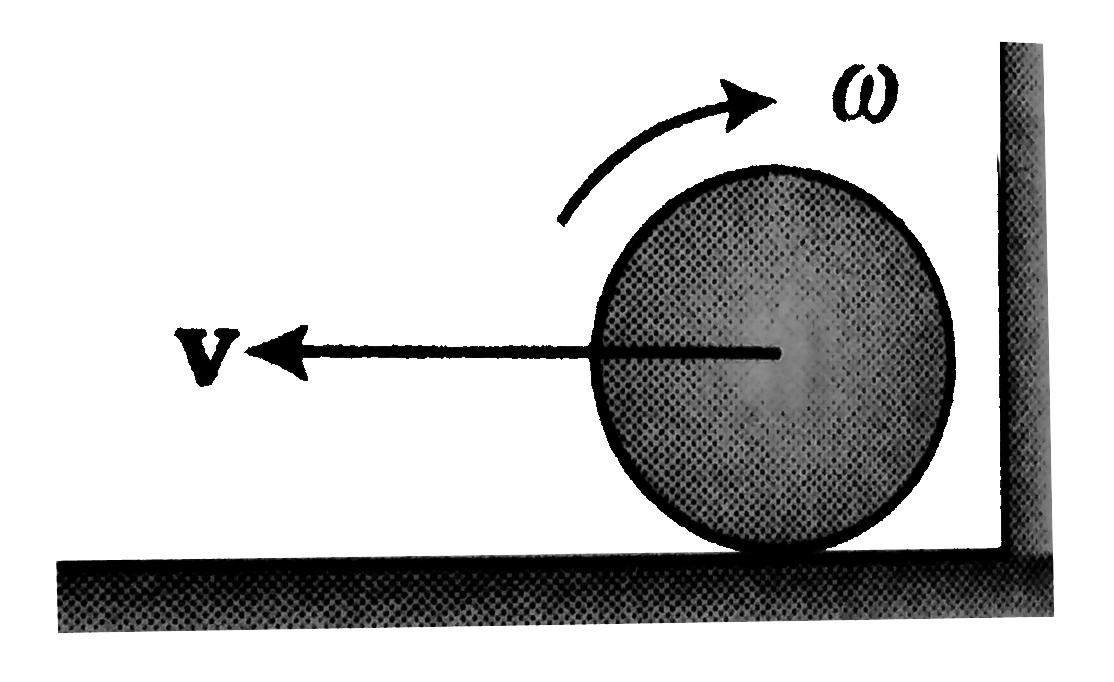
Change in angular momentum is due to translational part only, as does not change due to collision.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Integer7videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Fill In The Blanks7videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Multiple Correct26videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer11videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer16videos
SOUND WAVES AND DOPPLER EFFECT
Similar Questions
A ball, rolling purely on a horizontal floor with centre's speed v, hits a smooth vertical wall surface elastically. Answer the following questions.
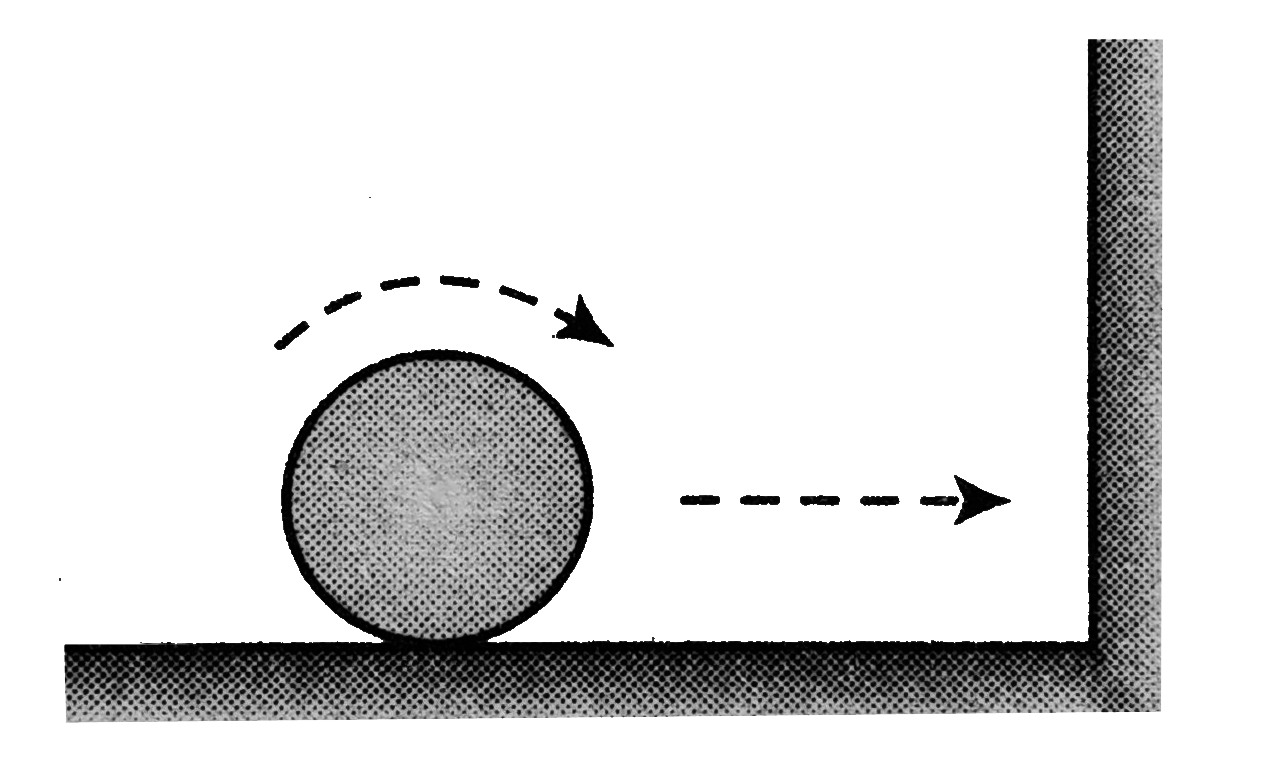
The change in angular momentum of the solid ball (mass m, radius R), about the corner point of floor and wall, due to the collision isView SolutionA sphere rolling on a horizontal rough surface Collides elastically with a smooth vertical wall, as shown in Fig. State which of the following statements is true or false.
 a. After collision, the velocity of the centre of mass gets reversed.
a. After collision, the velocity of the centre of mass gets reversed.
b. Angular momentum of the sphere about the point of contact with the wall is conserved.
c. Angular momentum of the sphere about a stationary point on the horizontal surface is conserved.
d. Just after collision the point of contact with the horizontal surface is moving towards the wall.
e. After collision the friction force acts on the sphere such that it decreases the linear speed and increases the angular speed.
f. Finally, when the sphere starts rolling, it is moving away from the wall.View SolutionA ball rolls without sliding over a rough horizontal floor with velocity v0=7m/s towards a smooth vertical wall. If coefficient of restitution between the wall and the ball is e=0.7. Calculate velocity v of the ball after the collision.
View SolutionTwo identical balls are rolling without slipping on a horizontal plane as shwon in figure. They undergo a perfect elastic collision. Just after collision, the velocity of image of the bottom point of A with respect to the plane mirros is x V, then x=
 View Solution
View SolutionA ball of radius R=20cm has mass m=0.75kg and moment of inertia (about its diameter ) I=0.0125kgm2. The ball rolls without sliding over a rough horizontal floor wilth velocity v0=10ms−1 towards a smooth vertical wall if coefficient of resutitution between the wall and the ball is e=0.7, calculate velocity v of the ball long after the collision. (g=10ms−2)
View SolutionA ball is projected on a very long floor. There may be two conditions (i) floor is smooth &(ii) the collision is elastic
If both the considered then the path of ball is as follows.

Now if collision is inelastic and surface is rough then the path is as follows.

Successive range is decreasing .
Roughness of surface decreases the horizontal component of ball during collision and inelastic nature of collision decreases the vertical component of velocity of ball. In first case both components remain unchanged in magnitude and in second case both the components of the velocity will change.
Let us consider a third case here surface is rough but the collision of ball with floor is elastic. A ball is projected withe speed u at an angle 30∘ with horizontal and it is known that after collision with the floor its speed becomes u√3 . Then answer the following questions.
If the ball after first collision with the floor has rebounded vertically then the speed of the ball just after the collision with the floor would have been :View SolutionA ball moving on a horizontal frictionless plane hits an identical ball at rest with a velocity of 0.5m/s. If the collision is elastic, calculate the speed imparted to the target ball, if the speed of projectile after the collision is 30cm/s.
View SolutionA uniform rod of mass M and length a lies on a smooth horizontal plane. A particle of mass m moving at a speed v perpendicular to the length of the rod strikes it at a distance a4 from the centre and stops after the collision. Find a. the velocity of the cente of the rod and b. the angular velocity of the rod abut its centre just after the collision.
View SolutionA glass ball collides with a smooth horizontal surface (xz plane) with a velocity V=ai−bj. If the coefficient of restitution of collision be e, the velocity of the ball just after the collision will be
View Solution
A stone is projected from a horizontal plane. It attains maximum height H & strikes a stationary smooth wall & falls on the ground vertically below the maximum height. Assuming the collision to be elastic the height of the point on the wall where ball will strike isView Solution
