A ball, rolling purely on a horizontal floor with centre's speed v, hits a smooth vertical wall surface elastically. Answer the following questions.
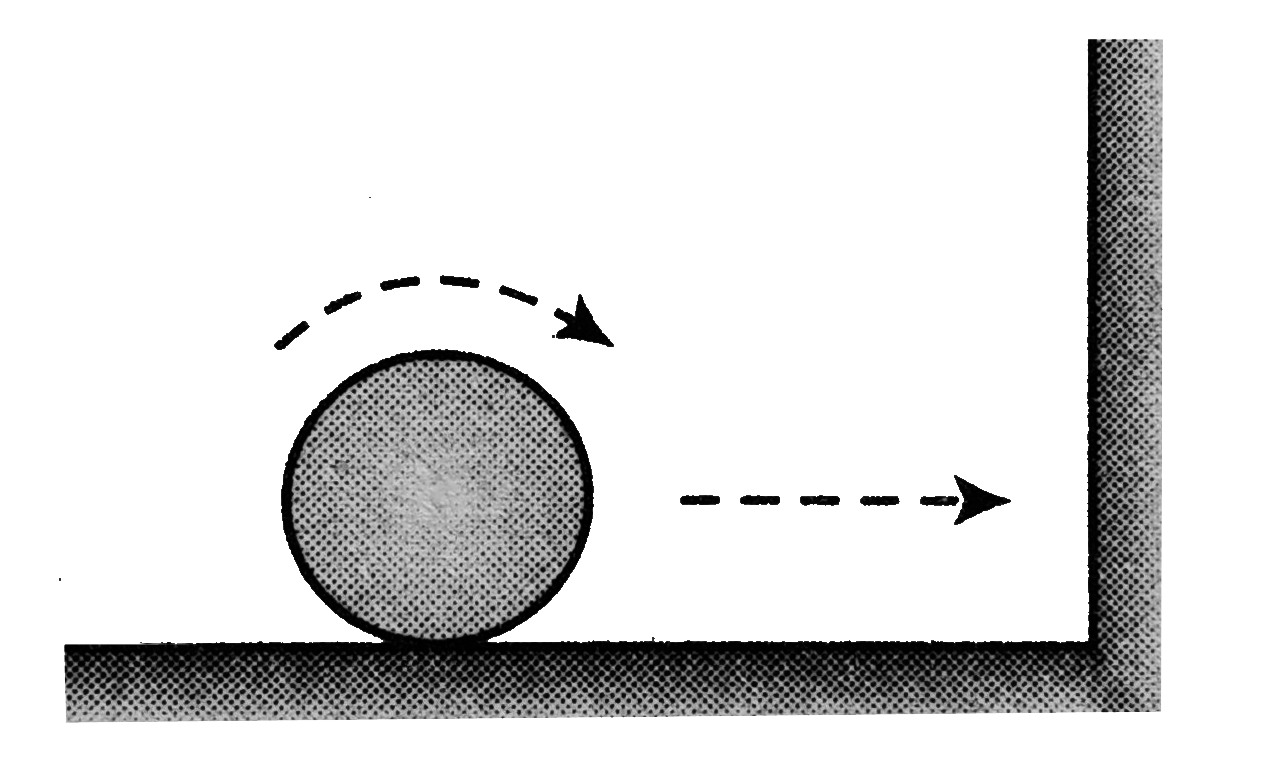
The change in angular momentum of the solid ball (mass m, radius R), about the corner point of floor and wall, due to the collision is
2mvR
mvR
mvR/2
none of these
The correct Answer is:A
Just after collision
v=ωr
Velocity of lowest potential =v+ωr=2v
Change in angular momentum is due to translational part only, as ω does not change due to collision.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Integer7videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Fill In The Blanks7videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Multiple Correct26videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer11videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer16videos
SOUND WAVES AND DOPPLER EFFECT
Similar Questions
A ball, rolling purely on a horizontal floor with centre's speed v, hits a smooth vertical wall surface elastically. Answer the following questions.
Just after the collision is over, the velocity of the lowest point of the ball isView SolutionA ball of mass m moving with velocity v, collide with the wall elastically as shown in the figure. After impact the change in angular momentum about P is :
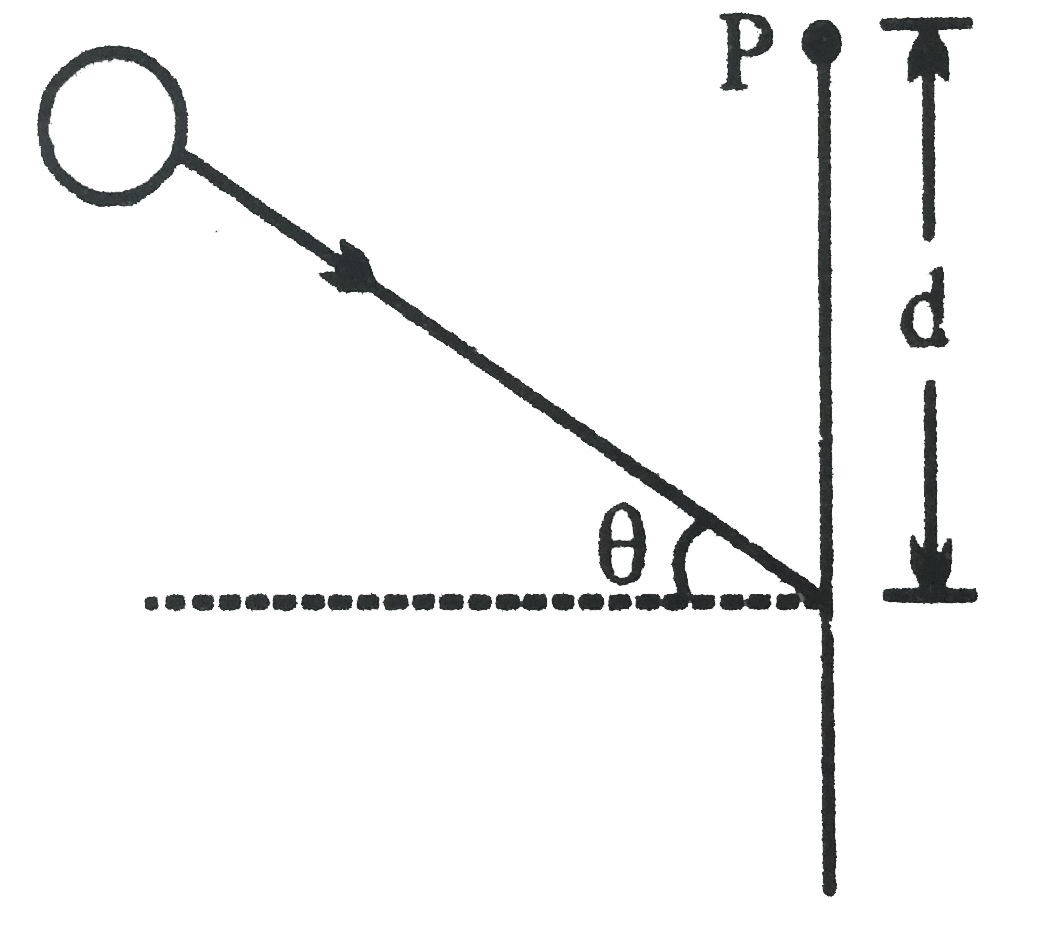.View SolutionA sphere rolling on a horizontal rough surface collides elastically with a smooth vertical wall, as shown in figure. During collision, angular momentum of the sphere is conserved about ____________. (Any point O on the surface/point of contact P)
View SolutionA ball rolls without sliding over a rough horizontal floor with velocity v0=7m/s towards a smooth vertical wall. If coefficient of restitution between the wall and the ball is e=0.7. Calculate velocity v of the ball after the collision.
View SolutionA sphere rolling on a horizontal rough surface Collides elastically with a smooth vertical wall, as shown in Fig. State which of the following statements is true or false.
a. After collision, the velocity of the centre of mass gets reversed.
b. Angular momentum of the sphere about the point of contact with the wall is conserved.
c. Angular momentum of the sphere about a stationary point on the horizontal surface is conserved.
d. Just after collision the point of contact with the horizontal surface is moving towards the wall.
e. After collision the friction force acts on the sphere such that it decreases the linear speed and increases the angular speed.
f. Finally, when the sphere starts rolling, it is moving away from the wall.View SolutionA ball of radius R=20cm has mass m=0.75kg and moment of inertia (about its diameter ) I=0.0125kgm2. The ball rolls without sliding over a rough horizontal floor wilth velocity v0=10ms−1 towards a smooth vertical wall if coefficient of resutitution between the wall and the ball is e=0.7, calculate velocity v of the ball long after the collision. (g=10ms−2)
View SolutionA particle of mass m strikes a wall with speed v at an angle 30∘ with the wall elastically as shown in the figure. The magnitude of impulse imparted to the ball by the wall is
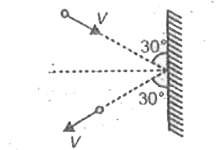
View Solution
A cicular disc of mass m and radius R is set into motion on a horizontal floor with a linear speed v in the forward direction and an angular speed ω=vR in clockwise direction as shown in figure. Find the magnitude of the total angular momentum of the disc about bottom most point O of the disc.View Solution-
A cicular disc of mass m and radius R is set into motion on a horizontal floor with a linear speed v in the forward direction and an angular speed ω=vR in clockwise direction as shown in figure. Find the magnitude of the total angular momentum of the disc about bottom most point O of the disc.View Solution A solid sphere rolls without slipping on a rough horizontal floor, moving with a speed v. It makes an elastic collision with a smooth vertical wall. After impact
View Solution